วิธีตรวจสอบว่าเวกเตอร์ขึ้นอยู่กับเชิงเส้นหรือไม่ การพึ่งพาเชิงเส้นและความเป็นอิสระเชิงเส้นของเวกเตอร์

ในการตรวจสอบว่าระบบของเวกเตอร์ขึ้นอยู่กับเชิงเส้นตรงหรือไม่ จำเป็นต้องเขียนผลรวมเชิงเส้นของเวกเตอร์เหล่านี้ และตรวจสอบว่าสามารถเป็นศูนย์ได้หรือไม่หากสัมประสิทธิ์อย่างน้อยหนึ่งค่าเท่ากับศูนย์

กรณีที่ 1 ระบบเวกเตอร์กำหนดโดยเวกเตอร์

การสร้างผลรวมเชิงเส้น

เราได้รับระบบสมการเอกพันธ์ ถ้ามีวิธีแก้ปัญหาที่ไม่ใช่ศูนย์ ดีเทอร์มีแนนต์จะต้องเท่ากับศูนย์ ลองเขียนดีเทอร์มิแนนต์และหาค่าของมันกัน

ดีเทอร์มีแนนต์เป็นศูนย์ ดังนั้นเวกเตอร์จึงขึ้นอยู่กับเชิงเส้นตรง

กรณีที่ 2 ระบบเวกเตอร์ถูกกำหนดโดยฟังก์ชันการวิเคราะห์:

ก)
ถ้าเอกลักษณ์เป็นจริง ระบบจะขึ้นอยู่กับเชิงเส้นตรง

มาสร้างผลรวมเชิงเส้นกัน

มีความจำเป็นต้องตรวจสอบว่ามี a, b, c อยู่หรือไม่ (อย่างน้อยหนึ่งรายการไม่เท่ากับศูนย์) ซึ่งนิพจน์นี้เท่ากับศูนย์

มาเขียนฟังก์ชันไฮเปอร์โบลิกกันดีกว่า

,
, แล้ว

จากนั้นผลรวมเชิงเส้นของเวกเตอร์จะอยู่ในรูปแบบ:

ที่ไหน
ตัวอย่างเช่น สมมุติว่าผลรวมเชิงเส้นเป็นศูนย์ ดังนั้น ระบบจึงขึ้นกับเชิงเส้นตรง

คำตอบ: ระบบจะขึ้นอยู่กับเชิงเส้นตรง

ข)
ลองสร้างผลรวมเชิงเส้นกัน

ผลรวมเชิงเส้นของเวกเตอร์จะต้องเท่ากับศูนย์สำหรับค่าใด ๆ ของ x

มาตรวจสอบกรณีพิเศษกัน

ผลรวมเชิงเส้นของเวกเตอร์จะเท่ากับศูนย์ก็ต่อเมื่อค่าสัมประสิทธิ์ทั้งหมดเท่ากับศูนย์

ดังนั้นระบบจึงเป็นอิสระเชิงเส้น

คำตอบ: ระบบมีความเป็นอิสระเชิงเส้น

5.3. ค้นหาพื้นฐานและกำหนดขนาดของพื้นที่โซลูชันเชิงเส้น

ลองสร้างเมทริกซ์แบบขยายและลดขนาดให้เป็นรูปสี่เหลี่ยมคางหมูโดยใช้วิธีเกาส์เซียน

เพื่อให้ได้พื้นฐานมาแทนที่ค่าที่กำหนดเอง:

เรามาพิกัดที่เหลือกันดีกว่า

คำตอบ:

5.4. ค้นหาพิกัดของเวกเตอร์ X บนพื้นฐาน หากระบุไว้ในฐาน

การค้นหาพิกัดเวกเตอร์ในรูปแบบใหม่นั้นเกี่ยวข้องกับการแก้ระบบสมการ

วิธีที่ 1 การค้นหาโดยใช้เมทริกซ์การเปลี่ยนแปลง

มาสร้างเมทริกซ์ทรานซิชันกันดีกว่า

ลองหาเวกเตอร์บนพื้นฐานใหม่โดยใช้สูตร

ลองหาเมทริกซ์ผกผันแล้วทำการคูณกัน

,

วิธีที่ 2 การค้นหาโดยการเขียนระบบสมการ

ลองเขียนเวกเตอร์พื้นฐานจากค่าสัมประสิทธิ์พื้นฐานกัน

,
,

การค้นหาเวกเตอร์บนพื้นฐานใหม่จะมีรูปแบบ

, ที่ไหน งนี่คือเวกเตอร์ที่กำหนด x.

สมการผลลัพธ์สามารถแก้ไขได้ด้วยวิธีใดคำตอบจะคล้ายกัน

คำตอบ: เวกเตอร์ในรูปแบบใหม่
.

5.5. ให้ x = (x 1 , x 2 , x 3 ) . การแปลงต่อไปนี้เป็นเส้นตรงหรือไม่?

ลองเขียนเมทริกซ์ของตัวดำเนินการเชิงเส้นจากสัมประสิทธิ์ของเวกเตอร์ที่กำหนดกัน

ลองตรวจสอบคุณสมบัติของการดำเนินการเชิงเส้นสำหรับเมทริกซ์ตัวดำเนินการเชิงเส้นแต่ละตัว

เราหาด้านซ้ายโดยการคูณเมทริกซ์ กเป็นเวกเตอร์

เราค้นหาด้านขวาโดยการคูณเวกเตอร์ที่กำหนดด้วยสเกลาร์
.

เราเห็นสิ่งนั้น
ซึ่งหมายความว่าการแปลงไม่เป็นเชิงเส้น

ลองตรวจสอบเวกเตอร์อื่นกัน

, การแปลงไม่เป็นเชิงเส้น

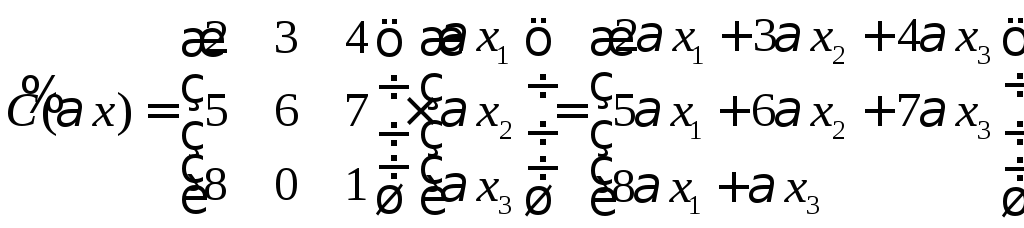
, การแปลงเป็นเส้นตรง

คำตอบ: โอ้– ไม่ใช่การแปลงเชิงเส้น ใน– ไม่เป็นเส้นตรง Cx– เชิงเส้น

บันทึก.คุณสามารถทำงานนี้ให้สำเร็จได้ง่ายขึ้นมากโดยดูเวกเตอร์ที่ให้มาอย่างระมัดระวัง ใน โอ้เราเห็นว่ามีคำศัพท์ที่ไม่มีองค์ประกอบอยู่ เอ็กซ์ซึ่งไม่สามารถรับได้เนื่องจากการดำเนินการเชิงเส้น ใน ในมีองค์ประกอบอยู่ เอ็กซ์ยกกำลังสาม ซึ่งไม่สามารถหาได้จากการคูณด้วยเวกเตอร์ เอ็กซ์.

5.6. ที่ให้ไว้ x = { x 1 , x 2 , x 3 } , ขวาน = { x 2 – x 3 , x 1 , x 1 + x 3 } , บีเอ็กซ์ = { x 2 , 2 x 3 , x 1 } . ดำเนินการตามที่ระบุ: ( ก ( บี – ก )) x .

ให้เราเขียนเมทริกซ์ของตัวดำเนินการเชิงเส้น

เรามาดำเนินการกับเมทริกซ์กัน

เมื่อคูณเมทริกซ์ผลลัพธ์ด้วย X เราจะได้

คำตอบ:

เวกเตอร์ คุณสมบัติ และการกระทำกับเวกเตอร์

เวกเตอร์ การกระทำกับเวกเตอร์ สเปซเวกเตอร์เชิงเส้น

เวกเตอร์คือชุดรวมของจำนวนจริงที่มีจำนวนจำกัดตามลำดับ

การดำเนินการ: 1. การคูณเวกเตอร์ด้วยตัวเลข: lambda*vector x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3.4, 0, 7)*3=(9, 12,0.21)

2. การบวกเวกเตอร์ (อยู่ในปริภูมิเวกเตอร์เดียวกัน) เวกเตอร์ x + เวกเตอร์ y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. เวกเตอร์ 0=(0,0…0)---n E n – n มิติ (ปริภูมิเชิงเส้น) เวกเตอร์ x + เวกเตอร์ 0 = เวกเตอร์ x

ทฤษฎีบท. เพื่อให้ระบบของเวกเตอร์ n ซึ่งเป็นปริภูมิเชิงเส้น n มิติ เป็นอิสระเชิงเส้น จำเป็นและเพียงพอที่เวกเตอร์ตัวใดตัวหนึ่งจะต้องเป็นผลรวมเชิงเส้นของเวกเตอร์ตัวอื่น

ทฤษฎีบท. เซตของเวกเตอร์ลำดับที่ 1 จำนวน n+ ใดๆ ของปริภูมิเชิงเส้น n มิติของปรากฏการณ์ ขึ้นอยู่กับเชิงเส้น

การบวกเวกเตอร์ การคูณเวกเตอร์ด้วยตัวเลข การลบเวกเตอร์

ผลรวมของเวกเตอร์สองตัวคือเวกเตอร์ที่ลากจากจุดเริ่มต้นของเวกเตอร์ไปยังจุดสิ้นสุดของเวกเตอร์ โดยมีเงื่อนไขว่าจุดเริ่มต้นจะต้องตรงกับจุดสิ้นสุดของเวกเตอร์ หากเวกเตอร์ถูกกำหนดโดยการขยายในเวกเตอร์หน่วยพื้นฐาน จากนั้นเมื่อเพิ่มเวกเตอร์ พิกัดที่สอดคล้องกันจะถูกเพิ่มเข้าไป

ลองพิจารณาเรื่องนี้โดยใช้ตัวอย่างของระบบพิกัดคาร์ทีเซียน อนุญาต

มาแสดงกันเถอะ

จากภาพที่ 3 ชัดเจนว่า

ผลรวมของเวกเตอร์จำนวนจำกัดใดๆ สามารถพบได้โดยใช้กฎรูปหลายเหลี่ยม (รูปที่ 4): เพื่อสร้างผลรวมของเวกเตอร์จำนวนจำกัด ก็เพียงพอที่จะรวมจุดเริ่มต้นของเวกเตอร์ที่ตามมาแต่ละตัวเข้ากับจุดสิ้นสุดของเวกเตอร์ก่อนหน้า และสร้างเวกเตอร์ที่เชื่อมต่อจุดเริ่มต้นของเวกเตอร์แรกกับจุดสิ้นสุดของเวกเตอร์สุดท้าย

คุณสมบัติของการดำเนินการบวกเวกเตอร์:

ในนิพจน์เหล่านี้ m, n คือตัวเลข

ความแตกต่างระหว่างเวกเตอร์เรียกว่าเวกเตอร์ เทอมที่สองคือเวกเตอร์ที่อยู่ตรงข้ามกับเวกเตอร์ในทิศทางแต่มีความยาวเท่ากับเวกเตอร์

ดังนั้นการดำเนินการลบเวกเตอร์จึงถูกแทนที่ด้วยการดำเนินการบวก

เวกเตอร์ที่มีจุดเริ่มต้นอยู่ที่จุดกำเนิดและสิ้นสุดที่จุด A (x1, y1, z1) เรียกว่าเวกเตอร์รัศมีของจุด A และเขียนแทนง่ายๆ เนื่องจากพิกัดของมันตรงกับพิกัดของจุด A การขยายตัวในหน่วยเวกเตอร์จึงมีรูปแบบ

เวกเตอร์ที่เริ่มต้นที่จุด A(x1, y1, z1) และสิ้นสุดที่จุด B(x2, y2, z2) สามารถเขียนได้เป็น

โดยที่ r 2 คือเวกเตอร์รัศมีของจุด B; r 1 - เวกเตอร์รัศมีของจุด A

ดังนั้นการขยายตัวของเวกเตอร์ในหน่วยเวกเตอร์จึงมีรูปแบบ

ความยาวเท่ากับระยะห่างระหว่างจุด A และ B

การคูณ

ดังนั้นในกรณีที่เกิดปัญหาระนาบ ผลคูณของเวกเตอร์โดย a = (ax; ay) คูณจำนวน b จะถูกหาได้จากสูตร

a b = (ขวาน b; ay b)

ตัวอย่างที่ 1 ค้นหาผลคูณของเวกเตอร์ a = (1; 2) คูณ 3

3 ก = (3 1; 3 2) = (3; 6)

ดังนั้น ในกรณีที่เกิดปัญหาเชิงพื้นที่ ผลคูณของเวกเตอร์ a = (ax; ay; az) ตามจำนวน b จะพบได้จากสูตร

a b = (ขวาน b; ay b; az b)

ตัวอย่างที่ 1 ค้นหาผลคูณของเวกเตอร์ a = (1; 2; -5) คูณ 2

2 ก = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

ผลคูณดอทของเวกเตอร์และ มุมระหว่างเวกเตอร์และอยู่ที่ไหน ; ถ้าอย่างใดอย่างหนึ่งแล้ว

จากคำจำกัดความของผลิตภัณฑ์สเกลาร์จะได้ดังนี้

โดยที่ ตัวอย่างเช่น คือขนาดของเส้นโครงของเวกเตอร์ไปยังทิศทางของเวกเตอร์

เวกเตอร์กำลังสองแบบสเกลาร์:

คุณสมบัติของผลิตภัณฑ์ดอท:

สินค้าดอทในพิกัด

ถ้า ที่

มุมระหว่างเวกเตอร์

มุมระหว่างเวกเตอร์ - มุมระหว่างทิศทางของเวกเตอร์เหล่านี้ (มุมที่เล็กที่สุด)

ครอสโปรดัค (ครอสโปรดัคของเวกเตอร์สองตัว) -นี่เป็นเวกเตอร์เทียมที่ตั้งฉากกับระนาบที่สร้างจากปัจจัยสองประการ ซึ่งเป็นผลมาจากการดำเนินการไบนารี่ "การคูณเวกเตอร์" บนเวกเตอร์ในปริภูมิยูคลิดสามมิติ ผลคูณไม่สามารถสับเปลี่ยนหรือเชื่อมโยงได้ (เป็นสารต้านสับเปลี่ยน) และแตกต่างจากผลคูณดอทของเวกเตอร์ ในปัญหาทางวิศวกรรมและฟิสิกส์หลายๆ อย่าง คุณจะต้องสามารถสร้างเวกเตอร์ที่ตั้งฉากกับเวกเตอร์ที่มีอยู่สองตัวได้ - ผลคูณของเวกเตอร์ให้โอกาสนี้ ผลคูณไขว้มีประโยชน์สำหรับ "การวัด" เส้นตั้งฉากของเวกเตอร์ - ความยาวของผลคูณไขว้ของเวกเตอร์สองตัวจะเท่ากับผลคูณของความยาวหากพวกมันตั้งฉากกัน และจะลดลงเหลือศูนย์หากเวกเตอร์ขนานกันหรือขนานกัน

ผลคูณไขว้ถูกกำหนดไว้เฉพาะในช่องว่างสามมิติและเจ็ดมิติเท่านั้น ผลลัพธ์ของผลิตภัณฑ์เวกเตอร์ เช่นเดียวกับผลคูณสเกลาร์ ขึ้นอยู่กับหน่วยเมตริกของปริภูมิแบบยุคลิด

ต่างจากสูตรในการคำนวณเวกเตอร์ผลคูณสเกลาร์จากพิกัดในระบบพิกัดสี่เหลี่ยมสามมิติ สูตรสำหรับผลคูณไขว้นั้นขึ้นอยู่กับการวางแนวของระบบพิกัดสี่เหลี่ยมหรือกล่าวอีกนัยหนึ่งคือ "chirality"

เส้นตรงของเวกเตอร์

เวกเตอร์ที่ไม่ใช่ศูนย์ (ไม่เท่ากับ 0) สองตัวจะถูกเรียกว่าคอลลิเนียร์หากพวกมันอยู่บนเส้นคู่ขนานหรืออยู่บนเส้นเดียวกัน คำพ้องความหมายที่ยอมรับได้ แต่ไม่แนะนำคือเวกเตอร์ "ขนาน" เวกเตอร์คอลลิเนียร์สามารถมีทิศทางที่เหมือนกัน ("โคไดนามิก") หรือทิศทางตรงกันข้าม (ในกรณีหลังบางครั้งเรียกว่า "แอนติคอลลิเนียร์" หรือ "แอนติขนาน")

ผลคูณผสมของเวกเตอร์( ก ข ค)- ผลคูณสเกลาร์ของเวกเตอร์ a และผลิตภัณฑ์เวกเตอร์ของเวกเตอร์ b และ c:

(a,b,c)=a ⋅(b ×c)

บางครั้งเรียกว่าสามเท่า ผลิตภัณฑ์สเกลาร์เวกเตอร์ น่าจะเนื่องมาจากข้อเท็จจริงที่ว่าผลลัพธ์เป็นสเกลาร์ (แม่นยำกว่านั้นคือ pseudoscalar)

ความหมายทางเรขาคณิต: โมดูลัสของผลิตภัณฑ์ผสมจะมีค่าเท่ากับตัวเลขของปริมาตรของเส้นขนานที่เกิดจากเวกเตอร์ (ก,ข,ค) .

คุณสมบัติ

ผลิตภัณฑ์แบบผสมมีความเบ้สมมาตรโดยคำนึงถึงข้อโต้แย้งทั้งหมด: กล่าวคือ จ. การจัดเรียงปัจจัยสองประการใหม่จะเปลี่ยนเครื่องหมายของผลิตภัณฑ์ ผลคูณผสมในระบบพิกัดคาร์ทีเซียนด้านขวา (ในรูปแบบออร์โธนอร์มอล) เท่ากับดีเทอร์มิแนนต์ของเมทริกซ์ที่ประกอบด้วยเวกเตอร์ และ:

ผลคูณผสมในระบบพิกัดคาร์ทีเซียนด้านซ้าย (ในรูปแบบออร์โธนอร์มอล) เท่ากับดีเทอร์มิแนนต์ของเมทริกซ์ที่ประกอบด้วยเวกเตอร์ และนำมาด้วยเครื่องหมายลบ:

โดยเฉพาะอย่างยิ่ง,

ถ้าเวกเตอร์สองตัวใดขนานกัน แล้วเวกเตอร์ตัวที่สามจะเกิดผลคูณผสมเท่ากับศูนย์

หากเวกเตอร์สามตัวขึ้นอยู่กับเชิงเส้นตรง (นั่นคือ coplanar อยู่ในระนาบเดียวกัน) ผลคูณที่ผสมกันจะเท่ากับศูนย์

ความหมายทางเรขาคณิต - ผลคูณผสมมีค่าเท่ากันในค่าสัมบูรณ์กับปริมาตรของเส้นขนาน (ดูรูป) ที่เกิดจากเวกเตอร์และ เครื่องหมายขึ้นอยู่กับว่าเวกเตอร์ทั้งสามนี้ถนัดขวาหรือถนัดซ้าย

ระนาบร่วมของเวกเตอร์

เวกเตอร์สามตัว (หรือมากกว่า) เรียกว่า coplanar ถ้าพวกมันถูกลดขนาดลงสู่จุดกำเนิดร่วมและอยู่ในระนาบเดียวกัน

คุณสมบัติของระนาบร่วม

ถ้าอย่างน้อยหนึ่งในสามเวกเตอร์เป็นศูนย์ แล้วเวกเตอร์ทั้งสามนั้นก็ถูกพิจารณาว่าเป็นระนาบเดียวกัน

เวกเตอร์สามตัวที่มีเวกเตอร์คอลลิเนียร์คู่หนึ่งคือโคพลานาร์

ผลคูณผสมของเวกเตอร์โคพลานาร์ นี่คือเกณฑ์สำหรับ coplanarity ของเวกเตอร์สามตัว

เวกเตอร์โคพลานาร์นั้นขึ้นอยู่กับเชิงเส้นตรง นี่เป็นเกณฑ์สำหรับการทำงานร่วมกันด้วย

ในปริภูมิ 3 มิติ เวกเตอร์ที่ไม่ใช่ระนาบเดียวกัน 3 ตัวจะก่อตัวเป็นพื้นฐาน

เวกเตอร์ขึ้นอยู่กับเชิงเส้นและเวกเตอร์อิสระเชิงเส้น

ระบบเวกเตอร์ขึ้นอยู่กับเชิงเส้นและเป็นอิสระคำนิยาม. เรียกว่าระบบเวกเตอร์ ขึ้นอยู่กับเชิงเส้นถ้ามีผลรวมเชิงเส้นที่ไม่ไม่สำคัญอย่างน้อยหนึ่งตัวของเวกเตอร์เหล่านี้ ซึ่งเท่ากับเวกเตอร์ศูนย์ มิฉะนั้นนั่นคือ หากเพียงผลรวมเชิงเส้นเล็กน้อยของเวกเตอร์ที่กำหนดเท่านั้นที่เท่ากับเวกเตอร์ว่าง เวกเตอร์จะถูกเรียก เป็นอิสระเชิงเส้น.

ทฤษฎีบท (เกณฑ์การพึ่งพาเชิงเส้น). เพื่อให้ระบบของเวกเตอร์ในปริภูมิเชิงเส้นเป็นอิสระเชิงเส้น จำเป็นและเพียงพอที่เวกเตอร์เหล่านี้อย่างน้อยหนึ่งตัวจะเป็นผลรวมเชิงเส้นของเวกเตอร์อื่นๆ

1) หากในบรรดาเวกเตอร์มีเวกเตอร์ศูนย์อย่างน้อยหนึ่งตัว ระบบเวกเตอร์ทั้งหมดจะขึ้นอยู่กับเชิงเส้นตรง

ในความเป็นจริง ตัวอย่างเช่น หาก สมมุติว่า เรามีผลรวมเชิงเส้นที่ไม่สำคัญ ▲

2) ถ้าในบรรดาเวกเตอร์บางรูปแบบเป็นระบบที่ขึ้นอยู่กับเชิงเส้น ดังนั้นทั้งระบบก็จะขึ้นอยู่กับเชิงเส้นตรง

แท้จริงแล้ว ให้เวกเตอร์ , , เป็นอิสระเชิงเส้น ซึ่งหมายความว่ามีการรวมกันเชิงเส้นที่ไม่สำคัญเท่ากับเวกเตอร์ศูนย์ แต่แล้วสมมุติว่า เรายังได้รับผลรวมเชิงเส้นที่ไม่ไม่สำคัญเท่ากับเวกเตอร์ศูนย์ด้วย

2. พื้นฐานและมิติ คำนิยาม. ระบบเวกเตอร์อิสระเชิงเส้น เรียกว่าปริภูมิเวกเตอร์ พื้นฐานของปริภูมินี้หากเวกเตอร์ใดๆ สามารถแสดงเป็นผลรวมเชิงเส้นของเวกเตอร์ของระบบนี้ กล่าวคือ สำหรับเวกเตอร์แต่ละตัวจะมีจำนวนจริง จนมีความเสมอภาคคงอยู่ ความเสมอภาค นี้เรียกว่า การสลายตัวของเวกเตอร์ตามพื้นฐานและตัวเลข ถูกเรียก พิกัดของเวกเตอร์สัมพันธ์กับฐาน(หรือ ในพื้นฐาน) .

ทฤษฎีบท (บนเอกลักษณ์ของการขยายตัวโดยคำนึงถึงพื้นฐาน). เวกเตอร์ทุกตัวในอวกาศสามารถขยายเป็นฐานได้ ในทางเดียวนั่นคือ พิกัดของเวกเตอร์แต่ละตัวบนพื้นฐาน ถูกกำหนดไว้อย่างไม่คลุมเครือ

ภารกิจที่ 1ค้นหาว่าระบบเวกเตอร์มีความเป็นอิสระเชิงเส้นหรือไม่ ระบบของเวกเตอร์จะถูกระบุโดยเมทริกซ์ของระบบ ซึ่งคอลัมน์ประกอบด้วยพิกัดของเวกเตอร์

.

สารละลาย.ปล่อยให้ผลรวมเชิงเส้น เท่ากับศูนย์ เมื่อเขียนความเท่าเทียมกันนี้ในพิกัดแล้ว เราจะได้ระบบสมการต่อไปนี้:

.

ระบบสมการดังกล่าวเรียกว่าสามเหลี่ยม เธอมีทางออกเดียวเท่านั้น . ดังนั้นเวกเตอร์ เป็นอิสระเชิงเส้น

ภารกิจที่ 2ค้นหาว่าระบบเวกเตอร์มีความเป็นอิสระเชิงเส้นหรือไม่

.

สารละลาย.เวกเตอร์ เป็นอิสระเชิงเส้น (ดูปัญหาที่ 1) ให้เราพิสูจน์ว่าเวกเตอร์คือผลรวมเชิงเส้นของเวกเตอร์ . สัมประสิทธิ์การขยายตัวของเวกเตอร์ ถูกกำหนดจากระบบสมการ

.

ระบบนี้มีวิธีแก้ปัญหาเฉพาะตัวเช่นเดียวกับระบบสามเหลี่ยม

ดังนั้นระบบเวกเตอร์ ขึ้นอยู่กับเชิงเส้น

ความคิดเห็น. เมทริกซ์ชนิดเดียวกันกับในปัญหาที่ 1 เรียกว่า สามเหลี่ยม และในปัญหาที่ 2 – ก้าวเป็นรูปสามเหลี่ยม . คำถามเกี่ยวกับการพึ่งพาเชิงเส้นของระบบเวกเตอร์นั้นแก้ไขได้ง่ายถ้าเมทริกซ์ที่ประกอบด้วยพิกัดของเวกเตอร์เหล่านี้เป็นสามเหลี่ยมขั้น หากเมทริกซ์ไม่มีรูปแบบพิเศษให้ใช้ การแปลงสตริงเบื้องต้น เพื่อรักษาความสัมพันธ์เชิงเส้นระหว่างคอลัมน์ จึงสามารถลดให้เป็นรูปแบบสามเหลี่ยมขั้นบันไดได้

การแปลงสตริงเบื้องต้นเมทริกซ์ (EPS) การดำเนินการต่อไปนี้บนเมทริกซ์เรียกว่า:

1) การจัดเรียงบรรทัดใหม่

2) การคูณสตริงด้วยตัวเลขที่ไม่ใช่ศูนย์

3) เพิ่มสตริงอื่นลงในสตริงคูณด้วยตัวเลขใดก็ได้

ภารกิจที่ 3ค้นหาระบบย่อยอิสระเชิงเส้นสูงสุดและคำนวณอันดับของระบบเวกเตอร์

.

สารละลาย.ให้เราลดเมทริกซ์ของระบบโดยใช้ EPS ให้เป็นรูปแบบสามเหลี่ยมขั้นบันได เพื่ออธิบายขั้นตอนนี้ เราแสดงบรรทัดที่มีจำนวนเมทริกซ์ที่จะแปลงด้วยสัญลักษณ์ คอลัมน์หลังลูกศรระบุการดำเนินการในแถวของเมทริกซ์ที่กำลังแปลงซึ่งจะต้องดำเนินการเพื่อให้ได้แถวของเมทริกซ์ใหม่

.

แน่นอนว่าสองคอลัมน์แรกของเมทริกซ์ผลลัพธ์มีความเป็นอิสระเชิงเส้น คอลัมน์ที่สามคือผลรวมเชิงเส้น และคอลัมน์ที่สี่ไม่ได้ขึ้นอยู่กับสองคอลัมน์แรก เวกเตอร์ เรียกว่าพื้นฐาน พวกมันสร้างระบบย่อยที่เป็นอิสระเชิงเส้นสูงสุดของระบบ และอันดับของระบบคือสาม

พื้นฐานพิกัด

ภารกิจที่ 4ค้นหาพื้นฐานและพิกัดของเวกเตอร์บนพื้นฐานนี้จากเซตของเวกเตอร์เชิงเรขาคณิตซึ่งมีพิกัดที่ตรงตามเงื่อนไข .

สารละลาย. ฉากนี้เป็นเครื่องบินที่ผ่านจุดกำเนิด พื้นฐานตามอำเภอใจบนระนาบประกอบด้วยเวกเตอร์ที่ไม่ใช่คอลลิเนียร์สองตัว พิกัดของเวกเตอร์บนพื้นฐานที่เลือกถูกกำหนดโดยการแก้ระบบสมการเชิงเส้นที่สอดคล้องกัน

มีอีกวิธีหนึ่งในการแก้ปัญหานี้ เมื่อคุณสามารถค้นหาฐานโดยใช้พิกัดได้

พิกัด ช่องว่างไม่ใช่พิกัดบนระนาบ เนื่องจากมีความสัมพันธ์กันด้วยความสัมพันธ์ นั่นคือพวกเขาไม่เป็นอิสระ ตัวแปรอิสระและ (เรียกว่าอิสระ) จะกำหนดเวกเตอร์บนระนาบโดยไม่ซ้ำกัน ดังนั้นจึงสามารถเลือกเป็นพิกัดใน แล้วพื้นฐาน ประกอบด้วยเวกเตอร์ที่อยู่ในและสอดคล้องกับเซตของตัวแปรอิสระ และ , นั่นคือ .

ภารกิจที่ 5ค้นหาฐานและพิกัดของเวกเตอร์บนพื้นฐานนี้จากเซตของเวกเตอร์ทั้งหมดในอวกาศซึ่งมีพิกัดคี่เท่ากัน

สารละลาย. ให้เราเลือกพิกัดในอวกาศเช่นเดียวกับในปัญหาที่แล้ว

เพราะ แล้วตามด้วยตัวแปรอิสระ กำหนดเวกเตอร์โดยไม่ซ้ำกันจากและเป็นพิกัด พื้นฐานที่เกี่ยวข้องประกอบด้วยเวกเตอร์

ภารกิจที่ 6ค้นหาพื้นฐานและพิกัดของเวกเตอร์บนพื้นฐานนี้จากเซตของเมทริกซ์ทั้งหมดในแบบฟอร์ม , ที่ไหน – ตัวเลขที่กำหนดเอง

สารละลาย. เมทริกซ์แต่ละตัวจากสามารถแสดงได้ไม่ซ้ำกันในรูปแบบ:

ความสัมพันธ์นี้คือการขยายตัวของเวกเตอร์จากเทียบกับพื้นฐาน
พร้อมพิกัด .

ภารกิจที่ 7ค้นหามิติและพื้นฐานของเส้นตรงของระบบเวกเตอร์

.

สารละลาย.เมื่อใช้ EPS เราจะแปลงเมทริกซ์จากพิกัดของเวกเตอร์ของระบบเป็นรูปแบบสามเหลี่ยมขั้นบันได

.

คอลัมน์ เมทริกซ์สุดท้ายมีความเป็นอิสระเชิงเส้นและคอลัมน์ แสดงเป็นเส้นตรงผ่านพวกมัน ดังนั้นเวกเตอร์ เป็นพื้นฐาน , และ .

ความคิดเห็น. พื้นฐานใน ถูกเลือกอย่างคลุมเครือ ตัวอย่างเช่น เวกเตอร์ มาเป็นพื้นฐานด้วย .

ในบทความนี้เราจะกล่าวถึง:

• เวกเตอร์คอลลิเนียร์คืออะไร
• อะไรคือเงื่อนไขสำหรับความเป็นเส้นตรงของเวกเตอร์
• คุณสมบัติของเวกเตอร์คอลลิเนียร์คืออะไร
• การพึ่งพาเชิงเส้นของเวกเตอร์คอลลิเนียร์คืออะไร

Yandex.RTB R-A-339285-1 คำจำกัดความ 1

เวกเตอร์คอลลิเนียร์คือเวกเตอร์ที่ขนานกับเส้นตรงหรืออยู่บนเส้นเดียว

ตัวอย่างที่ 1

เงื่อนไขสำหรับการคอลลิเนียร์ริตีของเวกเตอร์

เวกเตอร์สองตัวจะขนานกันหากมีเงื่อนไขใด ๆ ต่อไปนี้เป็นจริง:

• เงื่อนไข 1 . เวกเตอร์ a และ b อยู่ในแนวเดียวกันถ้ามีจำนวน γ โดยที่ a = แล b;
• เงื่อนไข 2 . เวกเตอร์ a และ b อยู่ในแนวเดียวกันโดยมีอัตราส่วนพิกัดเท่ากัน:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• เงื่อนไข 3 . เวกเตอร์ a และ b เป็นเส้นตรงโดยมีเงื่อนไขว่าผลคูณไขว้และเวกเตอร์ศูนย์เท่ากัน:

ก ∥ ข ⇔ ก, ข = 0

หมายเหตุ 1

เงื่อนไขที่ 2 ใช้ไม่ได้หากพิกัดเวกเตอร์ตัวใดตัวหนึ่งเป็นศูนย์

โน้ต 2

เงื่อนไขที่ 3 ใช้เฉพาะกับเวกเตอร์ที่ระบุในช่องว่างเท่านั้น

ตัวอย่างปัญหาเพื่อศึกษาความเป็นเส้นตรงของเวกเตอร์

ตัวอย่างที่ 1

เราตรวจสอบเวกเตอร์ a = (1; 3) และ b = (2; 1) เพื่อหาความเป็นเชิงเส้น

วิธีแก้ปัญหา?

ในกรณีนี้ จำเป็นต้องใช้เงื่อนไขคอลลิเนียร์ริตีที่ 2 สำหรับเวกเตอร์ที่กำหนดจะมีลักษณะดังนี้:

ความเท่าเทียมกันเป็นเท็จ จากนี้เราสามารถสรุปได้ว่าเวกเตอร์ a และ b ไม่ใช่เส้นตรง

คำตอบ : ก | | ข

ตัวอย่างที่ 2

ค่า m ของเวกเตอร์ a = (1; 2) และ b = (- 1; m) จำเป็นสำหรับเวกเตอร์ที่จะอยู่ในแนวเดียวกัน?

วิธีแก้ปัญหา?

เมื่อใช้เงื่อนไขคอลลิเนียร์ริตีที่สอง เวกเตอร์จะอยู่ในแนวเดียวกันหากพิกัดของพวกมันเป็นสัดส่วน:

นี่แสดงว่า m = - 2

คำตอบ: ม. = - 2 .

เกณฑ์สำหรับการพึ่งพาเชิงเส้นและความเป็นอิสระเชิงเส้นของระบบเวกเตอร์

ทฤษฎีบท

ระบบเวกเตอร์ในปริภูมิเวกเตอร์จะขึ้นอยู่กับเชิงเส้นตรงก็ต่อเมื่อเวกเตอร์ตัวใดตัวหนึ่งของระบบสามารถแสดงในรูปของเวกเตอร์ที่เหลืออยู่ของระบบนี้

การพิสูจน์

ให้ระบบ e 1 , e 2 , . . . , e n ขึ้นอยู่กับเชิงเส้น ให้เราเขียนผลรวมเชิงเส้นของระบบนี้เท่ากับเวกเตอร์ศูนย์:

ก 1 อี 1 + 2 อี 2 + . . . + a และ e n = 0

โดยที่ค่าสัมประสิทธิ์การรวมกันอย่างน้อยหนึ่งค่าไม่เท่ากับศูนย์

ให้ k ≠ 0 k ∈ 1 , 2 , . . . , n.

เราหารทั้งสองด้านของความเท่าเทียมกันด้วยสัมประสิทธิ์ที่ไม่เป็นศูนย์:

ak - 1 (ak - 1 a 1) e 1 + (ak - 1 a k) e k + . . . + (a k - 1 n) e n = 0

เรามาแสดงว่า:

A k - 1 a m โดยที่ m ∈ 1 , 2 , . . . , เค - 1 , เค + 1 , น

ในกรณีนี้:

β 1 อี 1 + . . . + β k - 1 ek - 1 + β k + 1 ek + 1 + . . . + β n อี n = 0

หรือ e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) อี น

ตามมาว่าหนึ่งในเวกเตอร์ของระบบแสดงผ่านเวกเตอร์อื่นๆ ทั้งหมดของระบบ ซึ่งเป็นสิ่งที่ต้องพิสูจน์ (ฯลฯ )

ความเพียงพอ

ให้เวกเตอร์ตัวใดตัวหนึ่งแสดงเป็นเส้นตรงผ่านเวกเตอร์อื่นๆ ทั้งหมดของระบบ:

อีเค = γ 1 อี 1 + . . . + γ k - 1 ek - 1 + γ k + 1 ek + 1 + . . . + γ n อี n

เราย้ายเวกเตอร์ e k ไปทางด้านขวาของความเท่าเทียมกันนี้:

0 = γ 1 อี 1 + . . . + γ k - 1 ek - 1 - ek + γ k + 1 ek + 1 + . . . + γ n อี n

เนื่องจากสัมประสิทธิ์ของเวกเตอร์ e k เท่ากับ - 1 ≠ 0 เราจึงได้ค่าศูนย์ที่ไม่สำคัญโดยระบบเวกเตอร์ e 1, e 2, . . , e n และนี่ก็หมายความว่าอย่างนั้น ระบบนี้เวกเตอร์นั้นขึ้นอยู่กับเชิงเส้นตรง ซึ่งเป็นสิ่งที่ต้องพิสูจน์ (ฯลฯ )

ผลที่ตามมา:

• ระบบของเวกเตอร์มีความเป็นอิสระเชิงเส้น เมื่อไม่สามารถแสดงเวกเตอร์ใดๆ ของมันในรูปของเวกเตอร์อื่นๆ ทั้งหมดของระบบได้
• ระบบเวกเตอร์ที่มีเวกเตอร์เป็นศูนย์หรือเวกเตอร์ที่เท่ากันสองตัวจะขึ้นอยู่กับเชิงเส้นตรง

คุณสมบัติของเวกเตอร์ที่ขึ้นต่อเชิงเส้น

1. สำหรับเวกเตอร์ 2 และ 3 มิติ ตรงตามเงื่อนไขต่อไปนี้: เวกเตอร์ที่ขึ้นต่อเชิงเส้นสองตัวเป็นเส้นตรง เวกเตอร์คอลลิเนียร์สองตัวขึ้นอยู่กับเชิงเส้นตรง
2. สำหรับเวกเตอร์ 3 มิติ เป็นไปตามเงื่อนไขต่อไปนี้: เวกเตอร์ที่ขึ้นต่อเชิงเส้นสามตัวเป็นโคพลานาร์ (เวกเตอร์โคพลานาร์ 3 ตัวขึ้นอยู่กับเชิงเส้นตรง)
3. สำหรับเวกเตอร์ n มิติ เป็นไปตามเงื่อนไขต่อไปนี้: เวกเตอร์ n + 1 จะขึ้นอยู่กับเชิงเส้นเสมอ

ตัวอย่างการแก้ปัญหาเกี่ยวกับการพึ่งพาเชิงเส้นหรือความเป็นอิสระเชิงเส้นของเวกเตอร์

ตัวอย่างที่ 3

ลองตรวจสอบเวกเตอร์ a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 สำหรับความเป็นอิสระเชิงเส้น

สารละลาย. เวกเตอร์จะขึ้นอยู่กับเชิงเส้นตรงเนื่องจากขนาดของเวกเตอร์น้อยกว่าจำนวนเวกเตอร์

ตัวอย่างที่ 4

ลองตรวจสอบเวกเตอร์ a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1 เพื่อดูความเป็นอิสระเชิงเส้น

สารละลาย. เราค้นหาค่าสัมประสิทธิ์ที่ผลรวมเชิงเส้นจะเท่ากับเวกเตอร์ศูนย์:

x 1 ก + x 2 ข + x 3 ค 1 = 0

เราเขียนสมการเวกเตอร์ในรูปแบบเชิงเส้น:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

เราแก้ระบบนี้โดยใช้วิธีเกาส์:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

จากบรรทัดที่ 2 เราลบที่ 1 จากบรรทัดที่ 3 - 1:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

จากบรรทัดที่ 1 เราลบบรรทัดที่ 2 ไปจนถึงบรรทัดที่ 3 เราเพิ่มบรรทัดที่ 2:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

จากการแก้ปัญหาจึงตามมาว่าระบบมีวิธีแก้ปัญหามากมาย ซึ่งหมายความว่ามีการรวมกันที่ไม่ใช่ศูนย์ของค่าของตัวเลขดังกล่าว x 1, x 2, x 3 ซึ่งผลรวมเชิงเส้นของ a, b, c เท่ากับเวกเตอร์ศูนย์ ดังนั้น เวกเตอร์ a, b, c คือ ขึ้นอยู่กับเชิงเส้น

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดไฮไลต์แล้วกด Ctrl+Enter

เรียกว่าระบบเวกเตอร์ ขึ้นอยู่กับเชิงเส้นหากมีตัวเลขที่มีอย่างน้อยหนึ่งตัวแตกต่างจากศูนย์ เช่น ความเท่าเทียมกัน https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src= ">

หากความเท่าเทียมกันนี้เป็นที่พอใจเฉพาะในกรณีที่ เมื่อ ทั้งหมด ระบบของเวกเตอร์จะถูกเรียก เป็นอิสระเชิงเส้น.

ทฤษฎีบท.ระบบเวกเตอร์จะ ขึ้นอยู่กับเชิงเส้นถ้าหากเวกเตอร์อย่างน้อยหนึ่งตัวเป็นผลรวมเชิงเส้นของเวกเตอร์ตัวอื่น

ตัวอย่างที่ 1พหุนาม เป็นการรวมกันเชิงเส้นของพหุนาม https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24"> พหุนามประกอบขึ้นเป็นระบบอิสระเชิงเส้น เนื่องจาก พหุนาม https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">

ตัวอย่างที่ 2ระบบเมทริกซ์ , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> มีความเป็นอิสระเชิงเส้น เนื่องจากผลรวมเชิงเส้นเท่ากับ เมทริกซ์ศูนย์เฉพาะในกรณีที่ https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text /78/624 /images/image022_26.gif" width="40" height="21"> ขึ้นอยู่กับเชิงเส้น

สารละลาย.

มาสร้างผลรวมเชิงเส้นของเวกเตอร์เหล่านี้ https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" ความสูง = "22">.

พิกัดพิกัดที่มีชื่อเดียวกัน เวกเตอร์ที่เท่ากันเราได้รับ https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">

ในที่สุดเราก็ได้

และ

ระบบมีวิธีการแก้ปัญหาเล็กๆ น้อยๆ ที่ไม่เหมือนใคร ดังนั้นผลรวมเชิงเส้นของเวกเตอร์เหล่านี้จึงเท่ากับศูนย์เฉพาะในกรณีที่สัมประสิทธิ์ทั้งหมดเท่ากับศูนย์เท่านั้น ดังนั้น ระบบเวกเตอร์นี้จึงเป็นอิสระเชิงเส้น

ตัวอย่างที่ 4เวกเตอร์มีความเป็นอิสระเชิงเส้น ระบบเวกเตอร์จะเป็นอย่างไร?

ก);

ข)?

สารละลาย.

ก)ลองสร้างผลรวมเชิงเส้นแล้วจัดให้เป็นศูนย์

การใช้คุณสมบัติของการดำเนินการกับเวกเตอร์ในปริภูมิเชิงเส้นเราจะเขียนความเท่าเทียมกันสุดท้ายในรูปแบบใหม่

เนื่องจากเวกเตอร์มีความเป็นอิสระเชิงเส้น ค่าสัมประสิทธิ์ที่จะต้องเท่ากับศูนย์ เช่น..gif" width="12" height="23 src=">

ระบบสมการที่ได้จะมีคำตอบเล็กๆ น้อยๆ ที่ไม่เหมือนใคร .

ตั้งแต่ความเท่าเทียมกัน (*) ดำเนินการเฉพาะเมื่อhttps://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> – เป็นอิสระเชิงเส้น;

ข)มาสร้างความเท่าเทียมกันกันเถอะ https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)

เราได้รับการใช้เหตุผลที่คล้ายกัน

เราได้การแก้ระบบสมการโดยวิธีเกาส์

หรือ

ระบบหลังมี ชุดอนันต์วิธีแก้ปัญหา https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src="> ดังนั้นจึงมีชุดสัมประสิทธิ์ที่ไม่เป็นศูนย์ซึ่งมีความเท่าเทียมกัน ถือ (**) . ดังนั้นระบบเวกเตอร์ – ขึ้นอยู่กับเชิงเส้น

ตัวอย่างที่ 5ระบบของเวกเตอร์มีความเป็นอิสระเชิงเส้น และระบบของเวกเตอร์นั้นขึ้นอยู่กับเชิงเส้นตรง..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)

ในความเท่าเทียมกัน (***) . แท้จริงแล้ว ที่ ระบบจะขึ้นอยู่กับเชิงเส้นตรง

จากความสัมพันธ์ (***) เราได้รับ หรือ มาแสดงกันเถอะ .

เราได้รับ

งานสำหรับ การตัดสินใจที่เป็นอิสระ(ในกลุ่มผู้ชม)

1. ระบบที่มีเวกเตอร์เป็นศูนย์จะขึ้นอยู่กับเชิงเส้นตรง

2. ระบบประกอบด้วยเวกเตอร์หนึ่งตัว ก, จะขึ้นอยู่กับเชิงเส้นตรงก็ต่อเมื่อ ก=0.

3. ระบบที่ประกอบด้วยเวกเตอร์สองตัวจะขึ้นอยู่กับเวกเตอร์เชิงเส้นถ้าหากเวกเตอร์นั้นมีสัดส่วนกัน (นั่นคือ หนึ่งในนั้นได้มาจากอีกเวกเตอร์หนึ่งโดยการคูณด้วยตัวเลข)

4. หากคุณเพิ่มเวกเตอร์ให้กับระบบที่ขึ้นต่อเชิงเส้น คุณจะได้ระบบที่ขึ้นต่อเชิงเส้น

5. ถ้าเวกเตอร์ถูกลบออกจากระบบอิสระเชิงเส้น ดังนั้นผลลัพธ์ของระบบเวกเตอร์จะเป็นอิสระเชิงเส้น

6. ถ้าระบบ สเป็นอิสระเชิงเส้น แต่จะขึ้นต่อเชิงเส้นเมื่อเพิ่มเวกเตอร์ ขแล้วเวกเตอร์ ขแสดงเป็นเส้นตรงผ่านเวกเตอร์ของระบบ ส.

ค).ระบบเมทริกซ์ , , ในปริภูมิของเมทริกซ์ลำดับที่สอง

10. ปล่อยให้ระบบเวกเตอร์ ก,ขคสเปซเวกเตอร์มีความเป็นอิสระเชิงเส้น พิสูจน์ความเป็นอิสระเชิงเส้น ระบบต่อไปนี้เวกเตอร์:

ก)เอ+ข ข ค

ข)เอ+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">–หมายเลขใดก็ได้

ค).เอ+ข, ก+ค, ข+ค

11. อนุญาต ก,ขค– เวกเตอร์ 3 ตัวบนระนาบที่สามารถเกิดรูปสามเหลี่ยมได้ เวกเตอร์เหล่านี้จะขึ้นอยู่กับเชิงเส้นตรงหรือไม่?

12. ให้เวกเตอร์สองตัวมา a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). หาเวกเตอร์สี่มิติอีกสองตัว ก3 และก4เพื่อให้ระบบ เอ1,a2,a3,ก4มีความเป็นอิสระเชิงเส้นตรง .