เหตุใดแบบจำลองนักล่า-เหยื่อจึงไม่ถูกต้อง การสั่นของระบบล่าเหยื่อ (แบบจำลอง Lotka-Voltaire)

ผู้ล่าสามารถกินสัตว์กินพืชและสัตว์นักล่าที่อ่อนแอได้ ผู้ล่ามีอาหารหลากหลายและสลับจากเหยื่อตัวหนึ่งไปยังอีกตัวหนึ่งได้อย่างง่ายดายและเข้าถึงได้ง่ายกว่า ผู้ล่ามักโจมตีเหยื่อที่อ่อนแอ รักษาสมดุลทางนิเวศวิทยาระหว่างประชากรที่เป็นเหยื่อและนักล่า[...]

หากสมดุลไม่เสถียร (ไม่มีรอบจำกัด) หรือวงจรภายนอกไม่เสถียร จำนวนสัตว์ทั้งสองชนิดที่ประสบความผันผวนอย่างรุนแรงจะออกจากบริเวณสมดุล ยิ่งไปกว่านั้น การเสื่อมสภาพอย่างรวดเร็ว (ในสถานการณ์แรก) เกิดขึ้นเมื่อมีการปรับตัวของนักล่าต่ำ เช่น มีอัตราการเสียชีวิตสูง (เทียบกับอัตราการแพร่พันธุ์ของเหยื่อ) ซึ่งหมายความว่านักล่าที่อ่อนแอทุกประการไม่ได้มีส่วนช่วยในการรักษาเสถียรภาพของระบบและตัวมันเองก็ตายไป[...]

ความกดดันของผู้ล่าจะรุนแรงเป็นพิเศษเมื่อในการวิวัฒนาการร่วมกันของผู้ล่าและเหยื่อ ความสมดุลจะเปลี่ยนไปทางผู้ล่าและระยะของเหยื่อแคบลง การต่อสู้ทางการแข่งขันมีความสัมพันธ์อย่างใกล้ชิดกับการขาดแคลนทรัพยากรอาหาร นอกจากนี้ยังอาจเป็นการต่อสู้โดยตรง เช่น การล่าพื้นที่เป็นทรัพยากร แต่ส่วนใหญ่มักเป็นเพียงการแทนที่ของสายพันธุ์ที่ไม่มีอาหารเพียงพอใน กำหนดอาณาเขตโดยสายพันธุ์ที่มีอาหารในปริมาณเท่ากัน นี่เป็นการแข่งขันระหว่างทางแล้ว[...]

และสุดท้าย ในระบบ "นักล่า - เหยื่อ" ที่อธิบายโดยแบบจำลอง (2.7) การเกิดขึ้นของความไม่แน่นอนของการแพร่กระจาย (ด้วยความเสถียรของความสมดุลในท้องถิ่น) จะเกิดขึ้นได้เฉพาะในกรณีที่การตายตามธรรมชาติของนักล่าเพิ่มขึ้นตามการเติบโตของจำนวนประชากรเร็วกว่า ฟังก์ชันเชิงเส้นและฟังก์ชันทางโภชนาการแตกต่างจากโวลแตร์ราหรือเมื่อประชากรเหยื่อเป็นประชากรประเภทโอลลี่[...]

ตามทฤษฎีแล้ว ในแบบจำลอง "นักล่าหนึ่งตัว - เหยื่อสองตัว" การแทะเล็มหญ้าที่เท่าเทียมกัน (ขาดความชอบสำหรับสายพันธุ์เหยื่อหนึ่งหรือสายพันธุ์อื่น) อาจส่งผลกระทบต่อการอยู่ร่วมกันในการแข่งขันของสายพันธุ์เหยื่อเฉพาะในสถานที่เหล่านั้นซึ่งมีความสมดุลที่เสถียรอยู่แล้ว ความหลากหลายสามารถเพิ่มขึ้นได้เฉพาะภายใต้เงื่อนไขที่สายพันธุ์ที่มีความสามารถในการแข่งขันน้อยกว่ามีอัตราการเติบโตของประชากรที่สูงกว่าสายพันธุ์ที่โดดเด่น สิ่งนี้ช่วยให้เราเข้าใจสถานการณ์เมื่อการแทะเล็มสม่ำเสมอนำไปสู่การเพิ่มความหลากหลายของพันธุ์พืชโดยที่สายพันธุ์จำนวนมากที่ได้รับการคัดเลือกเพื่อการสืบพันธุ์อย่างรวดเร็วอยู่ร่วมกับสายพันธุ์ที่วิวัฒนาการมุ่งเป้าไปที่การเพิ่มขีดความสามารถในการแข่งขัน [...]

ในทำนองเดียวกัน การเลือกเหยื่อที่ขึ้นกับความหนาแน่นสามารถนำไปสู่ความสมดุลที่มั่นคงในแบบจำลองทางทฤษฎีของเหยื่อสองสายพันธุ์ที่แข่งขันกันซึ่งไม่มีความสมดุลมาก่อน เมื่อต้องการทำเช่นนี้ ผู้ล่าจะต้องมีความสามารถในการตอบสนองเชิงตัวเลขและเชิงฟังก์ชันต่อการเปลี่ยนแปลงความหนาแน่นของเหยื่อ อย่างไรก็ตาม เป็นไปได้ว่าการสับเปลี่ยน (การโจมตีเหยื่อที่มีจำนวนมากที่สุดบ่อยครั้งอย่างไม่เป็นสัดส่วน) จะมีความสำคัญมากกว่า ในความเป็นจริง มีการพิสูจน์แล้วว่าการสลับมีผลในการรักษาเสถียรภาพในระบบ "ผู้ล่าหนึ่งคน - เหยื่อ" และแสดงถึงกลไกเดียวที่สามารถรักษาเสถียรภาพของการโต้ตอบในกรณีที่ช่องเหยื่อทับซ้อนกันโดยสิ้นเชิง ผู้ล่าที่ไม่เชี่ยวชาญสามารถมีบทบาทเช่นนี้ได้ การเลือกโดยผู้ล่าที่เชี่ยวชาญมากกว่าสำหรับคู่แข่งที่โดดเด่นจะทำในลักษณะเดียวกับการสลับนักล่า และสามารถทำให้ปฏิสัมพันธ์ทางทฤษฎีมีความเสถียรในแบบจำลองซึ่งก่อนหน้านี้ไม่มีความสมดุลระหว่างสายพันธุ์เหยื่อ โดยมีเงื่อนไขว่าช่องของพวกมันจะต้องแยกจากกันในระดับหนึ่ง[...]

นอกจากนี้นักล่าที่ "แข็งแกร่งทุกประการ" ไม่ได้ทำให้ชุมชนมั่นคงเช่น ปรับตัวเข้ากับเหยื่อได้ดีและมีอัตราการตายต่ำ ในกรณีนี้ ระบบมีวงจรจำกัดที่ไม่เสถียร และแม้จะมีความเสถียรของตำแหน่งสมดุล แต่ก็เสื่อมถอยลงในสภาพแวดล้อมแบบสุ่ม (นักล่ากินเหยื่อและผลที่ตามมาก็ตาย) สถานการณ์นี้สอดคล้องกับการเสื่อมสภาพช้า[...]

ดังนั้นด้วยการปรับตัวที่ดีของนักล่าในบริเวณใกล้เคียงกับสมดุลที่มั่นคง วงจรที่ไม่เสถียรและเสถียรก็สามารถเกิดขึ้นได้ เช่น ขึ้นอยู่กับเงื่อนไขเริ่มต้นระบบ "นักล่า - เหยื่อ" มีแนวโน้มที่จะสมดุลหรือสั่นเคลื่อนตัวออกจากมันหรือความผันผวนที่มั่นคงในจำนวนของทั้งสองสายพันธุ์นั้นถูกสร้างขึ้นในบริเวณใกล้เคียงของความสมดุล [... ]

สิ่งมีชีวิตที่จัดอยู่ในประเภทผู้ล่ากินสิ่งมีชีวิตอื่นและทำลายเหยื่อของพวกมัน ดังนั้น ในบรรดาสิ่งมีชีวิต ควรแยกแยะระบบการจำแนกประเภทเพิ่มเติมอีกระบบหนึ่ง ได้แก่ "ผู้ล่า" และ "เหยื่อ" ความสัมพันธ์ระหว่างสิ่งมีชีวิตดังกล่าวได้พัฒนาตลอดวิวัฒนาการของสิ่งมีชีวิตบนโลกของเรา สิ่งมีชีวิตที่กินสัตว์อื่นทำหน้าที่เป็นตัวควบคุมตามธรรมชาติของจำนวนสิ่งมีชีวิตที่เป็นเหยื่อ การเพิ่มจำนวน "ผู้ล่า" จะทำให้จำนวน "เหยื่อ" ลดลง ในทางกลับกัน จะช่วยลดการจัดหาอาหาร ("เหยื่อ") สำหรับ "ผู้ล่า" ซึ่งโดยทั่วไปจะกำหนดจำนวนที่ลดลง ของ "เหยื่อ" ฯลฯ ดังนั้นใน biocenosis ความผันผวนของจำนวนผู้ล่าและเหยื่อเกิดขึ้นอย่างต่อเนื่อง แต่โดยทั่วไปแล้วความสมดุลบางอย่างจะเกิดขึ้นในช่วงระยะเวลาหนึ่งภายใต้สภาพแวดล้อมที่ค่อนข้างคงที่[... ]

ในที่สุดสิ่งนี้ก็มาถึงความสมดุลทางนิเวศวิทยาระหว่างประชากรนักล่าและเหยื่อ[...]

สำหรับฟังก์ชันทางโภชนาการประเภทที่สาม สถานะสมดุลจะคงที่หากโดยที่ N คือจุดเปลี่ยนเว้าของฟังก์ชัน (ดูรูปที่ 2, c) สิ่งนี้ตามมาจากข้อเท็จจริงที่ว่าเมื่อเวลาผ่านไป ฟังก์ชั่นทางโภชนาการจะเว้า ดังนั้นส่วนแบ่งสัมพัทธ์ของการบริโภคเหยื่อโดยนักล่าจึงเพิ่มขึ้น[...]

ให้ Гг = -Г คือ มีชุมชนประเภท "ล่าเหยื่อ" ในกรณีนี้ เทอมแรกในนิพจน์ (7.4) มีค่าเท่ากับศูนย์ และเพื่อให้เป็นไปตามเงื่อนไขความเสถียรในแง่ของความน่าจะเป็นของสถานะสมดุล N เทอมที่สองจะต้องไม่เป็นค่าบวกเช่นกัน[.. .]

ดังนั้น สำหรับชุมชนผู้ล่าและเหยื่อที่ถูกพิจารณา เราสามารถสรุปได้ว่าตำแหน่งสมดุลเชิงบวกโดยรวมนั้นมีความเสถียรเชิงแสดงสัญญาณ กล่าวคือ สำหรับข้อมูลเริ่มต้นใดๆ 1H(0)>0 วิวัฒนาการจะเกิดขึ้นในลักษณะที่ N(7) - ■ K โดยมีเงื่อนไขว่า N >0.[...]

ดังนั้นในสภาพแวดล้อมที่เป็นเนื้อเดียวกันซึ่งไม่มีที่พักพิงสำหรับการสืบพันธุ์นักล่าไม่ช้าก็เร็วจะทำลายประชากรของเหยื่อแล้วตายไปเอง คลื่นแห่งชีวิต” (การเปลี่ยนแปลงในความอุดมสมบูรณ์ของผู้ล่าและเหยื่อ) ติดตามซึ่งกันและกันด้วยการเปลี่ยนเฟสอย่างต่อเนื่อง และโดยเฉลี่ยแล้ว ความอุดมสมบูรณ์ของทั้งผู้ล่าและเหยื่อยังคงอยู่ที่ระดับเดียวกันโดยประมาณ ระยะเวลาขึ้นอยู่กับอัตราการเจริญเติบโตของทั้งสองชนิดและค่าพารามิเตอร์เริ่มต้น สำหรับประชากรที่เป็นเหยื่อ อิทธิพลของนักล่านั้นเป็นไปในทางบวก เนื่องจากการสืบพันธุ์ที่มากเกินไปจะนำไปสู่การล่มสลายของประชากร ในทางกลับกัน กลไกทั้งหมดที่ขัดขวางการทำลายล้างเหยื่อโดยสมบูรณ์มีส่วนช่วยในการรักษาแหล่งอาหารของนักล่า[...]

การปรับเปลี่ยนอื่นๆ อาจเป็นผลมาจากพฤติกรรมของผู้ล่า จำนวนเหยื่อที่ผู้ล่าสามารถกินเข้าไปได้ เวลาที่กำหนด, มีขีดจำกัดของมัน ผลกระทบของความอิ่มตัวของนักล่าเมื่อเข้าใกล้เกณฑ์นี้แสดงไว้ในตารางที่ 1 2-4, B. ปฏิกิริยาที่อธิบายไว้ในสมการที่ 5 และ 6 อาจมีจุดสมดุลที่เสถียรหรือแสดงความผันผวนแบบวัฏจักร อย่างไรก็ตาม วัฏจักรดังกล่าวแตกต่างจากที่แสดงในสมการ Lotka-Volterra 1 และ 2 วัฏจักรที่ถ่ายทอดโดยสมการที่ 5 และ 6 สามารถมีแอมพลิจูดคงที่และความหนาแน่นเฉลี่ยตราบใดที่ตัวกลางคงที่ หลังจากเกิดการรบกวน พวกเขาสามารถกลับสู่แอมพลิจูดและความหนาแน่นเฉลี่ยก่อนหน้าได้ วงจรดังกล่าวที่ฟื้นตัวจากการรบกวนเรียกว่าวงจรจำกัดที่เสถียร ปฏิสัมพันธ์ระหว่างกระต่ายกับแมวป่าชนิดหนึ่งถือได้ว่าเป็นวงจรจำกัดที่มั่นคง แต่ไม่ใช่วงจร Lotka-Volterra[...]

ให้เราพิจารณาการเกิดความไม่เสถียรของการแพร่กระจายในระบบนักล่า-เหยื่อ แต่ก่อนอื่น เราจะเขียนเงื่อนไขที่รับประกันการเกิดความไม่เสถียรของการแพร่กระจายในระบบ (1.1) โดยมี n = 2 เป็นที่ชัดเจนว่าสมดุล (N, N ) เป็นภาษาท้องถิ่น (เช่น[ .. .]

ให้เรามาดูการตีความกรณีที่เกี่ยวข้องกับการอยู่ร่วมกันของผู้ล่าและเหยื่อในระยะยาว เป็นที่ชัดเจนว่าหากไม่มีวงจรจำกัด สมดุลที่เสถียรจะสอดคล้องกับความผันผวนของประชากรในสภาพแวดล้อมแบบสุ่ม และแอมพลิจูดของวงจรดังกล่าวจะเป็นสัดส่วนกับการกระจายตัวของการรบกวน ปรากฏการณ์นี้จะเกิดขึ้นหากผู้ล่ามีอัตราการตายสัมพัทธ์สูงและในขณะเดียวกันก็มีความสามารถในการปรับตัวกับเหยื่อในระดับสูง[...]

ให้เราพิจารณาว่าไดนามิกของระบบเปลี่ยนแปลงไปอย่างไรเมื่อสมรรถภาพของนักล่าเพิ่มขึ้นเช่น โดยที่ b ลดลงจาก 1 เป็น 0 หากสมรรถภาพร่างกายต่ำเพียงพอ ก็จะไม่มีรอบขีดจำกัด และความสมดุลจะไม่เสถียร ด้วยสมรรถภาพที่เพิ่มขึ้นในบริเวณใกล้เคียงของสมดุลนี้ วงจรที่มั่นคงและจากนั้นวงจรภายนอกที่ไม่เสถียรอาจปรากฏขึ้น ขึ้นอยู่กับเงื่อนไขเริ่มต้น (อัตราส่วนของชีวมวลของผู้ล่าและเหยื่อ) ระบบอาจสูญเสียความเสถียร เช่น ออกจากบริเวณใกล้เคียงของความสมดุล มิฉะนั้นการแกว่งที่เสถียรจะถูกสร้างขึ้นเมื่อเวลาผ่านไป การเติบโตของสมรรถภาพทำให้ลักษณะการสั่นไหวของพฤติกรรมของระบบเป็นไปไม่ได้ อย่างไรก็ตาม เมื่อข [...]

ตัวอย่างของผลตอบรับเชิงลบ (ทำให้เสถียร) คือความสัมพันธ์ระหว่างผู้ล่ากับเหยื่อ หรือการทำงานของระบบคาร์บอเนตในมหาสมุทร (สารละลาย CO2 ในน้ำ: CO2 + H2O -> H2CO3) โดยปกติแล้ว ปริมาณคาร์บอนไดออกไซด์ที่ละลายในน้ำทะเลจะอยู่ในสมดุลบางส่วนกับความเข้มข้น คาร์บอนไดออกไซด์ในบรรยากาศ การเพิ่มขึ้นของก๊าซคาร์บอนไดออกไซด์ในท้องถิ่นในชั้นบรรยากาศหลังจากการปะทุของภูเขาไฟนำไปสู่การสังเคราะห์ด้วยแสงที่เข้มข้นขึ้นและการดูดซับโดยระบบคาร์บอเนตในมหาสมุทร เมื่อระดับคาร์บอนไดออกไซด์ในบรรยากาศลดลง ระบบคาร์บอเนตในมหาสมุทรจะปล่อยก๊าซคาร์บอนไดออกไซด์ออกสู่ชั้นบรรยากาศ ดังนั้นความเข้มข้นของก๊าซคาร์บอนไดออกไซด์ในชั้นบรรยากาศจึงค่อนข้างคงที่[...]

[ ...]

ตามที่ระบุไว้โดย R. Ricklefs (1979) มีปัจจัยหลายประการที่ส่งผลต่อการรักษาเสถียรภาพของความสัมพันธ์ในระบบ "นักล่า-เหยื่อ": ความไร้ประสิทธิภาพของผู้ล่า ความพร้อมของแหล่งอาหารทางเลือกสำหรับผู้ล่า การลดความล่าช้าในการ ปฏิกิริยาของนักล่า เช่นเดียวกับข้อจำกัดด้านสิ่งแวดล้อมที่กำหนด สภาพแวดล้อมภายนอกสำหรับประชากรกลุ่มหนึ่งหรือกลุ่มอื่น ปฏิสัมพันธ์ระหว่างประชากรนักล่าและเหยื่อมีความหลากหลายและซับซ้อนมาก ดังนั้น หากผู้ล่ามีประสิทธิภาพเพียงพอ พวกมันก็จะสามารถควบคุมความหนาแน่นของประชากรของเหยื่อได้ โดยรักษาให้ต่ำกว่าความสามารถในการรองรับของสิ่งแวดล้อม ด้วยอิทธิพลที่พวกมันมีต่อประชากรเหยื่อ ผู้ล่ามีอิทธิพลต่อวิวัฒนาการของลักษณะต่างๆ ของเหยื่อ ซึ่งท้ายที่สุดจะนำไปสู่ความสมดุลทางนิเวศวิทยาระหว่างประชากรของผู้ล่าและเหยื่อ[...]

หากตรงตามเงื่อนไขข้อใดข้อหนึ่ง: 0 1/2 ถ้า 6 > 1 (kA [...]

ความเสถียรของสิ่งมีชีวิตและสิ่งแวดล้อมขึ้นอยู่กับปฏิสัมพันธ์ของพืชเท่านั้น - ออโตโทรฟและสิ่งมีชีวิตเฮเทอโรโทรฟิคที่กินพืชเป็นอาหาร ผู้ล่าทุกขนาดไม่สามารถรบกวนความสมดุลทางนิเวศน์ของชุมชนได้ตั้งแต่นั้นเป็นต้นมา สภาพธรรมชาติพวกเขาไม่สามารถเพิ่มจำนวนเหยื่อให้มีจำนวนคงที่ได้ ผู้ล่าไม่เพียงแต่จะต้องเคลื่อนที่ได้เองเท่านั้น แต่ยังสามารถกินเฉพาะสัตว์ที่เคลื่อนไหวได้อีกด้วย[...]

ไม่มีปลาชนิดอื่นใดที่แพร่หลายเท่าหอก ในพื้นที่ตกปลาบางแห่งในอ่างเก็บน้ำแบบยืนหรือไหล ไม่มีแรงกดดันจากหอกเพื่อรักษาสมดุลระหว่างเหยื่อและผู้ล่า มีเพียงอ่างเก็บน้ำเทียมสมัยใหม่เท่านั้นที่หอกเป็นปลาที่ไม่พึงประสงค์เนื่องจากการเพาะพันธุ์ของปลาชนิดอื่นในบริเวณนั้นเท่านั้นที่ไม่ได้รับการประชากรโดยเจตนา พวกเขา. ไพค์เป็นตัวแทนได้ดีที่สุดในโลก พวกมันถูกจับได้ทั่วซีกโลกเหนือตั้งแต่สหรัฐอเมริกาและแคนาดาไปจนถึง อเมริกาเหนือผ่านทางยุโรปไปจนถึงเอเชียเหนือ[...]

ความเป็นไปได้อีกอย่างหนึ่งของการอยู่ร่วมกันอย่างยั่งยืนเกิดขึ้นที่นี่ ในช่วงการปรับตัวที่ค่อนข้างแคบ เมื่อเปลี่ยนไปสู่ระบอบการปกครองที่ไม่เสถียรกับนักล่าที่ "ดี" มาก วงจรขีดจำกัดภายนอกที่เสถียรอาจเกิดขึ้น ซึ่งการกระจายของชีวมวลจะมีความสมดุลโดยการไหลเข้าสู่ระบบ (ผลผลิตสูงของเหยื่อ) จากนั้นสถานการณ์ที่น่าสงสัยก็เกิดขึ้นเมื่อค่าลักษณะเฉพาะสองค่าของแอมพลิจูดของการแกว่งแบบสุ่มเป็นไปได้มากที่สุด บางอย่างเกิดขึ้นใกล้สมดุล บางอย่าง - ใกล้วงจรจำกัด และอาจมีการเปลี่ยนผ่านระหว่างระบอบการปกครองเหล่านี้บ่อยครั้งไม่มากก็น้อย [...]

ประชากรสมมุติที่ทำงานตามเวกเตอร์ในรูปที่ 10.11 A แสดงไว้ในรูปที่ 1 10.11,-B ใช้กราฟที่แสดงพลวัตของอัตราส่วนของประชากรผู้ล่าและเหยื่อ และในรูปที่ 10.11,-B 10.11.5 ในรูปแบบของกราฟพลวัตของจำนวนผู้ล่าและเหยื่อเมื่อเวลาผ่านไป ในประชากรที่เป็นเหยื่อ เมื่อมันเคลื่อนจากสมดุลความหนาแน่นต่ำไปสู่สมดุลความหนาแน่นสูง แล้วกลับมา ตัวเลข "ระเบิด" จะเกิดขึ้น และตัวเลขที่เพิ่มขึ้นนี้ไม่ได้เป็นผลมาจากการเปลี่ยนแปลงที่เด่นชัดเท่าเทียมกัน สิ่งแวดล้อม. ในทางตรงกันข้าม การเปลี่ยนแปลงของตัวเลขนี้เกิดจากการกระแทก (โดยมี "เสียงรบกวน" ในสภาพแวดล้อมเล็กน้อย) และโดยเฉพาะอย่างยิ่ง มันสะท้อนให้เห็นถึงการดำรงอยู่ของสภาวะสมดุลหลายแห่ง การใช้เหตุผลที่คล้ายกันนี้สามารถใช้เพื่ออธิบายกรณีที่ซับซ้อนมากขึ้นของพลวัตของประชากรในประชากรธรรมชาติ[...]

ทรัพย์สินที่สำคัญที่สุดระบบนิเวศคือความมั่นคง ความสมดุลของการแลกเปลี่ยน และกระบวนการที่เกิดขึ้นในนั้น ความสามารถของประชากรหรือระบบนิเวศในการรักษาสมดุลไดนามิกที่มั่นคงในการเปลี่ยนแปลงสภาพแวดล้อมเรียกว่าสภาวะสมดุล (homoios - เหมือนกัน, คล้ายกัน, ภาวะหยุดนิ่ง - สถานะ) สภาวะสมดุลจะขึ้นอยู่กับหลักการป้อนกลับ เพื่อรักษาความสมดุลในธรรมชาติ จึงไม่จำเป็นต้องมีการควบคุมจากภายนอก ตัวอย่างของสภาวะสมดุลคือระบบย่อย "นักล่า-เหยื่อ" ซึ่งควบคุมความหนาแน่นของประชากรของผู้ล่าและเหยื่อ[...]

ระบบนิเวศทางธรรมชาติ(biogeocenosis) ทำงานได้อย่างเสถียรโดยมีปฏิสัมพันธ์อย่างต่อเนื่องขององค์ประกอบ การไหลเวียนของสาร การถ่ายโอนสารเคมี พลังงาน พันธุกรรมและพลังงานและข้อมูลอื่น ๆ ผ่านช่องทางโซ่ ตามหลักการของความสมดุล ระบบธรรมชาติใดๆ ที่มีพลังงานและข้อมูลไหลผ่านมีแนวโน้มที่จะพัฒนาสภาวะคงตัว ขณะเดียวกัน เสถียรภาพของระบบนิเวศก็มั่นใจได้โดยอัตโนมัติผ่านกลไกตอบรับ ผลตอบรับประกอบด้วยการใช้ข้อมูลที่ได้รับจากองค์ประกอบที่ได้รับการจัดการของระบบนิเวศเพื่อทำการปรับเปลี่ยนกระบวนการโดยองค์ประกอบการจัดการ ความสัมพันธ์ระหว่าง "นักล่า" กับ "เหยื่อ" ที่กล่าวถึงข้างต้นในบริบทนี้สามารถอธิบายได้อย่างละเอียดมากขึ้น ใช่แล้ว ในระบบนิเวศทางน้ำ ปลานักล่า(หอกในบ่อ) กินปลาเหยื่อชนิดอื่น (ปลาคาร์พ crucian); หากจำนวนปลาคาร์พ crucian เพิ่มขึ้นนี่คือตัวอย่างของการตอบรับเชิงบวก หอกกินปลาคาร์พ crucian ลดจำนวนลง - นี่คือตัวอย่างของการตอบรับเชิงลบ เมื่อจำนวนผู้ล่าเพิ่มขึ้น จำนวนเหยื่อก็ลดลง และผู้ล่าที่ประสบภาวะขาดอาหารก็จะลดการเติบโตของประชากรด้วย ในท้ายที่สุด ในบ่อที่มีปัญหา ความสมดุลแบบไดนามิกถูกสร้างขึ้นในจำนวนปลาหอกและปลาคาร์พ crucian รักษาสมดุลอย่างต่อเนื่องซึ่งจะไม่รวมการหายไปของการเชื่อมโยงใด ๆ ในห่วงโซ่อาหาร (รูปที่ 64)[...]

เรามาดูภาพรวมที่สำคัญที่สุดกันดีกว่า กล่าวคือ ปฏิสัมพันธ์เชิงลบจะสังเกตเห็นได้น้อยลงเมื่อเวลาผ่านไป หากระบบนิเวศมีเสถียรภาพเพียงพอ และโครงสร้างเชิงพื้นที่ช่วยให้ประชากรปรับตัวร่วมกันได้ ในระบบโมเดลเช่น นักล่าเหยื่ออธิบายโดยสมการ Lotka-Volterra หากไม่มีการนำคำศัพท์เพิ่มเติมเข้ามาในสมการ ซึ่งแสดงลักษณะของปัจจัยที่จำกัดตัวเองของตัวเลข การแกว่งจะเกิดขึ้นอย่างต่อเนื่องและไม่ตายไป (ดู Lewontin, 1969) Pimentel (1968; ดู Pimentel และ Stone, 1968 ด้วย) แสดงให้เห็นการทดลองว่าคำศัพท์เพิ่มเติมดังกล่าวอาจสะท้อนถึงการปรับตัวหรือทางพันธุกรรมร่วมกัน ข้อเสนอแนะ. เมื่อมีการสร้างวัฒนธรรมใหม่จากบุคคลที่อยู่ร่วมกันก่อนหน้านี้เป็นเวลาสองปีในวัฒนธรรมที่จำนวนของพวกเขาขึ้นอยู่กับความผันผวนอย่างมาก ปรากฎว่าพวกเขาพัฒนาสภาวะสมดุลทางนิเวศน์ ซึ่งประชากรแต่ละกลุ่มถูก "ปราบปราม" โดยอีกฝ่ายหนึ่ง ระดับที่ปรากฎว่าสามารถอยู่ร่วมกันได้อย่างสมดุลมากขึ้น

การสร้างแบบจำลองทางคณิตศาสตร์ของกระบวนการทางชีววิทยาเริ่มต้นด้วยการสร้างแบบจำลองง่ายๆ ตัวแรกของระบบนิเวศ

สมมติว่าแมวป่าชนิดหนึ่งและกระต่ายอาศัยอยู่ในพื้นที่ปิดบางแห่ง Lynxes กินเฉพาะกระต่ายและกระต่าย - อาหารจากพืชมีจำหน่ายใน ปริมาณไม่จำกัด. มีความจำเป็นต้องค้นหาลักษณะมหภาคที่อธิบายประชากร ลักษณะเหล่านี้คือจำนวนบุคคลในประชากร

รูปแบบที่ง่ายที่สุดความสัมพันธ์ระหว่างประชากรนักล่าและเหยื่อ ตามสมการการเติบโตลอจิสติกส์ ได้รับการตั้งชื่อ (เช่นแบบจำลองของการแข่งขันแบบเฉพาะเจาะจง) ตามผู้สร้าง - Lotka และ Volterra แบบจำลองนี้ช่วยลดความซับซ้อนของสถานการณ์ที่กำลังศึกษาอยู่อย่างมาก แต่ก็ยังมีประโยชน์เป็นจุดเริ่มต้นในการวิเคราะห์ระบบนักล่าและเหยื่อ

ให้เราสมมติว่า (1) ประชากรเหยื่อมีอยู่ในสภาพแวดล้อมในอุดมคติ (ไม่ขึ้นกับความหนาแน่น) ซึ่งการเติบโตของมันถูกจำกัดโดยการปรากฏตัวของผู้ล่าเท่านั้น (2) มีสภาพแวดล้อมในอุดมคติที่เท่าเทียมกันซึ่งมีผู้ล่าที่มีประชากร การเจริญเติบโตถูกจำกัดด้วยความอุดมสมบูรณ์ของเหยื่อเท่านั้น (3 ) ประชากรทั้งสองแพร่พันธุ์อย่างต่อเนื่องตามสมการการเติบโตแบบเอ็กซ์โปเนนเชียล (4) อัตราการบริโภคเหยื่อโดยผู้ล่าเป็นสัดส่วนกับความถี่ของการพบกันระหว่างพวกมัน ซึ่งในทางกลับกัน เป็นฟังก์ชันของความหนาแน่นของประชากร สมมติฐานเหล่านี้รองรับแบบจำลอง Lotka-Volterra

ปล่อยให้ประชากรเหยื่อเติบโตแบบทวีคูณในกรณีที่ไม่มีผู้ล่า:

dN/dt =r 1 N 1

โดยที่ N คือตัวเลข และ r คืออัตราการเติบโตทันทีทันใดของประชากรเหยื่อ หากมีผู้ล่าอยู่ พวกมันจะทำลายเหยื่อในอัตราที่กำหนด ประการแรก ตามความถี่ของการพบปะกันระหว่างผู้ล่ากับเหยื่อ ซึ่งจะเพิ่มขึ้นตามจำนวนที่เพิ่มขึ้น และประการที่สอง ตามประสิทธิภาพที่ผู้ล่าตรวจจับและจับได้ ตกเป็นเหยื่อเมื่อพบกัน จำนวนเหยื่อที่นักล่าหนึ่งคนพบและกิน N c นั้นแปรผันตามประสิทธิภาพการล่าสัตว์ซึ่งเราแสดงผ่านสัมประสิทธิ์ C 1 จำนวน (ความหนาแน่น) ของเหยื่อ N และเวลาที่ใช้ในการค้นหา ที:

ยังไม่มีข้อความ C = C 1 NT(1)

จากสำนวนนี้ มันง่ายที่จะกำหนดอัตราเฉพาะของการบริโภคเหยื่อโดยผู้ล่า (เช่น จำนวนเหยื่อที่ผู้ล่าหนึ่งคนกินต่อหน่วยเวลา) ซึ่งมักเรียกอีกอย่างว่าการตอบสนองเชิงการทำงานของผู้ล่าต่อความหนาแน่นของประชากร ของเหยื่อ:

ในรุ่นที่กำลังพิจารณา ค 1เป็นค่าคงที่ ซึ่งหมายความว่าจำนวนเหยื่อที่ถูกกำจัดออกจากประชากรโดยผู้ล่าจะเพิ่มขึ้นเป็นเส้นตรงกับความหนาแน่นของประชากรที่เพิ่มขึ้น (ที่เรียกว่าการตอบสนองเชิงหน้าที่ประเภท 1) มันชัดเจนว่า ความเร็วโดยรวมการบริโภคเหยื่อของนักล่าทุกคนจะเป็น:

(3)

ที่ไหน ร -ขนาดประชากรนักล่า ตอนนี้เราสามารถเขียนสมการการเติบโตของประชากรเหยื่อได้ดังนี้:

ในกรณีที่ไม่มีเหยื่อ ผู้ล่าจะอดอาหารและตาย ให้เราสมมติด้วยว่าในกรณีนี้ประชากรนักล่าจะลดลงแบบทวีคูณตามสมการ:

(5)

ที่ไหน ร 2- การตายทันทีทันใดในประชากรนักล่า

หากมีเหยื่อ ผู้ล่าที่สามารถค้นหาและกินพวกมันได้ก็จะสืบพันธุ์ อัตราการเกิดของประชากรผู้ล่าในแบบจำลองนี้ขึ้นอยู่กับสองสถานการณ์เท่านั้น ได้แก่ อัตราการบริโภคเหยื่อโดยผู้ล่า และประสิทธิภาพที่ผู้ล่าแปรรูปอาหารที่บริโภคไปเป็นลูกหลานของมัน หากเราแสดงประสิทธิภาพนี้ผ่านสัมประสิทธิ์ s อัตราการเกิดจะเป็น:

เนื่องจาก C 1 และ s เป็นค่าคงที่ ผลคูณของพวกมันจึงเป็นค่าคงที่เช่นกัน ซึ่งเราแสดงว่าเป็น C 2 จากนั้นอัตราการเติบโตของประชากรผู้ล่าจะถูกกำหนดโดยความสมดุลของภาวะเจริญพันธุ์และอัตราการตายตามสมการ:

(6)

สมการที่ 4 และ 6 รวมกันเป็นแบบจำลอง Lotka-Volterra

เราสามารถศึกษาคุณสมบัติของแบบจำลองนี้ได้ในลักษณะเดียวกับในกรณีของการแข่งขันนั่นคือ โดยการสร้างแผนภาพเฟสโดยพล็อตจำนวนเหยื่อตามแกนกำหนด และผู้ล่าถูกพล็อตไปตามแกนแอบซิสซา และวาดเส้นไอโซไลน์บนมันที่สอดคล้องกับขนาดประชากรคงที่ ด้วยความช่วยเหลือของ isoclines พฤติกรรมของการโต้ตอบระหว่างประชากรของนักล่าและเหยื่อจะถูกกำหนด

สำหรับประชากรที่เป็นเหยื่อ: ที่ไหน

ดังนั้น เนื่องจาก r และ C 1 เป็นค่าคงที่ ไอโซไลน์ของเหยื่อจะเป็นเส้นที่จำนวนผู้ล่า (ร)คงที่ กล่าวคือ ขนานกับแกน x แล้วตัดแกนพิกัดที่จุดนั้น ป =ร 1 /ค 1. เหนือเส้นนี้จำนวนเหยื่อจะลดลง และต่ำกว่านั้นก็จะเพิ่มขึ้น

สำหรับประชากรนักล่า:

ที่ไหน

เพราะว่า ร 2และ C 2 - ค่าคงที่ isocline สำหรับนักล่าจะเป็นเส้นที่จำนวนเหยื่อ (N) คงที่เช่น ตั้งฉากกับแกนพิกัดและตัดแกน abscissa ที่จุด N = r 2 /C 2 . ทางด้านซ้ายจำนวนผู้ล่าจะลดลง และทางขวาก็จะเพิ่มขึ้น

หากเราพิจารณาไอโซไลน์ทั้งสองนี้รวมกัน เราจะสังเกตเห็นได้ง่ายว่าปฏิสัมพันธ์ระหว่างประชากรของผู้ล่าและเหยื่อนั้นเป็นวัฏจักร เนื่องจากจำนวนของพวกมันมีความผันผวนแบบคอนจูเกตไม่จำกัด เมื่อจำนวนเหยื่อสูง จำนวนผู้ล่าก็จะเพิ่มขึ้น ซึ่งนำไปสู่ความกดดันในการล่าเหยื่อเพิ่มขึ้นและทำให้จำนวนเหยื่อลดลง การลดลงนี้นำไปสู่การขาดอาหารสำหรับผู้ล่าและจำนวนที่ลดลงซึ่งทำให้ความกดดันในการปล้นสะดมลดลงและจำนวนเหยื่อที่เพิ่มขึ้นซึ่งนำไปสู่การเพิ่มขึ้นของประชากรเหยื่ออีกครั้ง ฯลฯ

แบบจำลองนี้มีลักษณะเฉพาะที่เรียกว่า "ความเสถียรที่เป็นกลาง" ซึ่งหมายความว่าประชากรจะเกิดวัฏจักรการแกว่งแบบเดียวกันโดยไม่มีกำหนด จนกว่าอิทธิพลภายนอกจะเปลี่ยนจำนวน หลังจากนั้นประชากรจะเกิดวัฏจักรการแกว่งใหม่ด้วยพารามิเตอร์ที่แตกต่างกัน เพื่อให้วัฏจักรมีเสถียรภาพ ประชากรต้องได้รับอิทธิพลจากภายนอก พยายามกลับไปสู่วงจรเดิมรอบดังกล่าว ตรงกันข้ามกับการแกว่งที่เสถียรอย่างเป็นกลางในแบบจำลอง Lotka-Volterra มักเรียกว่า รอบขีดจำกัดที่มั่นคง

อย่างไรก็ตาม แบบจำลอง Lotka-Volterra มีประโยชน์ตรงที่ช่วยให้เราแสดงให้เห็นถึงแนวโน้มหลักในความสัมพันธ์ระหว่างผู้ล่าและเหยื่อที่จะเกิดขึ้นในการผันผวนของวงจรคอนจูเกตในขนาดของประชากร

ย้อนกลับไปในยุค 20 A. Lotka และต่อมา V. Volterra เป็นอิสระจากเขา เสนอแบบจำลองทางคณิตศาสตร์ที่อธิบายความผันผวนของคอนจูเกตในประชากรของนักล่าและเหยื่อ ลองพิจารณารุ่น Lotka-Volterra รุ่นที่ง่ายที่สุด แบบจำลองนี้ขึ้นอยู่กับสมมติฐานหลายประการ:

1) ประชากรเหยื่อในกรณีที่ไม่มีนักล่าเพิ่มขึ้นแบบทวีคูณ

2) ความกดดันของผู้ล่าขัดขวางการเติบโตนี้

3) การตายของเหยื่อแปรผันตามความถี่ของการเผชิญหน้าระหว่างผู้ล่าและเหยื่อ (หรืออย่างอื่น แปรผันตามผลคูณของความหนาแน่นของประชากร)

4) อัตราการเกิดของนักล่าขึ้นอยู่กับความรุนแรงของการบริโภคเหยื่อ

อัตราการเปลี่ยนแปลงขนาดประชากรเหยื่อทันทีสามารถแสดงได้ด้วยสมการ

dN f /dt = r 1 N f - p 1 N f N x,

ที่ไหน r 1 - อัตราการเติบโตของประชากรของเหยื่อในทันทีโดยเฉพาะ p 1 - การเชื่อมต่อการตายของเหยื่อกับความหนาแน่นของนักล่าอย่างต่อเนื่อง เอ็น และ เอ็น เอ็กซ์ - ความหนาแน่นของเหยื่อและผู้ล่าตามลำดับ

อัตราการเติบโตทันทีของประชากรนักล่าในแบบจำลองนี้ถือว่าเท่ากับความแตกต่างระหว่างอัตราการเกิดและการตายคงที่:

dN x /dt = p 2 N x N x – d 2 N x,

ที่ไหนหน้า 2 - ค่าคงที่ที่เกี่ยวข้องกับอัตราการเกิดในประชากรนักล่ากับความหนาแน่นของเหยื่อ a d 2 - อัตราการตายของผู้ล่าโดยเฉพาะ

ตามสมการข้างต้น แต่ละประชากรที่มีปฏิสัมพันธ์ในการเพิ่มขึ้นจะถูกจำกัดโดยประชากรอื่นๆ เท่านั้น เช่น การเพิ่มขึ้นของจำนวนเหยื่อถูกจำกัดด้วยแรงกดดันของผู้ล่า และการเพิ่มจำนวนของผู้ล่านั้นถูกจำกัดด้วยจำนวนเหยื่อที่ไม่เพียงพอ ไม่มีการจำกัดจำนวนประชากรด้วยตนเอง เชื่อกันว่ามีอาหารเพียงพอสำหรับเหยื่อเสมอ ไม่คาดว่าประชากรเหยื่อจะหนีจากการควบคุมของนักล่า แม้ว่าในความเป็นจริงสิ่งนี้จะเกิดขึ้นค่อนข้างบ่อยก็ตาม

แม้จะมีรูปแบบทั่วไปของแบบจำลอง Lotka-Volterra แต่ก็สมควรได้รับความสนใจหากเพียงเพราะมันแสดงให้เห็นว่าแม้แต่ระบบปฏิสัมพันธ์ในอุดมคติระหว่างประชากรทั้งสองก็สามารถก่อให้เกิดพลวัตที่ค่อนข้างซับซ้อนของตัวเลขได้ การแก้ระบบสมการเหล่านี้ช่วยให้เราสามารถกำหนดเงื่อนไขในการรักษาจำนวนคงที่ (สมดุล) ของแต่ละสปีชีส์ได้ ประชากรเหยื่อจะคงที่หากความหนาแน่นของผู้ล่าเท่ากับ r 1 /p 1 และเพื่อให้ประชากรนักล่าคงที่ ความหนาแน่นของเหยื่อจะต้องเท่ากับ d 2 /p 2 หากเราวาดความหนาแน่นของเหยื่อบนแกน x เอ็น และ , และตามลำดับ - ความหนาแน่นของนักล่า เอ็น เอ็กซ์จากนั้นเส้นไอโซไลน์ที่แสดงสภาวะคงที่ของผู้ล่าและเหยื่อจะเป็นเส้นตรงสองเส้นตั้งฉากกันและกับแกนพิกัด (รูปที่ 6, ก) สันนิษฐานว่าความหนาแน่นของเหยื่อต่ำกว่าค่าที่กำหนด (เท่ากับ d 2 /p 2) ความหนาแน่นของนักล่าจะลดลงเสมอและสูงกว่านั้นจะเพิ่มขึ้นเสมอ ดังนั้นความหนาแน่นของเหยื่อจะเพิ่มขึ้นหากความหนาแน่นของนักล่าต่ำกว่าค่าเท่ากับ r 1 / p 1 และลดลงหากอยู่เหนือค่านี้ จุดตัดของเส้นไอโซไลน์สอดคล้องกับสภาพของความอุดมสมบูรณ์ของผู้ล่าและเหยื่ออย่างต่อเนื่อง และจุดอื่นๆ บนระนาบของกราฟนี้เคลื่อนที่ไปตามวิถีปิด ซึ่งสะท้อนถึงความผันผวนอย่างสม่ำเสมอในความอุดมสมบูรณ์ของผู้ล่าและเหยื่อ (รูปที่ 6, ข)ช่วงของการสั่นถูกกำหนดโดยอัตราส่วนเริ่มต้นของความหนาแน่นของผู้ล่าและเหยื่อ ยิ่งใกล้กับจุดตัดของไอโซไลน์ วงกลมก็จะเล็กลงตามเวกเตอร์ และด้วยเหตุนี้ แอมพลิจูดของการแกว่งก็จะน้อยลงตามไปด้วย

ข้าว. 6. การแสดงออกแบบกราฟิกของแบบจำลอง Lotka-Voltaire สำหรับระบบล่าเหยื่อ

หนึ่งในความพยายามครั้งแรกเพื่อให้ได้ความผันผวนของจำนวนผู้ล่าและเหยื่อในการทดลองในห้องปฏิบัติการเป็นของ G.F. เกาส์. วัตถุของการทดลองเหล่านี้คือพารามีเซียมซิลิเอต (พารามีเซียม หาง) และดิดิเนียมซิลิเอตนักล่า (ดิดิเนียม นสุทัม). อาหารของพารามีเซียมคือการเติมแบคทีเรียแขวนลอยลงในอาหารเป็นประจำ และดิดิเนียมกินเฉพาะพารามีเซียมเท่านั้น ระบบนี้กลับกลายเป็นว่าไม่เสถียรอย่างยิ่ง: ความกดดันของนักล่าเมื่อจำนวนของมันเพิ่มขึ้นนำไปสู่การกำจัดเหยื่อโดยสิ้นเชิงหลังจากนั้นประชากรของนักล่าก็ตายไป ทำให้การทดลองซับซ้อนขึ้น Gause ได้จัดที่พักพิงสำหรับเหยื่อโดยนำใยแก้วเล็กน้อยเข้าไปในหลอดทดลองที่มีซิลิเอต ปารามีเซียสามารถเคลื่อนไหวได้อย่างอิสระท่ามกลางเส้นด้ายสำลี แต่ดิดิเนียมทำไม่ได้ ในการทดลองเวอร์ชันนี้ ดิดิเนียมกินพารามีเซียทั้งหมดที่ลอยอยู่ในส่วนที่ไม่มีสำลีของหลอดทดลองและตายไป จากนั้นประชากรพารามีเซียก็กลับคืนมาเนื่องจากการแพร่พันธุ์ของบุคคลที่รอดชีวิตในสถานสงเคราะห์ เกาส์สามารถบรรลุความผันผวนของจำนวนผู้ล่าและเหยื่อได้ก็ต่อเมื่อเขาแนะนำทั้งเหยื่อและผู้ล่าเข้าสู่วัฒนธรรมเป็นครั้งคราว ซึ่งเป็นการจำลองการอพยพ

40 ปีหลังจากงานของเกาส์ การทดลองของเขาถูกทำซ้ำโดยแอล. ลัคคินบิล ซึ่งใช้ซิลิเอตเป็นเหยื่อ พารามีเซียม ออเรเลีย, และในฐานะนักล่าเช่นเดียวกัน ดิดิเนียม นสุทัม. Luckinbill สามารถจัดการความผันผวนของจำนวนประชากรเหล่านี้ได้หลายรอบ แต่เฉพาะในกรณีที่ความหนาแน่นของพารามีเซียมถูกจำกัดด้วยการขาดอาหาร (แบคทีเรีย) และเมทิลเซลลูโลสถูกเติมลงในของเหลวทางวัฒนธรรม - สารที่ช่วยลด ความเร็วในการเคลื่อนที่ของทั้งผู้ล่าและเหยื่อจึงลดความถี่ในการประชุมที่เป็นไปได้ ปรากฎว่าการสั่นระหว่างผู้ล่าและเหยื่อทำได้ง่ายกว่าหากปริมาตรของภาชนะทดลองเพิ่มขึ้น แม้ว่าในกรณีนี้เงื่อนไขของการจำกัดอาหารของเหยื่อก็จำเป็นเช่นกัน หากมีการเพิ่มอาหารส่วนเกินเข้าไปในระบบของผู้ล่าและเหยื่อที่อยู่ร่วมกันในโหมดการสั่น การตอบสนองก็คือจำนวนเหยื่อที่เพิ่มขึ้นอย่างรวดเร็ว ตามมาด้วยจำนวนผู้ล่าที่เพิ่มขึ้น ซึ่งนำไปสู่การกำจัดโดยสิ้นเชิง ประชากรเหยื่อ

แบบจำลอง Lotka และ Volterra ทำหน้าที่เป็นแรงผลักดันในการพัฒนาแบบจำลองอื่นๆ ของระบบล่าเหยื่อที่สมจริงยิ่งขึ้น โดยเฉพาะอย่างยิ่งแบบจำลองกราฟิกที่ค่อนข้างเรียบง่ายที่วิเคราะห์อัตราส่วนของไอโซไลน์ของเหยื่อที่แตกต่างกัน นักล่า ถูกเสนอโดย M. Rosenzweig และ R. MacArthur (Rosenzweig, MacArthur) ตามที่ผู้เขียนเหล่านี้เครื่องเขียน ( = ค่าคงที่) จำนวนเหยื่อในแกนพิกัดของความหนาแน่นของผู้ล่าและเหยื่อสามารถแสดงในรูปแบบของไอโซไลน์นูน (รูปที่ 7, a) จุดหนึ่งที่เส้นไอโซไลน์ตัดกับเส้นความหนาแน่นของเหยื่อสอดคล้องกับความหนาแน่นของเหยื่อขั้นต่ำที่อนุญาต (ประชากรด้านล่างมีความเสี่ยงสูงมากที่จะสูญพันธุ์ หากเพียงเพราะความถี่ของการพบกันระหว่างตัวผู้และตัวเมียต่ำ) และอีกจุดหนึ่ง สอดคล้องกับค่าสูงสุดที่กำหนดโดยปริมาณอาหารที่มีอยู่หรือลักษณะพฤติกรรมของเหยื่อเอง ให้เราย้ำว่าเรายังคงพูดถึงความหนาแน่นขั้นต่ำและสูงสุดในกรณีที่ไม่มีผู้ล่า เมื่อนักล่าปรากฏตัวและจำนวนของมันเพิ่มขึ้นความหนาแน่นของเหยื่อขั้นต่ำที่อนุญาตควรสูงขึ้นอย่างเห็นได้ชัดและค่าสูงสุด - ต่ำกว่า แต่ละค่าของความหนาแน่นของเหยื่อจะต้องสอดคล้องกับความหนาแน่นของนักล่าที่แน่นอนซึ่งทำให้ประชากรเหยื่อมีความคงที่ ตำแหน่งทางเรขาคณิตของจุดดังกล่าวคือไอโซไลน์ของเหยื่อในพิกัดความหนาแน่นของผู้ล่าและเหยื่อ เวกเตอร์ที่แสดงทิศทางของการเปลี่ยนแปลงความหนาแน่นของเหยื่อ (ในแนวนอน) มีทิศทางที่แตกต่างกันในด้านต่างๆ ของไอโซไคลน์ (รูปที่ 7a)

ข้าว. 7. ไอโซลินของประชากรเหยื่อ (a) และผู้ล่า (b) ที่อยู่นิ่ง

สำหรับนักล่านั้น ไอโซไลน์ก็ถูกสร้างขึ้นในพิกัดเดียวกันซึ่งสอดคล้องกับสถานะคงที่ของประชากร เวกเตอร์ที่แสดงทิศทางการเปลี่ยนแปลงของความอุดมสมบูรณ์ของสัตว์นักล่าจะถูกวางทิศทางขึ้นหรือลง ขึ้นอยู่กับด้านของไอโซไลน์ที่พวกมันอยู่ รูปร่างของไอโซไลน์นักล่าดังแสดงในรูปที่ 1 7, ข.ถูกกำหนดโดยประการแรกโดยการปรากฏตัวของเหยื่อที่มีความหนาแน่นขั้นต่ำซึ่งเพียงพอที่จะรักษาจำนวนประชากรของนักล่า (ที่ความหนาแน่นของเหยื่อที่ต่ำกว่านักล่าจะไม่สามารถเพิ่มจำนวนได้) และประการที่สองโดยการมีอยู่ของ ความหนาแน่นสูงสุดของนักล่านั้นเอง ซึ่งเกินกว่าจำนวนนั้นจะลดลงอย่างเป็นอิสระจากจำนวนเหยื่อที่มีอยู่มากมาย

ข้าว. 8. การเกิดขึ้นของโหมดการสั่นในระบบล่าเหยื่อขึ้นอยู่กับตำแหน่งของไอโซไลน์ของผู้ล่าและเหยื่อ

เมื่อรวมเหยื่อและผู้ล่าเข้าด้วยกันบนกราฟเดียว จะมีตัวเลือกที่แตกต่างกันสามแบบ (รูปที่ 8) ถ้าไอโซไลน์ของนักล่าตัดกับไอโซไลน์ของเหยื่อในตำแหน่งที่มันลดลงแล้ว (ที่เหยื่อมีความหนาแน่นสูง) พาหะที่แสดงการเปลี่ยนแปลงในจำนวนผู้ล่าและเหยื่อจะสร้างวิถีโคจรที่บิดเข้าด้านใน ซึ่งสอดคล้องกับความผันผวนที่หน่วงของความอุดมสมบูรณ์ ของเหยื่อและผู้ล่า (รูปที่ 8, A) ในกรณีที่ไอโซไลน์นักล่าตัดกับไอโซไลน์ของเหยื่อในส่วนที่ขึ้น (เช่น ในพื้นที่ ค่าต่ำความหนาแน่นของเหยื่อ) เวกเตอร์สร้างวิถีการคลี่คลายและความผันผวนของจำนวนผู้ล่าและเหยื่อเกิดขึ้นตามลำดับเมื่อแอมพลิจูดเพิ่มขึ้น (รูปที่ 8, ข)หากไอโซไลน์ของนักล่าตัดกับไอโซไลน์ของเหยื่อในบริเวณปลายของมัน เวกเตอร์จะก่อตัวเป็นวงกลมปิด และความผันผวนของจำนวนเหยื่อและผู้ล่านั้นมีลักษณะเฉพาะด้วยแอมพลิจูดและคาบที่มั่นคง (รูปที่ 8, วี)

กล่าวอีกนัยหนึ่ง การแกว่งแบบหน่วงนั้นสอดคล้องกับสถานการณ์ที่ผู้ล่ามีผลกระทบที่เห็นได้ชัดเจนต่อจำนวนเหยื่อที่มีความหนาแน่นสูงมากเท่านั้น (ใกล้กับค่าสูงสุด) และการแกว่งของแอมพลิจูดที่เพิ่มขึ้นเกิดขึ้นเมื่อผู้ล่าสามารถ เพิ่มจำนวนอย่างรวดเร็วแม้จะมีเหยื่อที่มีความหนาแน่นต่ำและมีวิธีทำลายมันอย่างรวดเร็ว ในแบบจำลองเวอร์ชันอื่น Posenzweig และ McArthur แสดงให้เห็นว่าการสั่นของนักล่าและเหยื่อสามารถทำให้เสถียรได้โดยการแนะนำ "ที่หลบภัย" กล่าวคือ บ่งบอกว่าในพื้นที่ที่มีเหยื่อหนาแน่นน้อยจะมีบริเวณที่เหยื่อมีความอุดมสมบูรณ์เพิ่มขึ้นโดยไม่คำนึงถึงจำนวนผู้ล่าที่มีอยู่

ความปรารถนาที่จะสร้างแบบจำลองที่สมจริงยิ่งขึ้นโดยการเพิ่มความซับซ้อนนั้นได้แสดงออกมาในผลงานของไม่เพียงแต่นักทฤษฎีเท่านั้น แต่ยังรวมถึง ผู้ทดลอง โดยเฉพาะอย่างยิ่ง Huffaker ได้รับผลลัพธ์ที่น่าสนใจซึ่งแสดงให้เห็นถึงความเป็นไปได้ของการอยู่ร่วมกันของนักล่าและเหยื่อในโหมดการสั่นโดยใช้ตัวอย่างของไรกินพืชขนาดเล็ก อีโอเตตรานีคัส เซ็กซ์มาคูลาทัสและมีเห็บนักล่ามาโจมตีเขา ไทฟิลโดรมัส ตะวันตก. ส้มที่วางอยู่บนถาดที่มีรู (เช่นเดียวกับที่ใช้เก็บและขนไข่) ถูกนำมาใช้เป็นอาหารของไรที่กินพืชเป็นอาหาร เวอร์ชันดั้งเดิมมี 40 รูบนถาดเดียว บางถาดมีส้ม (ปอกเปลือกบางส่วน) และบางถาดมีลูกบอลยาง เห็บทั้งสองชนิดแพร่พันธุ์ได้เร็วมาก ดังนั้นธรรมชาติของการเปลี่ยนแปลงของประชากรจึงสามารถเปิดเผยได้ในระยะเวลาอันสั้น เมื่อวางไรเพศเมีย 20 ตัวลงบนถาด Huffaker สังเกตเห็นการเติบโตอย่างรวดเร็วของประชากรซึ่งมีความเสถียรที่ระดับ 5-8,000 ตัว (ต่อส้ม) หากนักล่าหลายคนถูกเพิ่มเข้าไปในจำนวนเหยื่อที่เพิ่มขึ้น จำนวนประชากรของเหยื่อกลุ่มหลังก็จะเพิ่มขึ้นอย่างรวดเร็วและตายไปเมื่อเหยื่อทั้งหมดถูกกิน

ด้วยการเพิ่มขนาดของถาดเป็น 120 รู โดยสุ่มส้มแต่ละผลกระจายไปตามลูกบอลยางหลายๆ ลูก Huffaker จึงสามารถยืดเวลาการอยู่ร่วมกันของผู้ล่าและเหยื่อได้ เมื่อปรากฎอัตราส่วนของอัตราการแพร่กระจายของพวกมันมีบทบาทสำคัญในปฏิสัมพันธ์ระหว่างผู้ล่าและเหยื่อ ฮัฟเฟเกอร์แนะนำว่าการทำให้เหยื่อเคลื่อนไหวได้ง่ายขึ้นและการเคลื่อนไหวของนักล่ายากขึ้น จะทำให้ระยะเวลาอยู่ร่วมกันของพวกมันยาวนานขึ้น ในการทำเช่นนี้บนถาด 120 หลุม สุ่มวางส้ม 6 ลูกไว้ท่ามกลางลูกบอลยาง และรอบๆ หลุมที่มีส้ม วาสลีนได้ถูกสร้างขึ้นเพื่อป้องกันไม่ให้ผู้ล่าแพร่กระจาย และหมุดไม้ก็เพื่อความสะดวกในการตั้งถิ่นฐานของเหยื่อ เสริมความแข็งแกร่งบนถาดซึ่งทำหน้าที่เป็น "แผ่นบินขึ้น" สำหรับไรที่กินพืชเป็นอาหาร (ความจริงก็คือสายพันธุ์นี้ผลิตเส้นไหมบาง ๆ และด้วยความช่วยเหลือจากพวกมันสามารถลอยอยู่ในอากาศกระจายไปตามลม) ในแหล่งที่อยู่อาศัยที่ซับซ้อนเช่นนี้ ผู้ล่าและเหยื่ออยู่ร่วมกันเป็นเวลา 8 เดือน แสดงให้เห็นถึงความผันผวนของประชากรครบสามรอบ เงื่อนไขที่สำคัญที่สุดสำหรับการอยู่ร่วมกันนี้มีดังต่อไปนี้: ความหลากหลายของแหล่งที่อยู่อาศัย (ในแง่ของการมีอยู่ของพื้นที่ที่เหมาะสมและไม่เหมาะสมสำหรับเหยื่อที่จะอาศัยอยู่) เช่นเดียวกับความเป็นไปได้ของการย้ายถิ่นของเหยื่อและผู้ล่า (ในขณะที่ยังคงรักษา ข้อได้เปรียบของเหยื่อบางประการในเรื่องความเร็วของกระบวนการนี้) กล่าวอีกนัยหนึ่งผู้ล่าสามารถกำจัดเหยื่อที่สะสมอยู่ในท้องถิ่นได้อย่างสมบูรณ์ แต่เหยื่อบางคนจะมีเวลาในการอพยพและก่อให้เกิดการสะสมในท้องถิ่นอื่น ๆ ไม่ช้าก็เร็วนักล่าก็จะไปถึงการสะสมในท้องถิ่นใหม่ แต่ในระหว่างนี้เหยื่อจะมีเวลาไปตั้งถิ่นฐานในสถานที่อื่น (รวมถึงที่ที่มันเคยอาศัยอยู่มาก่อน แต่ถูกกำจัดออกไปแล้ว)

สิ่งที่คล้ายคลึงกับสิ่งที่ Huffaker สังเกตในการทดลองก็เกิดขึ้นในสภาพธรรมชาติเช่นกัน เช่น ผีเสื้อกลางคืนกระบองเพชร (กระบองเพชร ต้นกระบองเพชร), นำมาออสเตรเลียลดจำนวนกระบองเพชรแพร์เต็มไปด้วยหนามลงอย่างมาก แต่ไม่ได้ทำลายมันอย่างแม่นยำเพราะกระบองเพชรจะแพร่กระจายเร็วขึ้นเล็กน้อย ในสถานที่เหล่านั้นซึ่งกำจัดลูกแพร์เต็มไปด้วยหนามมอดก็จะไม่เกิดขึ้น ดังนั้นเมื่อผ่านไประยะหนึ่งเมื่อลูกแพร์เต็มไปด้วยหนามแทรกซึมมาที่นี่อีกครั้งก็สามารถเติบโตได้ในช่วงระยะเวลาหนึ่งโดยไม่เสี่ยงต่อการถูกมอดทำลาย อย่างไรก็ตามเมื่อเวลาผ่านไปมอดก็ปรากฏขึ้นที่นี่อีกครั้งและเมื่อขยายพันธุ์อย่างรวดเร็วก็ทำลายลูกแพร์เต็มไปด้วยหนาม

เมื่อพูดถึงความผันผวนของนักล่าและเหยื่อ เราไม่สามารถพลาดที่จะพูดถึงการเปลี่ยนแปลงของวัฏจักรของจำนวนกระต่ายและแมวป่าชนิดหนึ่งในแคนาดา ซึ่งติดตามตามสถิติการเก็บเกี่ยวขนสัตว์โดยบริษัท Hudson Bay ตั้งแต่ปลายศตวรรษที่ 18 ถึงต้นศตวรรษที่ 19 ศตวรรษที่ 20. ตัวอย่างนี้มักถูกมองว่าเป็นตัวอย่างคลาสสิกของการแกว่งของเหยื่อระหว่างผู้ล่า แม้ว่าในความเป็นจริงเราจะเห็นเพียงการเติบโตของจำนวนผู้ล่า (แมวป่าชนิดหนึ่ง) ตามการเติบโตของประชากรเหยื่อ (กระต่าย) สำหรับจำนวนกระต่ายที่ลดลงหลังจากการเพิ่มขึ้นแต่ละครั้งนั้นไม่สามารถอธิบายได้ด้วยแรงกดดันที่เพิ่มขึ้นของผู้ล่าเท่านั้น แต่มีความเกี่ยวข้องกับปัจจัยอื่น ๆ ซึ่งเห็นได้ชัดว่าขาดอาหารในฤดูหนาวเป็นหลัก โดยเฉพาะอย่างยิ่ง M. Gilpin ได้ข้อสรุปนี้ ซึ่งพยายามตรวจสอบว่าแบบจำลอง Lotka-Volterra แบบคลาสสิกสามารถอธิบายข้อมูลเหล่านี้ได้หรือไม่ ผลการทดสอบแสดงให้เห็นว่าไม่มีความพอดีที่น่าพอใจกับแบบจำลอง แต่น่าแปลกที่จะดีกว่าหากสลับผู้ล่าและเหยื่อเข้าด้วยกัน เช่น ตีความแมวป่าชนิดหนึ่งว่าเป็น "เหยื่อ" และกระต่ายเป็น "นักล่า" สถานการณ์ที่คล้ายกันนี้สะท้อนให้เห็นในชื่อบทความที่น่าขบขัน (“ กระต่ายกินแมวป่าชนิดหนึ่งหรือไม่?”) ซึ่งโดยพื้นฐานแล้วมีความจริงจังมากและตีพิมพ์ในวารสารวิทยาศาสตร์ที่จริงจัง

บ่อยครั้งสมาชิกของสปีชีส์หนึ่ง (ประชากร) กินสมาชิกของสปีชีส์อื่นเป็นอาหาร

แบบจำลอง Lotka-Volterra เป็นแบบจำลองของการดำรงอยู่ร่วมกันของประชากรสองคนประเภท "นักล่า - เหยื่อ"

แบบจำลองนักล่า-เหยื่อได้รับการพัฒนาครั้งแรกโดย A. Lotka ในปี 1925 ซึ่งใช้แบบจำลองนี้เพื่ออธิบายพลวัตของการมีปฏิสัมพันธ์ระหว่างประชากรทางชีววิทยา ในปี 1926 โดยเป็นอิสระจาก Lotka แบบจำลองที่คล้ายกัน (และซับซ้อนกว่า) ได้รับการพัฒนาโดยนักคณิตศาสตร์ชาวอิตาลี V. Volterra ซึ่งมีการวิจัยเชิงลึกในสาขานี้ ปัญหาสิ่งแวดล้อมวางรากฐานสำหรับทฤษฎีทางคณิตศาสตร์ของชุมชนทางชีววิทยาหรือที่เรียกว่า นิเวศวิทยาทางคณิตศาสตร์

ใน รูปแบบทางคณิตศาสตร์ระบบสมการที่เสนอมีรูปแบบดังนี้

โดยที่ x คือจำนวนเหยื่อ y คือจำนวนผู้ล่า t คือเวลา α, β, γ, δ คือสัมประสิทธิ์ที่สะท้อนถึงปฏิสัมพันธ์ระหว่างประชากร

การกำหนดปัญหา

พิจารณาพื้นที่ปิดซึ่งมีประชากรสองกลุ่ม ได้แก่ สัตว์กินพืช (“เหยื่อ”) และผู้ล่า เชื่อกันว่าไม่มีการนำเข้าหรือส่งออกสัตว์และมีอาหารเพียงพอสำหรับสัตว์กินพืช จากนั้นสมการการเปลี่ยนแปลงจำนวนเหยื่อ (เฉพาะเหยื่อ) จะอยู่ในรูปแบบ:

โดยที่ $α$ คืออัตราการเกิดของเหยื่อ

$x$ คือขนาดของประชากรเหยื่อ

$\frac(dx)(dt)$ คืออัตราการเติบโตของประชากรเหยื่อ

เมื่อผู้ล่าไม่ล่า พวกมันอาจสูญพันธุ์ได้ ซึ่งหมายความว่าสมการสำหรับจำนวนผู้ล่า (เฉพาะผู้ล่า) จะกลายเป็น:

โดยที่ $γ$ คืออัตราการสูญเสียของผู้ล่า

$y$ คือขนาดของประชากรนักล่า

$\frac(dy)(dt)$ คืออัตราการเติบโตของประชากรนักล่า

เมื่อผู้ล่าและเหยื่อพบกัน (ความถี่ของการประชุมเป็นสัดส่วนโดยตรงกับผลิตภัณฑ์) ผู้ล่าจะทำลายเหยื่อด้วยค่าสัมประสิทธิ์ ผู้ล่าที่ได้รับอาหารอย่างดีสามารถสืบพันธุ์ลูกหลานโดยมีค่าสัมประสิทธิ์ ดังนั้นระบบสมการของแบบจำลองจะอยู่ในรูปแบบ:

การแก้ปัญหา

เรามาสร้างแบบจำลองทางคณิตศาสตร์ของการอยู่ร่วมกันของประชากรทางชีววิทยาสองคนประเภท "นักล่า-เหยื่อ" กัน

ปล่อยให้ประชากรทางชีววิทยาสองคนอาศัยอยู่ร่วมกันในสภาพแวดล้อมที่แยกจากกัน สภาพแวดล้อมมีความนิ่งและให้ทุกสิ่งที่จำเป็นสำหรับชีวิตของเหยื่อประเภทใดประเภทหนึ่งอย่างไม่จำกัด อีกสายพันธุ์หนึ่ง - ผู้ล่า - อาศัยอยู่ในสภาวะนิ่ง แต่กินเหยื่อเท่านั้น แมว หมาป่า หอก สุนัขจิ้งจอกสามารถทำหน้าที่เป็นผู้ล่าได้ ส่วนไก่ กระต่าย ปลาคาร์พไม้กางเขน และหนูสามารถทำหน้าที่เป็นเหยื่อได้ ตามลำดับ

หากจะให้เจาะจง ให้ถือว่าแมวเป็นผู้ล่า และไก่เป็นเหยื่อ

ดังนั้น ไก่และแมวจึงอาศัยอยู่ในพื้นที่ห่างไกล เช่น ลานฟาร์ม สภาพแวดล้อมให้อาหารไก่ไม่จำกัด ส่วนแมวกินเฉพาะไก่เท่านั้น ให้เราแสดงโดย

$x$ – จำนวนไก่

$у$ – จำนวนแมว

เมื่อเวลาผ่านไป จำนวนไก่และแมวเปลี่ยนแปลงไป แต่เราจะถือว่า $x$ และ $y$ เป็นฟังก์ชันต่อเนื่องของเวลา t ลองเรียกตัวเลขคู่หนึ่งว่า $x, y)$ สถานะของโมเดล

มาดูกันว่าสถานะของโมเดล $(x, y).$ เปลี่ยนแปลงไปอย่างไร

ลองพิจารณา $\frac(dx)(dt)$ – อัตราการเปลี่ยนแปลงของจำนวนไก่

หากไม่มีแมว จำนวนไก่ก็จะเพิ่มมากขึ้น และยิ่งเร็วเท่าไรก็ยิ่งมีจำนวนไก่มากขึ้นเท่านั้น เราจะถือว่าการพึ่งพานั้นเป็นเส้นตรง:

$\frac(dx)(dt) a_1 x$,

$a_1$ เป็นค่าสัมประสิทธิ์ที่ขึ้นอยู่กับสภาพความเป็นอยู่ของไก่ อัตราตายตามธรรมชาติ และอัตราการเกิดของไก่เท่านั้น

$\frac(dy)(dt)$ – อัตราการเปลี่ยนแปลงของจำนวนแมว (หากไม่มีไก่) ขึ้นอยู่กับจำนวนแมว y

หากไม่มีไก่ จำนวนแมวก็จะลดลง (ไม่มีอาหาร) และพวกมันก็จะตายไป เราจะถือว่าการพึ่งพานั้นเป็นเส้นตรง:

$\frac(dy)(dt) - a_2 y$.

ในระบบนิเวศ อัตราการเปลี่ยนแปลงจำนวนของแต่ละสายพันธุ์จะถือเป็นสัดส่วนกับปริมาณของมันด้วย แต่จะมีค่าสัมประสิทธิ์เท่านั้นที่ขึ้นอยู่กับจำนวนบุคคลในสายพันธุ์อื่น ดังนั้น สำหรับไก่ ค่าสัมประสิทธิ์นี้จะลดลงตามจำนวนแมวที่เพิ่มขึ้น และสำหรับแมว ค่าสัมประสิทธิ์นี้จะเพิ่มขึ้นตามจำนวนไก่ที่เพิ่มขึ้น เราจะถือว่าการพึ่งพานั้นเป็นเส้นตรงด้วย จากนั้นเราจะได้ระบบสมการเชิงอนุพันธ์:

ระบบสมการนี้เรียกว่าแบบจำลองโวลแตร์รา-ลอตกา

a1, a2, b1, b2 – ค่าสัมประสิทธิ์ตัวเลข ซึ่งเรียกว่าพารามิเตอร์โมเดล

อย่างที่คุณเห็นลักษณะของการเปลี่ยนแปลงสถานะของโมเดล (x, y) จะถูกกำหนดโดยค่าของพารามิเตอร์ ด้วยการเปลี่ยนพารามิเตอร์เหล่านี้และการแก้ระบบสมการแบบจำลอง ทำให้สามารถศึกษารูปแบบของการเปลี่ยนแปลงในสถานะของระบบนิเวศได้

การใช้โปรแกรม MATLAB ระบบสมการ Lotka-Volterra ได้รับการแก้ไขดังนี้

ในรูป ภาพที่ 1 แสดงวิธีแก้ปัญหาของระบบ วิธีแก้ปัญหาจะแตกต่างกันไปขึ้นอยู่กับเงื่อนไขเริ่มต้น สีที่ต่างกันวิถี

ในรูป 2 นำเสนอวิธีแก้ปัญหาเดียวกัน แต่คำนึงถึงแกนเวลา t (นั่นคือ มีการขึ้นอยู่กับเวลา)

แบบจำลองปฏิสัมพันธ์สองประเภท

สมมติฐานของโวลแตร์รา การเปรียบเทียบกับจลนพลศาสตร์เคมี แบบจำลองปฏิสัมพันธ์ของโวลแตร์รา การจำแนกประเภทของปฏิสัมพันธ์ การแข่งขัน นักล่าเหยื่อ แบบจำลองทั่วไปของการโต้ตอบของสายพันธุ์ . แบบจำลองโคลโมโกรอฟ แบบจำลองปฏิสัมพันธ์ของแมคอาเธอร์ระหว่างแมลงสองสายพันธุ์ พาราเมตริก และภาพบุคคลของระบบ Bazykin

ผู้ก่อตั้งทฤษฎีทางคณิตศาสตร์สมัยใหม่ของประชากรได้รับการพิจารณาอย่างถูกต้องว่าเป็นนักคณิตศาสตร์ชาวอิตาลี Vito Volterra ผู้พัฒนาทฤษฎีทางคณิตศาสตร์ของชุมชนทางชีววิทยาซึ่งมีเครื่องมือคือสมการเชิงอนุพันธ์และปริพันธ์ - ดิฟเฟอเรนเชียล(Vito Volterra Lecons sur la Theorie Mathematique de la Lutte pour la Vie ปารีส, 1931) ในทศวรรษต่อมา พลวัตของประชากรพัฒนาขึ้นตามแนวคิดที่แสดงในหนังสือเล่มนี้เป็นหลัก หนังสือของ Volterra แปลภาษารัสเซียตีพิมพ์ในปี 1976 ภายใต้ชื่อ: “ ทฤษฎีทางคณิตศาสตร์ต่อสู้เพื่อการดำรงอยู่” โดยมีคำตามหลังโดย Yu.M. Svirezhev ซึ่งตรวจสอบประวัติความเป็นมาของการพัฒนานิเวศวิทยาทางคณิตศาสตร์ในช่วงปี 1931–1976

หนังสือของโวลแตร์ราเขียนขึ้นในลักษณะเดียวกับการเขียนหนังสือเกี่ยวกับคณิตศาสตร์ ขั้นแรกจะกำหนดสมมติฐานบางประการเกี่ยวกับวัตถุทางคณิตศาสตร์ที่ควรศึกษา จากนั้นจึงดำเนินการศึกษาทางคณิตศาสตร์เกี่ยวกับคุณสมบัติของวัตถุเหล่านี้

ระบบที่ Volterra ศึกษาประกอบด้วยสองประเภทขึ้นไป ในบางกรณีอาจพิจารณาการจัดหาอาหารที่ใช้ด้วย สมการที่อธิบายปฏิสัมพันธ์ของประเภทเหล่านี้จะขึ้นอยู่กับแนวคิดต่อไปนี้

สมมติฐานของโวลแตร์รา

1. อาหารมีจำหน่ายในปริมาณไม่จำกัด หรือมีการควบคุมอุปทานอย่างเข้มงวดเมื่อเวลาผ่านไป

2. บุคคลของแต่ละสายพันธุ์ตายในลักษณะที่สัดส่วนคงที่ของบุคคลที่มีอยู่ตายต่อหน่วยเวลา

3. สัตว์นักล่ากินเหยื่อ และต่อหน่วยเวลา จำนวนเหยื่อที่ถูกกินจะเป็นสัดส่วนเสมอกับความน่าจะเป็นที่จะได้พบกับบุคคลของทั้งสองสายพันธุ์นี้ กล่าวคือ ผลคูณของจำนวนผู้ล่าและจำนวนเหยื่อ

4. หากมีอาหารในปริมาณจำกัดและมีหลายสายพันธุ์ที่สามารถบริโภคได้ ส่วนแบ่งของอาหารที่บริโภคโดยหนึ่งสายพันธุ์ต่อหน่วยเวลาจะเป็นสัดส่วนกับจำนวนบุคคลของสายพันธุ์นี้ โดยคำนึงถึงค่าสัมประสิทธิ์ที่แน่นอนขึ้นอยู่กับ สายพันธุ์ (รูปแบบของการแข่งขันแบบเฉพาะเจาะจง)

5. หากสายพันธุ์ใดกินอาหารที่มีอยู่ในปริมาณไม่จำกัด การเพิ่มจำนวนชนิดต่อหน่วยเวลาจะเป็นสัดส่วนกับจำนวนชนิดนั้น

6. หากสายพันธุ์กินอาหารที่มีอยู่ในปริมาณที่จำกัด การสืบพันธุ์ของมันจะถูกควบคุมโดยอัตราการบริโภคอาหาร เช่น ต่อหน่วยเวลาเพิ่มขึ้นจะเป็นสัดส่วนกับปริมาณอาหารที่รับประทาน

การเปรียบเทียบกับจลนพลศาสตร์เคมี

สมมติฐานเหล่านี้มีความคล้ายคลึงกันอย่างใกล้ชิดกับจลนพลศาสตร์เคมี ในสมการพลศาสตร์ประชากร เช่นเดียวกับในสมการจลนศาสตร์เคมี จะใช้ "หลักการชนกัน" เมื่ออัตราการเกิดปฏิกิริยาเป็นสัดส่วนกับผลคูณของความเข้มข้นของส่วนประกอบที่ทำปฏิกิริยา

ตามสมมติฐานของโวลแตร์รา ความเร็วกระบวนการ การสูญพันธุ์ของแต่ละชนิดจะแปรผันตามจำนวนชนิด ในจลนศาสตร์เคมี สิ่งนี้สอดคล้องกับปฏิกิริยาโมเลกุลเดี่ยวของการสลายตัวของสารบางชนิด และในแบบจำลองทางคณิตศาสตร์ มันสอดคล้องกับพจน์เชิงเส้นเชิงลบทางด้านขวาของสมการ

ตามแนวคิดของจลนศาสตร์เคมี อัตราของปฏิกิริยาสองโมเลกุลของอันตรกิริยาระหว่างสารทั้งสองนั้นแปรผันตามความน่าจะเป็นของการชนกันของสารเหล่านี้ เช่น ผลคูณของความเข้มข้นของพวกเขา ในทำนองเดียวกัน ตามสมมติฐานของโวลแตร์รา อัตราการแพร่พันธุ์ของผู้ล่า (การตายของเหยื่อ) นั้นเป็นสัดส่วนกับความน่าจะเป็นของการเผชิญหน้าระหว่างผู้ล่าและเหยื่อ กล่าวคือ ผลคูณของตัวเลขของพวกเขา ในทั้งสองกรณี คำศัพท์แบบไบลิเนียร์จะปรากฏในระบบแบบจำลองทางด้านขวามือของสมการที่เกี่ยวข้อง

สุดท้าย พจน์เชิงบวกเชิงเส้นทางด้านขวามือของสมการโวลแตร์รา ซึ่งสอดคล้องกับการเติบโตของประชากรภายใต้เงื่อนไขไม่จำกัด สอดคล้องกับเงื่อนไขการเร่งปฏิกิริยาอัตโนมัติ ปฏิกริยาเคมี. ความคล้ายคลึงกันของสมการในแบบจำลองทางเคมีและสิ่งแวดล้อมช่วยให้เราใช้วิธีการวิจัยเดียวกันสำหรับการสร้างแบบจำลองทางคณิตศาสตร์ของจลนพลศาสตร์ของประชากร เช่นเดียวกับระบบปฏิกิริยาเคมี

การจำแนกประเภทของปฏิสัมพันธ์

ตามสมมติฐานของโวลแตร์รา ปฏิสัมพันธ์ของสองสายพันธุ์ จำนวนที่ x 1 และ x 2 สามารถอธิบายได้ด้วยสมการ:

(9.1)

นี่คือพารามิเตอร์ ก ฉัน - ค่าคงที่ของอัตราการเติบโตของสายพันธุ์ ค ฉัน- ค่าคงที่ของการ จำกัด ตัวเองของตัวเลข (การแข่งขันภายในเฉพาะ) บีจ- ค่าคงที่ปฏิสัมพันธ์ของสายพันธุ์ (ฉัน, เจ= 1,2) สัญญาณของค่าสัมประสิทธิ์เหล่านี้จะกำหนดประเภทของการโต้ตอบ

ในวรรณกรรมทางชีววิทยา ปฏิกิริยาระหว่างกันมักถูกจำแนกตามกลไกที่เกี่ยวข้อง ความหลากหลายที่นี่มีมหาศาล: ปฏิกิริยาทางโภชนาการต่าง ๆ ปฏิกิริยาทางเคมีที่มีอยู่ระหว่างแบคทีเรียและ สาหร่ายแพลงก์ตอนปฏิกิริยาของเชื้อรากับสิ่งมีชีวิตอื่น การสืบทอดของสิ่งมีชีวิตในพืช ซึ่งสัมพันธ์กันโดยเฉพาะกับการแข่งขัน แสงแดดและด้วยวิวัฒนาการของดินเป็นต้น การจำแนกประเภทนี้ดูกว้างใหญ่

อี . Odum โดยคำนึงถึงแบบจำลองที่เสนอโดย V. Volterra ได้เสนอการจำแนกประเภทไม่ใช่โดยกลไก แต่โดยผลลัพธ์ ตามการจำแนกประเภทนี้ ความสัมพันธ์ควรได้รับการประเมินว่าเป็นเชิงบวก ลบ หรือเป็นกลาง ขึ้นอยู่กับว่าความอุดมสมบูรณ์ของสายพันธุ์หนึ่งเพิ่มขึ้น ลดลง หรือยังคงไม่เปลี่ยนแปลงเมื่อมีสายพันธุ์อื่นอยู่ จากนั้นสามารถนำเสนอประเภทการโต้ตอบหลัก ๆ ในรูปแบบตารางได้

ประเภทของปฏิสัมพันธ์ของสายพันธุ์

ซิมบิโอซิส			ข 12 ,ข 21 >0
ความเห็นอกเห็นใจ			ข 12 ,>0, ข 21 =0
ผู้ล่า-เหยื่อ			ข 12 ,>0, ข 21 <0
การเสียสละ			ข 12 ,=0, ข 21 <0
การแข่งขัน			ข 12 , ข 21 <0
ความเป็นกลาง			ข 12 , ข 21 =0

คอลัมน์สุดท้ายแสดงสัญญาณของสัมประสิทธิ์ปฏิสัมพันธ์จากระบบ (9.1)

มาดูการโต้ตอบประเภทหลักๆ กัน

สมการแข่งขัน:

ดังที่เราเห็นในการบรรยายครั้งที่ 6 สมการการแข่งขันคือ:

(9.2)

โซลูชันระบบเครื่องเขียน:

(1).

ต้นกำเนิดของพิกัดสำหรับพารามิเตอร์ระบบใดๆ ถือเป็นโหนดที่ไม่เสถียร

(2). (9.3)

ค สภาพนิ่ง (9.3) เป็นอานที่ ก 1 >ข 12 /กับ 2 และ

โหนดเสถียรที่ ก 1 12 /วินาที 2 . เงื่อนไขนี้หมายความว่าสายพันธุ์จะสูญพันธุ์หากอัตราการเติบโตของมันน้อยกว่าค่าวิกฤตที่แน่นอน

(3). (9.4)

ค สารละลายคงที่ (9.4)¾ อานที่ ก 2 >ข 21 /ค 1 และโหนดที่เสถียรที่ ก 2< ข 21 /ค 1

(4). (9.5)

สถานะคงที่ (9.5) แสดงถึงลักษณะการอยู่ร่วมกันของสองสายพันธุ์ที่แข่งขันกัน และแสดงถึงโหนดที่เสถียรหากความสัมพันธ์เป็นที่พอใจ:

นี่แสดงถึงความไม่เท่าเทียมกัน:

ข 12 ข 21 1 ค 2 , (9.6)

ทำให้เรากำหนดเงื่อนไขการอยู่ร่วมกันของสิ่งมีชีวิตได้:

ผลคูณของสัมประสิทธิ์ปฏิสัมพันธ์ระหว่างประชากรน้อยกว่าผลคูณของสัมประสิทธิ์ภายในปฏิสัมพันธ์ของประชากร

แท้จริงแล้วให้พิจารณาอัตราการเติบโตตามธรรมชาติของทั้งสองสายพันธุ์ด้วยก 1 , ก 2 เหมือนกัน. จากนั้นเงื่อนไขที่จำเป็นสำหรับความมั่นคงจะเป็น

ค 2 > ข 12 ,ค 1 >ข 21 .

ความไม่เท่าเทียมกันเหล่านี้แสดงให้เห็นว่าการเพิ่มขนาดของคู่แข่งรายหนึ่งจะระงับการเติบโตของตนเองมากกว่าการเติบโตของคู่แข่งรายอื่น หากจำนวนของทั้งสองสายพันธุ์ถูกจำกัดบางส่วนหรือทั้งหมดด้วยทรัพยากรที่ต่างกัน ความไม่เท่าเทียมกันข้างต้นถือว่าใช้ได้ หากทั้งสองสายพันธุ์มีความต้องการที่เหมือนกันทุกประการ หนึ่งในนั้นจะมีศักยภาพมากกว่าและจะเข้ามาแทนที่คู่แข่ง

พฤติกรรมของวิถีเฟสของระบบให้แนวคิดที่ชัดเจนเกี่ยวกับผลลัพธ์ที่เป็นไปได้ของการแข่งขัน ให้เราถือเอาด้านขวามือของสมการของระบบ (9.2) เป็นศูนย์:

x 1 (ก 1 –ซี 1 x 1 – ข 12 x 2) = 0 (ดีเอ็กซ์ 1 /ดีที = 0),

x 2 (ก 2 –ข 21 x 1 – ค 2 x 2) = 0 (ดีเอ็กซ์ 2 /ดีที = 0),

ในกรณีนี้ เราได้สมการสำหรับไอโซไลน์หลักของระบบ

x 2 = – ข 21 x 1 / ค 2 +ก 2 /ค2, x 2 = 0

– สมการของไอโซไลน์ของแทนเจนต์แนวตั้ง

x 2 = – ค 1 x 1 /ข12+ ก 1 /ข 12 , x 1 = 0

– สมการของไอโซไลน์ของแทนเจนต์แนวตั้ง จุดตัดกันแบบคู่ของไอโซไลน์ของระบบแทนเจนต์แนวตั้งและแนวนอนแสดงถึงคำตอบคงที่ของระบบสมการ (9.2.) และพิกัด เป็นจำนวนคงที่ของสายพันธุ์ที่แข่งขันกัน

ตำแหน่งที่เป็นไปได้ของไอโซไลน์หลักในระบบ (9.2) จะแสดงในรูปที่ 9.1 ข้าว. 9.1กสอดคล้องกับความอยู่รอดของเผ่าพันธุ์x 1 มะเดื่อ 9.1 ข– ความอยู่รอดของเผ่าพันธุ์x 2 มะเดื่อ 9.1 วี– การอยู่ร่วมกันของชนิดพันธุ์เมื่อเป็นไปตามเงื่อนไข (9.6) รูปที่ 9.1ชสาธิตระบบทริกเกอร์ ผลลัพธ์ของการแข่งขันจะขึ้นอยู่กับเงื่อนไขเริ่มต้น สถานะคงที่ไม่เป็นศูนย์ (9.5) สำหรับทั้งสองประเภทไม่เสถียร นี่คืออานม้าที่เซพาราทริกซ์ผ่านไป เพื่อแยกพื้นที่การอยู่รอดของแต่ละสายพันธุ์

ข้าว. 9.1.ตำแหน่งของไอโซไลน์หลักบนเฟสแนวตั้งของระบบโวลแตร์ราของการแข่งขันสองประเภท (9.2) ด้วยอัตราส่วนของพารามิเตอร์ที่แตกต่างกัน คำอธิบายในข้อความ

เพื่อศึกษาการแข่งขันของสายพันธุ์ ได้ทำการทดลองกับสิ่งมีชีวิตหลากหลายชนิด โดยทั่วไปแล้ว สองสายพันธุ์ที่เกี่ยวข้องกันอย่างใกล้ชิดจะถูกเลือกและปลูกร่วมกันและแยกจากกันภายใต้เงื่อนไขที่มีการควบคุมอย่างเข้มงวด ในบางช่วงจะมีการดำเนินการสำรวจสำมะโนประชากรโดยสมบูรณ์หรือแบบคัดเลือก ข้อมูลจากการทดลองซ้ำหลายครั้งจะถูกบันทึกและวิเคราะห์ มีการศึกษาเกี่ยวกับโปรโตซัว (โดยเฉพาะ ciliates) แมลงปีกแข็งหลายชนิดในสกุล Tribolium แมลงหวี่ และสัตว์จำพวกครัสเตเชียนน้ำจืด (แดฟเนีย) มีการทดลองมากมายกับประชากรจุลินทรีย์ (ดูบรรยายที่ 11) การทดลองยังดำเนินการในธรรมชาติอีกด้วย ซึ่งรวมถึงสัตว์พลานาเรีย (เรย์โนลด์ส) มดสองสายพันธุ์ (ปอนติน) ฯลฯ ในรูป 9.2. แสดงให้เห็นกราฟการเจริญเติบโตของไดอะตอมโดยใช้ทรัพยากรเดียวกัน (ครอบครองช่องทางนิเวศน์เดียวกัน) เมื่อปลูกในเชิงเดี่ยวแอสเทอริโอเนลลา ฟอร์โมซา ถึงระดับความหนาแน่นคงที่และรักษาความเข้มข้นของทรัพยากร (ซิลิเกต) ไว้ที่ระดับต่ำอย่างต่อเนื่อง ข. เมื่อปลูกในเชิงเดี่ยวซินเนดราอูอินา มีพฤติกรรมคล้ายกันและรักษาความเข้มข้นของซิลิเกตให้อยู่ในระดับที่ต่ำกว่าอีกด้วย B. ระหว่างการเพาะปลูกร่วมกัน (ซ้ำกัน) Synedrauina เข้ามาแทนที่ Asterionella formosa น่าจะเป็นซินเนดรา

ข้าว. 9.2.การแข่งขันในไดอะตอม เอ -เมื่อปลูกในเชิงเดี่ยวแอสเทอริโอเนลลา ฟอร์โมซา ถึงระดับความหนาแน่นคงที่และรักษาความเข้มข้นของทรัพยากร (ซิลิเกต) ไว้ที่ระดับต่ำอย่างต่อเนื่อง ข -เมื่อปลูกในเชิงเดี่ยวซินเนดราอูอินา มีพฤติกรรมคล้ายกันและรักษาความเข้มข้นของซิลิเกตให้อยู่ในระดับที่ต่ำกว่าอีกด้วย วี -ด้วยการเพาะปลูกร่วมกัน (ซ้ำกัน) Synedruina เข้ามาแทนที่ Asterionella formosa น่าจะเป็นซินเนดรา ชนะการแข่งขันเนื่องจากความสามารถในการใช้วัสดุพิมพ์ได้อย่างเต็มที่ยิ่งขึ้น (ดูบรรยายที่ 11 เพิ่มเติม)

การทดลองเกี่ยวกับการศึกษาการแข่งขันของ G. Gause เป็นที่รู้จักอย่างกว้างขวาง ซึ่งแสดงให้เห็นถึงความอยู่รอดของหนึ่งในสายพันธุ์ที่แข่งขันกัน และทำให้เขาสามารถกำหนด "กฎของการกีดกันทางการแข่งขัน" ได้ กฎหมายระบุว่ามีเพียงสายพันธุ์เดียวเท่านั้นที่สามารถดำรงอยู่ในช่องนิเวศน์เดียวได้ ในรูป 9.3. ผลลัพธ์ของการทดลองของ Gause ถูกนำเสนอสำหรับ Parametium สองสายพันธุ์ ซึ่งครอบครองช่องทางนิเวศน์เดียวกัน (รูปที่ 9.3 a, b) และสปีชีส์ที่อยู่ในนิเวศนิเวศที่แตกต่างกัน (รูปที่ 9.3 c)

ข้าว. 9.3. ก- กราฟการเติบโตของประชากรสองสายพันธุ์พาราเมเทียม ในพืชชนิดเดียว วงกลมสีดำ –พี.ออเรเลีย วงกลมสีขาว – พี. หาง

ข- กราฟการเจริญเติบโตของ P Aurelia และ P . หาง ในวัฒนธรรมผสมผสาน

โดย กอส, 1934

รูปแบบการแข่งขัน (9.2) มีข้อเสีย โดยเฉพาะอย่างยิ่งตามมาว่าการอยู่ร่วมกันของสองสายพันธุ์เป็นไปได้ก็ต่อเมื่อจำนวนของพวกเขาถูกจำกัดด้วยปัจจัยที่ต่างกัน แต่แบบจำลองไม่ได้ระบุว่าความแตกต่างจะต้องมากเพียงใดเพื่อให้แน่ใจว่าอยู่ร่วมกันในระยะยาว . ในเวลาเดียวกัน เป็นที่ทราบกันดีว่าสำหรับการอยู่ร่วมกันในระยะยาวในสภาพแวดล้อมที่เปลี่ยนแปลงไป ความแตกต่างถึงระดับหนึ่งเป็นสิ่งจำเป็น การแนะนำองค์ประกอบสุ่มเข้าไปในโมเดล (เช่น การแนะนำฟังก์ชันการใช้ทรัพยากร) ช่วยให้เราสามารถตรวจสอบปัญหาเหล่านี้ได้ในเชิงปริมาณ

ระบบนักล่า+เหยื่อ

(9.7)

ที่นี่ตรงกันข้ามกับ (9.2) สัญญาณ ข 12 และ ข 21 แตกต่างกัน เช่นเดียวกับในกรณีของการแข่งขันที่มา

(9.8)

เป็นจุดพิเศษประเภทโหนดที่ไม่เสถียร สถานะคงตัวที่เป็นไปได้อีกสามสถานะ:

,(9.9)

(9.10)

(9.11)

ดังนั้นจึงเป็นไปได้ที่เหยื่อเท่านั้นที่จะอยู่รอด (9.10) เฉพาะผู้ล่า (9.9) (หากมีแหล่งอาหารอื่น) และการอยู่ร่วมกันของทั้งสองสายพันธุ์ (9.11) เราได้กล่าวถึงตัวเลือกสุดท้ายในการบรรยายที่ 5 แล้ว ประเภทที่เป็นไปได้ของการถ่ายภาพบุคคลสำหรับระบบล่าเหยื่อจะแสดงไว้ในรูปที่ 1 9.4.

ไอโซลินของแทนเจนต์แนวนอนเป็นเส้นตรง

x 2 = – ข 21 เอ็กซ์ 1 /ค 2 + ก 1/ค2, เอ็กซ์ 2 = 0,

และไอโซไลน์ของแทนเจนต์แนวตั้ง- ตรง

x 2 = – ค 1 เอ็กซ์ 1 /ข 12 + ก 2 /ข 12 , เอ็กซ์ 1 = 0.

จุดที่อยู่นิ่งอยู่ที่จุดตัดของไอโซไลน์แทนเจนต์แนวตั้งและแนวนอน

จากรูป 9.4 ต่อไปนี้จะมองเห็นได้ ระบบล่าเหยื่อ (9.7) สามารถมีตำแหน่งสมดุลที่มั่นคงได้ซึ่งในโอ ประชากรเหล้ารัมของเหยื่อเสียชีวิตโดยสิ้นเชิง ( ) และเหลือเพียงผู้ล่าเท่านั้น (ช่วง 2 ในรูป 9.4 ก) แน่นอนว่าสถานการณ์ดังกล่าวสามารถเกิดขึ้นได้ก็ต่อเมื่อ นอกเหนือจากประเภทของเหยื่อที่เป็นปัญหาแล้ว เอ็กซ์นักล่า 1 คน เอ็กซ์ 2 – มีแหล่งพลังงานเพิ่มเติม ข้อเท็จจริงนี้สะท้อนให้เห็นในแบบจำลองด้วยเทอมบวกทางด้านขวาของสมการสำหรับ x2 จุดพิเศษ(1) และ (3) (รูปที่ 9.4 ก) ไม่เสถียร ความเป็นไปได้ที่สอง – สภาวะคงที่ซึ่งประชากรผู้ล่าตายหมดและเหลือเพียงเหยื่อเท่านั้น – จุดที่มั่นคง(3) (รูปที่ 9.4 6 ). นี่เป็นจุดพิเศษ (1) – ยังเป็นโหนดที่ไม่เสถียรอีกด้วย

ในที่สุดความเป็นไปได้ที่สาม – การอยู่ร่วมกันอย่างยั่งยืนของประชากรผู้ล่าและเหยื่อ (รูปที่. 9.4 วี) ตัวเลขคงที่ซึ่งแสดงโดยสูตร (9.11).

เช่นเดียวกับในกรณีของประชากรกลุ่มหนึ่ง (ดูการบรรยายที่ 3) สำหรับแบบจำลอง (9.7) เป็นไปได้ที่จะพัฒนาแบบจำลองสุ่ม แต่ไม่สามารถแก้ไขได้อย่างชัดเจน ดังนั้นเราจะจำกัดตัวเองอยู่เพียงการพิจารณาทั่วไปเท่านั้น ตัวอย่างเช่น สมมติว่าจุดสมดุลอยู่ห่างจากแต่ละแกน จากนั้นสำหรับวิถีเฟสที่มีค่าx 1 , x 2 ยังคงมีขนาดใหญ่เพียงพอ โมเดลเชิงกำหนดจะค่อนข้างน่าพอใจ แต่หาก ณ จุดใดจุดหนึ่งในวิถีเฟส ตัวแปรใดๆ ที่มีขนาดไม่ใหญ่มาก ความผันผวนแบบสุ่มก็อาจมีนัยสำคัญ พวกเขานำไปสู่ความจริงที่ว่าจุดตัวแทนเคลื่อนไปที่แกนใดแกนหนึ่งซึ่งหมายถึงการสูญพันธุ์ของสายพันธุ์ที่เกี่ยวข้อง

ดังนั้นแบบจำลองสุ่มจึงไม่เสถียรเนื่องจากการสุ่ม "ดริฟท์" ไม่ช้าก็เร็วจะนำไปสู่การสูญพันธุ์ของสายพันธุ์หนึ่ง ในรูปแบบนี้ ผู้ล่าจะสูญพันธุ์ในที่สุด ไม่ว่าจะโดยบังเอิญหรือเพราะประชากรเหยื่อถูกกำจัดก่อน แบบจำลองสุ่มของระบบนักล่า-เหยื่อ อธิบายการทดลองของเกาส์ได้ดี (Gause 1934), ซึ่งใน ciliates พาราเมตตัม แคนดาทัมทำหน้าที่เป็นเหยื่อของ ciliate อีกคน ดิดิเนียม นาซาทัม – นักล่า คาดหวังตามสมการที่กำหนด (9.7) ตัวเลขสมดุลในการทดลองเหล่านี้มีเพียงประมาณห้าตัวในแต่ละสปีชีส์ ดังนั้น จึงไม่น่าแปลกใจที่ในการทดลองซ้ำแต่ละครั้งทั้งผู้ล่าหรือเหยื่อ (และหลังจากนั้น ผู้ล่า) จะตายอย่างรวดเร็วมาก ผลลัพธ์ของการทดลองจะถูกนำเสนอ ในรูป 9.5.

ข้าว. 9.5. ความสูง พาราเมเทียม คอดาตัม และ ciliates ผู้ล่า ดาดิเนียมนาซูทัม. จาก : เกาส จี.เอฟ. การต่อสู้เพื่อการดำรงอยู่. บัลติมอร์, 1934

ดังนั้น การวิเคราะห์แบบจำลองปฏิสัมพันธ์ของสายพันธุ์ Volterra แสดงให้เห็นว่า แม้ว่าระบบดังกล่าวจะมีพฤติกรรมหลากหลายประเภท แต่ก็ไม่สามารถมีความผันผวนของจำนวนในแบบจำลองของสายพันธุ์ที่แข่งขันกันได้เลย อย่างไรก็ตาม การแกว่งดังกล่าวสังเกตได้จากธรรมชาติและในการทดลอง ความจำเป็นในการอธิบายทางทฤษฎีเป็นหนึ่งในเหตุผลในการกำหนดคำอธิบายแบบจำลองในรูปแบบทั่วไป

โมเดลปฏิสัมพันธ์ทั่วไปของสองประเภท

มีการเสนอแบบจำลองจำนวนมากเพื่ออธิบายปฏิสัมพันธ์ของสปีชีส์ โดยทางด้านขวามือของสมการนั้นเป็นฟังก์ชันของจำนวนประชากรที่มีปฏิสัมพันธ์กัน ประเด็นการพัฒนาเกณฑ์ทั่วไปเพื่อกำหนดประเภทของฟังก์ชันที่สามารถอธิบายพฤติกรรมของขนาดประชากรชั่วคราว รวมถึงความผันผวนที่คงที่ ได้รับการแก้ไขแล้ว โมเดลที่มีชื่อเสียงที่สุดเหล่านี้เป็นของ Kolmogorov (1935, บทความแก้ไข - 1972) และ Rosenzweig (1963)

(9.12)

แบบจำลองประกอบด้วยสมมติฐานดังต่อไปนี้:

1) ผู้ล่าไม่มีปฏิสัมพันธ์ซึ่งกันและกัน เช่น อัตราการสืบพันธุ์ของนักล่า เค 2 และจำนวนผู้ประสบภัย ลการกำจัดต่อหน่วยเวลาโดยผู้ล่าหนึ่งคนไม่ได้ขึ้นอยู่กับ ย.

2) การเพิ่มจำนวนเหยื่อต่อหน้าผู้ล่าเท่ากับการเพิ่มในกรณีที่ไม่มีผู้ล่าลบด้วยจำนวนเหยื่อที่ผู้ล่าทำลายล้าง ฟังก์ชั่น เค 1 (x), เค 2 (x), ล(x) มีความต่อเนื่องและกำหนดไว้บนครึ่งแกนบวก x, ย³ 0.

3) ดีเค 1 /dx< 0. ซึ่งหมายความว่าอัตราการสืบพันธุ์ของเหยื่อในกรณีที่ไม่มีผู้ล่าจะลดลงอย่างซ้ำซากจำเจเมื่อจำนวนเหยื่อเพิ่มขึ้น ซึ่งสะท้อนถึงความพร้อมของอาหารและทรัพยากรอื่นๆ ที่จำกัด

4) ดีเค 2 /dx> 0, เค 2 (0) < 0 < k 2 (¥ ). เมื่อจำนวนเหยื่อเพิ่มขึ้น ค่าสัมประสิทธิ์การแพร่พันธุ์ของสัตว์นักล่าจะลดลงอย่างซ้ำซากจำเจเมื่อจำนวนเหยื่อเพิ่มขึ้น โดยย้ายจากค่าลบ (เมื่อไม่มีอะไรจะกิน) ไปเป็นค่าบวก

5) จำนวนเหยื่อที่ถูกทำลายโดยผู้ล่าหนึ่งคนต่อหน่วยเวลา ล(x)> 0 ที่ ญ> 0; ล(0)=0.

ประเภทที่เป็นไปได้ของภาพบุคคลของระบบ (9.12) แสดงไว้ในรูปที่ 1 9.6:

ข้าว. 9.6.ภาพบุคคลเฟสของระบบโคลโมโกรอฟ (9.12) ซึ่งอธิบายปฏิสัมพันธ์ของสองประเภทที่อัตราส่วนของพารามิเตอร์ที่แตกต่างกัน คำอธิบายในข้อความ

โซลูชันแบบคงที่ (มีสองหรือสาม) มีพิกัดต่อไปนี้:

(1). ` x=0;` ย=0.

ที่มาของพิกัดสำหรับค่าพารามิเตอร์ใด ๆ คืออาน (รูปที่ 9.6 a-d)

(2). ` x=ก,` ย=0.(9.13)

กกำหนดจากสมการ:

เค 1 (ก)=0.

เครื่องเขียน สารละลาย (9.13) ถือเป็นอานถ้า บี< ก (รูปที่ 9.6 ก, ข, ช), บี กำหนดจากสมการ

เค 2 (บี)=0

จุด (9.13) อยู่ในควอแดรนต์บวก ถ้า บี>ก . นี่คือโหนดที่เสถียร .

กรณีสุดท้ายซึ่งสอดคล้องกับการตายของผู้ล่าและความอยู่รอดของเหยื่อจะแสดงในรูปที่ 1 9.6 วี.

(3). ` x=ข,` ย=ค.(9.14)

ค่าของ C ถูกกำหนดจากสมการ:

จุด (9.14) – โฟกัส (รูปที่ 9.6 ก) หรือโหนด (รูปที่ 9.6 ช) ความเสถียรซึ่งขึ้นอยู่กับสัญญาณของปริมาณส

ส 2 = – เค 1 (ข) – ก 1 (บี)บี+แอล(บี)ค.

ถ้า ส>0, จุดจะมีเสถียรภาพถ้าส<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 ข)

ในวรรณคดีต่างประเทศ แบบจำลองที่คล้ายกันที่เสนอโดย Rosenzweig และ MacArthur (1963) มักถูกพิจารณามากกว่า:

(9.15)

ที่ไหน ฉ(x) - อัตราการเปลี่ยนแปลงจำนวนเหยื่อ xในกรณีที่ไม่มีผู้ล่า F( เอ็กซ์, ย) - ความรุนแรงของการปล้นสะดม เค- ค่าสัมประสิทธิ์ที่แสดงลักษณะของประสิทธิภาพของการประมวลผลชีวมวลเหยื่อให้เป็นชีวมวลนักล่า จ- การตายของนักล่า

โมเดล (9.15) ลดขนาดลงเป็นกรณีพิเศษของโมเดล Kolmogorov (9.12) ภายใต้สมมติฐานต่อไปนี้:

1) จำนวนผู้ล่าถูกจำกัดด้วยจำนวนเหยื่อเท่านั้น

2) ความเร็วที่ผู้ล่ากินเหยื่อนั้นขึ้นอยู่กับความหนาแน่นของประชากรเหยื่อเท่านั้น และไม่ขึ้นอยู่กับความหนาแน่นของประชากรนักล่า

จากนั้นสมการ (9.15) จะอยู่ในรูปแบบ

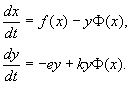
เมื่ออธิบายปฏิสัมพันธ์ของสิ่งมีชีวิตจริง ทางด้านขวามือของสมการจะถูกระบุตามแนวคิดเกี่ยวกับความเป็นจริงทางชีววิทยา ลองพิจารณาหนึ่งในโมเดลยอดนิยมประเภทนี้

แบบจำลองปฏิสัมพันธ์ระหว่างแมลง 2 ชนิด (แมคอาเธอร์, 1971)

แบบจำลองที่เราจะพิจารณาด้านล่างนี้ใช้เพื่อแก้ปัญหาในทางปฏิบัติในการควบคุมแมลงที่เป็นอันตรายโดยการฆ่าเชื้อตัวผู้ของสายพันธุ์ใดสายพันธุ์หนึ่ง จากลักษณะทางชีววิทยาของปฏิสัมพันธ์ของสปีชีส์ มีการเขียนแบบจำลองต่อไปนี้

(9.16)

ที่นี่ เอ็กซ์, ย- ชีวมวลของแมลง 2 ชนิด ปฏิสัมพันธ์ทางโภชนาการของสายพันธุ์ที่อธิบายไว้ในแบบจำลองนี้มีความซับซ้อนมาก สิ่งนี้จะกำหนดรูปแบบของพหุนามทางด้านขวามือของสมการ

ลองดูทางด้านขวาของสมการแรก แมลงชนิดต่างๆ เอ็กซ์กินตัวอ่อนของสายพันธุ์ ที่(สมาชิก +เค 3 ใช่)แต่ผู้ใหญ่ของสายพันธุ์ ที่กินตัวอ่อนของสายพันธุ์ เอ็กซ์ขึ้นอยู่กับความอุดมสมบูรณ์ของสายพันธุ์สูง เอ็กซ์หรือ ที่หรือทั้งสองประเภท (สมาชิก –เค 4 xy, – y 2). ตอนเล็กๆ เอ็กซ์การตายของสายพันธุ์ เอ็กซ์สูงกว่าการเพิ่มขึ้นตามธรรมชาติ (1 –เค 1 +เค 2 x–x2 < 0 มีขนาดเล็ก เอ็กซ์)ในสมการที่สองคือเทอม เค 5 สะท้อนถึงการเจริญเติบโตตามธรรมชาติของสายพันธุ์ ใช่; –เค 6 คุณ –การยับยั้งชั่งใจตนเองประเภทนี้–เค 7 x– กินตัวอ่อนของสายพันธุ์ ที่แมลงชนิด เอ็กซ์ เค 8 เอ็กซ์ซี – การเพิ่มขึ้นของมวลชีวมวลชนิด ที่เนื่องจากการบริโภคของแมลงที่โตเต็มวัยในสายพันธุ์ ที่ตัวอ่อนของสายพันธุ์ เอ็กซ์

ในรูป 9.7 วงจรจำกัดจะแสดงขึ้น ซึ่งเป็นวิถีของการแก้ปัญหาของระบบเป็นระยะที่เสถียร (9.16).

วิธีแก้ปัญหาสำหรับคำถามว่าจะประกันการอยู่ร่วมกันของประชากรกับสภาพแวดล้อมทางชีวภาพได้อย่างไรนั้นแน่นอนว่าไม่สามารถหาได้โดยไม่คำนึงถึงลักษณะเฉพาะของระบบทางชีววิทยาเฉพาะและการวิเคราะห์ความสัมพันธ์ทั้งหมดของระบบ ในเวลาเดียวกัน การศึกษาแบบจำลองทางคณิตศาสตร์อย่างเป็นทางการช่วยให้เราสามารถตอบคำถามทั่วไปบางข้อได้ อาจเป็นที่ถกเถียงกันอยู่ว่าสำหรับแบบจำลองเช่น (9.12) ข้อเท็จจริงของความเข้ากันได้หรือความไม่ลงรอยกันของประชากรไม่ได้ขึ้นอยู่กับขนาดเริ่มต้น แต่จะถูกกำหนดโดยธรรมชาติของปฏิสัมพันธ์ของสายพันธุ์เท่านั้น แบบจำลองนี้ช่วยตอบคำถาม: ทำอย่างไรจึงจะมีอิทธิพลต่อ biocenosis และจัดการมันเพื่อทำลายสายพันธุ์ที่เป็นอันตรายอย่างรวดเร็ว

การจัดการอาจลดลงเหลือเพียงการเปลี่ยนแปลงค่าประชากรอย่างกะทันหันในระยะสั้น เอ็กซ์และ ยู.วิธีนี้สอดคล้องกับวิธีการควบคุม เช่น การทำลายประชากรกลุ่มหนึ่งหรือทั้งสองกลุ่มเพียงครั้งเดียวหรือทั้งสองกลุ่มด้วยวิธีทางเคมี จากข้อความที่ร่างไว้ข้างต้น เป็นที่ชัดเจนว่าสำหรับประชากรที่เข้ากันได้ วิธีการควบคุมนี้จะไม่ได้ผล เนื่องจากเมื่อเวลาผ่านไป ระบบจะเข้าสู่ระบอบการปกครองแบบคงที่อีกครั้ง

อีกวิธีหนึ่งคือการเปลี่ยนประเภทของฟังก์ชันการโต้ตอบระหว่างมุมมอง เช่น เมื่อเปลี่ยนค่าของพารามิเตอร์ระบบ เป็นวิธีการแบบพาราเมตริกที่วิธีการควบคุมทางชีวภาพสอดคล้องกัน ดังนั้นเมื่อมีการนำไก่ตัวผู้ที่ทำหมัน อัตราการเติบโตของประชากรตามธรรมชาติจึงลดลง หากในเวลาเดียวกันเราได้ภาพเฟสประเภทอื่น ซึ่งมีเพียงสถานะคงที่คงที่โดยไม่มีจำนวนศัตรูพืชเป็นศูนย์ การควบคุมจะนำไปสู่ผลลัพธ์ที่ต้องการ – การทำลายประชากรของสายพันธุ์ที่เป็นอันตราย เป็นที่น่าสนใจที่จะทราบว่าบางครั้งขอแนะนำให้ใช้ผลกระทบไม่ใช่กับศัตรูพืชโดยตรง แต่กับคู่ของมันด้วย โดยทั่วไปเป็นไปไม่ได้ที่จะบอกว่าวิธีใดมีประสิทธิภาพมากกว่า ขึ้นอยู่กับการควบคุมที่มีอยู่และรูปแบบที่ชัดเจนของฟังก์ชันที่อธิบายปฏิสัมพันธ์ของประชากร

นางแบบโดย A.D. Bazykin

การวิเคราะห์ทางทฤษฎีของแบบจำลองปฏิสัมพันธ์ของสปีชีส์ได้รับการดำเนินการอย่างครอบคลุมที่สุดในหนังสือของ A.D. Bazykin เรื่อง “ชีวฟิสิกส์ของการโต้ตอบของประชากร” (M., Nauka, 1985)

ลองพิจารณาแบบจำลองนักล่าและเหยื่อตัวหนึ่งที่ศึกษาในหนังสือเล่มนี้

(9.17)

ระบบ (9.17) เป็นภาพรวมของแบบจำลองนักล่า-เหยื่อของโวลเทอร์ราที่ง่ายที่สุด (5.17) โดยคำนึงถึงผลกระทบของความอิ่มตัวของนักล่า แบบจำลอง (5.17) ถือว่าความเข้มของการแทะเล็มเหยื่อเพิ่มขึ้นเป็นเส้นตรงกับความหนาแน่นของเหยื่อที่เพิ่มขึ้น ซึ่งไม่สอดคล้องกับความเป็นจริงที่ความหนาแน่นของเหยื่อสูง สามารถเลือกฟังก์ชันต่างๆ เพื่ออธิบายการพึ่งพาอาหารของผู้ล่าต่อความหนาแน่นของเหยื่อได้ สิ่งสำคัญที่สุดคือการเลือกฟังก์ชั่นที่มีการเติบโต xมีแนวโน้มเชิงเส้นกำกับเป็นค่าคงที่ โมเดล (9.6) ใช้การพึ่งพาลอจิสติกส์ ในแบบจำลองของ Bazykin ไฮเปอร์โบลาจะถูกเลือกเป็นฟังก์ชันดังกล่าว x/(1+พิกเซล). โปรดจำไว้ว่านี่คือรูปแบบของสูตร Monod ซึ่งอธิบายการพึ่งพาอัตราการเติบโตของจุลินทรีย์กับความเข้มข้นของสารตั้งต้น ที่นี่เหยื่อมีบทบาทเป็นสารตั้งต้นและผู้ล่ามีบทบาทเป็นจุลินทรีย์ .

ระบบ (9.17) ขึ้นอยู่กับพารามิเตอร์เจ็ดตัว จำนวนพารามิเตอร์สามารถลดลงได้โดยการแทนที่ตัวแปร:

x® (เอ/ดี)เอ็กซ์; ย ® (เอ/ดี)/ป;

ที® (1/ก)เสื้อ; ก. (9.18)

และขึ้นอยู่กับพารามิเตอร์สี่ตัว

สำหรับการศึกษาเชิงคุณภาพที่สมบูรณ์ จำเป็นต้องแบ่งพื้นที่พารามิเตอร์สี่มิติออกเป็นส่วนที่มีพฤติกรรมไดนามิกประเภทต่างๆ เช่น สร้างภาพพาราเมตริกหรือโครงสร้างของระบบ

จากนั้น จึงจำเป็นต้องสร้างภาพบุคคลในเฟสสำหรับแต่ละพื้นที่ของภาพบุคคลแบบพาราเมตริก และอธิบายการแยกไปสองทางที่เกิดขึ้นกับภาพบุคคลในเฟสที่ขอบเขตของพื้นที่ต่างๆ ของภาพบุคคลแบบพาราเมตริก

การสร้างแนวตั้งพาราเมตริกที่สมบูรณ์นั้นดำเนินการในรูปแบบของชุด "ชิ้น" (การฉายภาพ) ของแนวตั้งพาราเมตริกมิติต่ำที่มีค่าคงที่ของพารามิเตอร์บางตัว

ภาพพาราเมตริกของระบบ (9.18) สำหรับการแก้ไข กและเล็ก จนำเสนอในรูปที่ 9.8 แนวตั้งประกอบด้วย 10 พื้นที่ซึ่งมีพฤติกรรมประเภทต่างๆ ของวิถีเฟส

ข้าว. 9.8.ภาพพาราเมตริกของระบบ (9.18) สำหรับการแก้ไขก

และเล็ก จ

พฤติกรรมของระบบที่อัตราส่วนพารามิเตอร์ต่างกันอาจแตกต่างกันอย่างมีนัยสำคัญ (รูปที่ 9.9) ระบบอนุญาตให้:

1) หนึ่งสมดุลที่มั่นคง (ภูมิภาค 1 และ 5)

2) หนึ่งรอบขีดจำกัดที่มั่นคง (ภูมิภาค 3 และ 8)

3) สองสมดุลที่มั่นคง (ภูมิภาค 2)

4) วงจรจำกัดที่เสถียรและความสมดุลภายในที่ไม่เสถียร (ภูมิภาค 6, 7, 9, 10)

5) วงจรจำกัดที่เสถียรและความสมดุลภายนอกที่เสถียร (ภูมิภาค 4)

ในบริเวณพาราเมตริก 7, 9, 10 บริเวณแรงดึงดูดของสมดุลถูกจำกัดด้วยวงจรขีดจำกัดที่ไม่เสถียรซึ่งอยู่ภายในวงจรที่เสถียร โครงสร้างที่น่าสนใจที่สุดคือเฟสแนวตั้ง ซึ่งสอดคล้องกับพื้นที่ 6 ในแนวตั้งพาราเมตริก จะแสดงโดยละเอียดในรูป. 9.10.

พื้นที่ดึงดูดสมดุล B 2 (แรเงา) คือ “หอยทาก” ที่บิดเบี้ยวจากโฟกัสที่ไม่เสถียร B 1 หากทราบว่าในช่วงเวลาเริ่มต้นระบบอยู่ในบริเวณใกล้เคียงกับ B 1 ก็เป็นไปได้ที่จะตัดสินว่าวิถีโคจรที่สอดคล้องกันจะไปถึงจุดสมดุล B 2 หรือวงจรจำกัดที่เสถียรรอบๆ จุดสมดุลสามจุด C (อาน) B 1 และ B 2 ขึ้นอยู่กับการพิจารณาความน่าจะเป็น

รูปที่ 9.10.ภาพเฟสของระบบ 9.18 สำหรับขอบเขตพาราเมตริก 6 ขอบเขตแรงดึงดูด B 2 ถูกแรเงา

ในแนวตั้งแบบพาราเมตริก(9.7) มี 22 ขอบเขตการแยกไปต่างๆ ที่เกิดขึ้น 7 การแยกไปสองทางประเภทต่างๆ การศึกษาของพวกเขาช่วยให้เราสามารถระบุประเภทของพฤติกรรมที่เป็นไปได้ของระบบเมื่อพารามิเตอร์เปลี่ยนแปลง เช่น เมื่อย้ายออกจากพื้นที่ 1 ถึงพื้นที่ 3 การกำเนิดของวงจรขีดจำกัดเล็กๆ เกิดขึ้น หรือการกำเนิดแบบนุ่มนวลของการแกว่งตัวของตัวเองรอบสมดุลเดียว ใน.การเกิดความผันผวนในตัวเองที่นุ่มนวลคล้ายกัน แต่อยู่รอบ ๆ ความสมดุลประการหนึ่งกล่าวคือ บี 1 , เกิดขึ้นเมื่อข้ามเขตแดน 2 และ 4. เมื่อออกจากพื้นที่ 4 ถึงพื้นที่ 5 วงรอบขีดจำกัดคงที่รอบจุดหนึ่งบี 1 “ระเบิด” บนวงของตัวแยกและจุดดึงดูดเพียงจุดเดียวที่ยังคงสมดุล บี 2 ฯลฯ

สิ่งที่น่าสนใจเป็นพิเศษสำหรับการปฏิบัติคือการพัฒนาเกณฑ์สำหรับความใกล้ชิดของระบบกับขอบเขตที่แยกไปสองทาง แท้จริงแล้ว นักชีววิทยาตระหนักดีถึงคุณสมบัติ "การบัฟเฟอร์" หรือ "ความยืดหยุ่น" ของระบบนิเวศทางธรรมชาติ คำเหล่านี้มักหมายถึงความสามารถของระบบในการดูดซับอิทธิพลภายนอก ตราบใดที่ความรุนแรงของอิทธิพลภายนอกไม่เกินค่าวิกฤติ พฤติกรรมของระบบจะไม่เกิดการเปลี่ยนแปลงเชิงคุณภาพ บนระนาบเฟสสิ่งนี้สอดคล้องกับการส่งคืนของระบบสู่สภาวะสมดุลที่เสถียรหรือวงจรลิมิตที่เสถียรซึ่งพารามิเตอร์ไม่แตกต่างจากเดิมมากนัก เมื่อความรุนแรงของการกระแทกเกินระดับที่อนุญาต ระบบจะ "พังทลาย" และเข้าสู่โหมดพฤติกรรมไดนามิกที่แตกต่างในเชิงคุณภาพ ตัวอย่างเช่น ระบบจะดับลง ปรากฏการณ์นี้สอดคล้องกับการเปลี่ยนแปลงแบบแยกไปสองทาง

การเปลี่ยนแปลงแยกไปสองประเภทแต่ละประเภทมีคุณสมบัติที่โดดเด่นของตัวเอง ซึ่งทำให้สามารถตัดสินอันตรายของการเปลี่ยนแปลงดังกล่าวในระบบนิเวศได้ ต่อไปนี้เป็นเกณฑ์ทั่วไปบางประการที่ระบุถึงความใกล้ชิดของชายแดนที่เป็นอันตราย เช่นเดียวกับในกรณีของสายพันธุ์หนึ่ง หากเมื่อจำนวนของสายพันธุ์หนึ่งลดลง ระบบ "ติด" ใกล้กับจุดอานที่ไม่เสถียร ซึ่งแสดงออกมาในการคืนตัวเลขกลับเป็นค่าเริ่มต้นอย่างช้ามาก จากนั้น ระบบอยู่ใกล้ขอบเขตวิกฤติ ตัวบ่งชี้อันตรายก็คือการเปลี่ยนแปลงรูปร่างของความผันผวนของจำนวนผู้ล่าและเหยื่อ หากการแกว่งที่ใกล้กับฮาร์มอนิกกลายเป็นการสั่น และแอมพลิจูดของการแกว่งเพิ่มขึ้น สิ่งนี้อาจทำให้ระบบสูญเสียเสถียรภาพและการสูญพันธุ์ของหนึ่งในสายพันธุ์

ทฤษฎีทางคณิตศาสตร์ที่ลึกซึ้งยิ่งขึ้นของการมีปฏิสัมพันธ์ระหว่างสปีชีส์นั้นเป็นไปตามรายละเอียดโครงสร้างของประชากรและคำนึงถึงปัจจัยทางโลกและอวกาศด้วย

วรรณกรรม.

โคลโมโกรอฟ เอ.เอ็น. การศึกษาเชิงคุณภาพแบบจำลองทางคณิตศาสตร์ของพลวัตประชากร // ปัญหาของไซเบอร์เนติกส์ ม., 1972, ฉบับที่ 5.

MacArtur R. การวิเคราะห์เชิงกราฟิกของระบบนิเวศ // แผนกชีววิทยารายงานมหาวิทยาลัย Perinceton 1971

A.D. Bazykin “ชีวฟิสิกส์ของการมีปฏิสัมพันธ์ของประชากร” ม. เนากา 2528

V. Volterra: “ทฤษฎีทางคณิตศาสตร์แห่งการต่อสู้เพื่อการดำรงอยู่” ม.. วิทยาศาสตร์ พ.ศ. 2519

กอส จี.เอฟ. การต่อสู้เพื่อการดำรงอยู่. บัลติมอร์ 2477