ฟังก์ชันเลขชี้กำลังลดลงภายใต้เงื่อนไขใด สมการเลขชี้กำลังและอสมการ
ฟังก์ชันเลขชี้กำลังและลอการิทึม VIII
§ 179 คุณสมบัติพื้นฐานของฟังก์ชันเลขชี้กำลัง
ในส่วนนี้เราจะศึกษาคุณสมบัติพื้นฐานของฟังก์ชันเลขชี้กำลัง
ย = ก x (1)
ให้เราจำไว้ว่าภายใต้ ก ในสูตร (1) เราหมายถึงจำนวนบวกคงที่ใดๆ ที่ไม่ใช่ 1
คุณสมบัติ 1. โดเมนของฟังก์ชันเลขชี้กำลังคือเซตของจำนวนจริงทั้งหมด
ในความเป็นจริงด้วยการบวก ก การแสดงออก ก x กำหนดไว้สำหรับจำนวนจริงใดๆ เอ็กซ์ .
คุณสมบัติ 2. ฟังก์ชันเลขชี้กำลังรับเฉพาะค่าบวกเท่านั้น
จริงๆ แล้วถ้า. เอ็กซ์ > 0 ดังนั้น ตามที่พิสูจน์แล้วในมาตรา 176
ก x > 0.
ถ้า เอ็กซ์ <. 0, то
ก x =
ที่ไหน - เอ็กซ์ มากกว่าศูนย์แล้ว นั่นเป็นเหตุผล เอ - x > 0 แต่แล้ว
ก x = > 0.
ในที่สุดเมื่อ เอ็กซ์ = 0
ก x = 1.
คุณสมบัติที่ 2 ของฟังก์ชันเลขชี้กำลังมีการตีความแบบกราฟิกอย่างง่าย ความจริงที่ว่ากราฟของฟังก์ชันนี้ (ดูรูปที่ 246 และ 247) ตั้งอยู่เหนือแกนแอบซิสซาทั้งหมด
คุณสมบัติ 3. ถ้า ก >1, แล้วเมื่อไหร่ เอ็กซ์ > 0 ก x > 1, และเมื่อใด เอ็กซ์ < 0 ก x < 1. ถ้า ก < 1, тโอ้ ตรงกันข้าม เมื่อไหร่ เอ็กซ์ > 0 ก x < 1, และเมื่อใด เอ็กซ์ < 0 ก x > 1.
คุณสมบัติของฟังก์ชันเอ็กซ์โปเนนเชียลนี้ยังทำให้สามารถตีความทางเรขาคณิตอย่างง่ายได้ ที่ ก > 1 (รูปที่ 246) เส้นโค้ง ย = ก x ซึ่งอยู่เหนือเส้นตรง ที่ = 1 ณ เอ็กซ์ > 0 และต่ำกว่าเส้นตรง ที่ = 1 ณ เอ็กซ์ < 0.
ถ้า ก < 1 (рис. 247), то, наоборот, кривые ย = ก x ซึ่งอยู่ใต้เส้นตรง ที่ = 1 ณ เอ็กซ์ > 0 และเหนือเส้นตรงนี้ที่ เอ็กซ์ < 0.
ให้เราแสดงหลักฐานอย่างเข้มงวดเกี่ยวกับคุณสมบัติที่ 3 อนุญาต ก > 1 และ เอ็กซ์ - จำนวนบวกตามอำเภอใจ มาแสดงกันเถอะ
ก x > 1.
ถ้าเป็นจำนวน เอ็กซ์ มีเหตุผล ( เอ็กซ์ = ม / n ) , ที่ ก x = ก ม./ n = n √ก ม .
เนื่องจาก ก > 1 แล้ว ก ม > 1 แต่รากของจำนวนที่มากกว่าหนึ่งย่อมมากกว่า 1 ด้วยเช่นกัน
ถ้า เอ็กซ์ เป็นจำนวนตรรกยะ แล้วจึงมีจำนวนตรรกยะบวก เอ็กซ์" และ เอ็กซ์" ซึ่งทำหน้าที่เป็นการประมาณทศนิยมของตัวเลข x :
เอ็กซ์"< х < х" .
แต่แล้ว โดยนิยามของดีกรีที่มีเลขชี้กำลังไม่ลงตัว
ก เอ็กซ์" < ก x < ก เอ็กซ์"" .
ดังที่แสดงไว้ข้างต้นเป็นจำนวน ก เอ็กซ์" มากกว่าหนึ่ง ดังนั้นจำนวน ก x , มากกว่า ก เอ็กซ์" จะต้องมากกว่า 1 ด้วย
เราจึงได้แสดงให้เห็นแล้วว่าเมื่อไร ก >1 และเป็นบวกโดยพลการ เอ็กซ์
ก x > 1.
ถ้าเป็นจำนวน เอ็กซ์ เป็นลบ เราก็จะได้
ก x =
หมายเลขอยู่ที่ไหน เอ็กซ์ คงจะเป็นบวกอยู่แล้ว นั่นเป็นเหตุผล เอ - x > 1. ดังนั้น
ก x = < 1.
ดังนั้นเมื่อ ก > 1 และค่าลบตามอำเภอใจ x
ก x < 1.
กรณีเมื่อ 0< ก < 1, легко сводится к уже рассмотренному случаю. Учащимся предлагается убедиться в этом самостоятельно.
คุณสมบัติ 4. ถ้า x = 0, แล้วโดยไม่คำนึงถึงก ก x =1.
สิ่งนี้ตามมาจากคำจำกัดความของระดับศูนย์ ค่ากำลังศูนย์ของจำนวนใดๆ ที่ไม่ใช่ศูนย์จะเท่ากับ 1 ในเชิงกราฟิก คุณสมบัตินี้แสดงตามข้อเท็จจริงที่ว่าสำหรับค่าใดๆ ก เส้นโค้ง ที่ = ก x (ดูรูปที่ 246 และ 247) ตัดแกน ที่ ณ จุดที่ 1
คุณสมบัติ 5. ที่ ก >1 ฟังก์ชันเลขชี้กำลัง = ก x กำลังเพิ่มขึ้นอย่างซ้ำซากจำเจ และสำหรับ < 1 - ลดลงอย่างน่าเบื่อ
คุณสมบัตินี้ยังช่วยให้สามารถตีความทางเรขาคณิตอย่างง่ายได้
ที่ ก > 1 (รูปที่ 246) เส้นโค้ง ที่ = ก x มีการเจริญเติบโต เอ็กซ์ สูงขึ้นเรื่อยๆ และเมื่อไร ก < 1 (рис. 247) - опускается все ниже и ниже.
ให้เราแสดงหลักฐานอย่างเข้มงวดเกี่ยวกับทรัพย์สินที่ 5
อนุญาต ก > 1 และ เอ็กซ์ 2 > เอ็กซ์ 1. มาแสดงกันเถอะ
ก x 2 > ก x 1
เนื่องจาก เอ็กซ์ 2 > เอ็กซ์ 1. จากนั้น เอ็กซ์ 2 = เอ็กซ์ 1 + ง , ที่ไหน ง - จำนวนบวกจำนวนหนึ่ง นั่นเป็นเหตุผล
ก x 2 - ก x 1 = ก x 1 + ง - ก x 1 = ก x 1 (ก ง - 1)
โดยคุณสมบัติที่ 2 ของฟังก์ชันเลขชี้กำลัง ก x 1 > 0 ตั้งแต่ ง > 0 จากนั้นตามด้วยคุณสมบัติที่ 3 ของฟังก์ชันเลขชี้กำลัง ก ง > 1. ปัจจัยทั้งสองในตัวผลิตภัณฑ์ ก x 1 (ก ง - 1) เป็นบวก ดังนั้นตัวผลิตภัณฑ์นี้เองจึงเป็นบวก วิธี, ก x 2 - ก x 1 > 0 หรือ ก x 2 > ก x 1 เป็นสิ่งที่ต้องพิสูจน์
แล้วเมื่อไหร่ล่ะ ก > 1 ฟังก์ชั่น ที่ = ก x กำลังเพิ่มขึ้นอย่างน่าเบื่อหน่าย ในทำนองเดียวกันก็พิสูจน์ได้ว่าเมื่อใด ก < 1 функция ที่ = ก x กำลังลดลงอย่างน่าเบื่อ
ผลที่ตามมา ถ้ากำลังสองของจำนวนบวกเดียวกันยกเว้น 1 เท่ากัน เลขชี้กำลังของพวกมันจะเท่ากัน
กล่าวอีกนัยหนึ่งถ้า
ก ข = ก ค (ก > 0 และ ก =/= 1),
ข = ค .
จริงๆแล้วถ้าเป็นตัวเลข ข และ กับ ไม่เท่ากัน เนื่องจากความซ้ำซากจำเจของฟังก์ชัน ที่ = ก x ยิ่งพวกเขายิ่งใหญ่เท่าไรก็ยิ่งสอดคล้องกับเท่านั้น ก มากกว่า 1 และเมื่อใด ก < 1 меньшее значение этой функции. Таким образом, было бы или ก ข > ก ค , หรือ ก ข < ก ค - ทั้งสองขัดแย้งกับเงื่อนไข ก ข = ก ค - ก็ยังคงต้องยอมรับว่า ข = ค .
คุณสมบัติ 6. ถ้าก > 1, แล้วมีการโต้แย้งเพิ่มขึ้นอย่างไม่จำกัด เอ็กซ์ (เอ็กซ์ -> ∞ ) ค่าฟังก์ชัน ที่ = ก x ยังเติบโตอย่างไม่มีกำหนด (ที่ -> ∞ ). เมื่อข้อโต้แย้งลดลงอย่างไม่มีขีดจำกัด เอ็กซ์ (เอ็กซ์ -> -∞ ) ค่าของฟังก์ชันนี้มีแนวโน้มที่จะเป็นศูนย์ในขณะที่ยังคงเป็นค่าบวก (ที่->0; ที่ > 0).
โดยคำนึงถึงความซ้ำซากจำเจของฟังก์ชันที่พิสูจน์แล้วข้างต้น ที่ = ก x เราสามารถพูดได้ว่าในกรณีที่กำลังพิจารณาฟังก์ชัน ที่ = ก x เพิ่มขึ้นอย่างน่าเบื่อจาก 0 เป็น ∞ .
ถ้า 0 <ก < 1, จากนั้นด้วยการเพิ่มขึ้นอย่างไม่ จำกัด ในอาร์กิวเมนต์ x (x -> ∞) ค่าของฟังก์ชัน y = a x มีแนวโน้มที่จะเป็นศูนย์ในขณะที่ยังคงเป็นบวก (ที่->0; ที่ > 0). เมื่ออาร์กิวเมนต์ x ลดลงอย่างไม่มีขีดจำกัด (เอ็กซ์ -> -∞ ) ค่าของฟังก์ชันนี้จะเพิ่มขึ้นอย่างไม่จำกัด (ที่ -> ∞ ).
เนื่องจากความซ้ำซากจำเจของฟังก์ชัน y = ก x เราสามารถพูดได้ว่าในกรณีนี้คือฟังก์ชัน ที่ = ก x ลดลงอย่างน่าเบื่อหน่ายจาก ∞ ถึง 0
คุณสมบัติที่ 6 ของฟังก์ชันเลขชี้กำลังสะท้อนให้เห็นอย่างชัดเจนในรูปที่ 246 และ 247 เราจะไม่พิสูจน์อย่างเคร่งครัด
สิ่งที่เราต้องทำคือสร้างช่วงของการแปรผันของฟังก์ชันเลขชี้กำลัง y = ก x (ก > 0, ก =/= 1).
ข้างต้นเราได้พิสูจน์ว่าฟังก์ชัน y = ก x รับเฉพาะค่าบวกและเพิ่มขึ้นอย่างซ้ำซากจำเจจาก 0 เป็น ∞ (ที่ ก > 1) หรือลดลงอย่างซ้ำซากจำเจจาก ∞ ถึง 0 (ที่ 0< ก <. 1). Однако остался невыясненным следующий вопрос: не претерпевает ли функция y = ก x มีการกระโดดเมื่อคุณเปลี่ยนหรือไม่? ต้องใช้ค่าบวกใดๆ หรือไม่? ปัญหานี้ได้รับการแก้ไขในเชิงบวก ถ้า ก > 0 และ ก =/= 1 แล้วจำนวนบวกจะเป็นเท่าใดก็ได้ ที่ 0 จะพบอย่างแน่นอน เอ็กซ์ 0 เช่นนั้น
ก x 0 = ที่ 0 .
(เนื่องจากความซ้ำซากจำเจของฟังก์ชัน y = ก x ค่าที่ระบุ เอ็กซ์ 0 จะเป็นคนเดียวเท่านั้น)
การพิสูจน์ข้อเท็จจริงนี้อยู่นอกเหนือขอบเขตของโครงการของเรา การตีความทางเรขาคณิตของมันคือค่าบวกใดๆ ที่ กราฟฟังก์ชัน 0 y = ก x จะตัดกันเป็นเส้นตรงอย่างแน่นอน ที่ = ที่ 0 และยิ่งกว่านั้น ณ จุดเดียวเท่านั้น (รูปที่ 248)
จากที่นี่คุณสามารถทำได้ เอาต์พุตถัดไปซึ่งเรากำหนดเป็นคุณสมบัติ 7
คุณสมบัติ 7. พื้นที่การเปลี่ยนแปลงของฟังก์ชันเลขชี้กำลัง y = a x (ก > 0, ก =/= 1)คือเซตของจำนวนบวกทั้งหมด
แบบฝึกหัด
1368 ค้นหาโดเมนของคำจำกัดความของฟังก์ชันต่อไปนี้:
1369 จำนวนใดต่อไปนี้มากกว่า 1 และจำนวนใดน้อยกว่า 1:
1370. ขึ้นอยู่กับคุณสมบัติของฟังก์ชันเอ็กซ์โพเนนเชียลที่สามารถระบุได้
ก) (5/7) 2.6 > (5/7) 2.5; ข) (4 / 3) 1.3 > (4 / 3) 1.2
1371 จำนวนใดมากกว่า:
ก) π - √3 หรือ (1/ π ) - √3 ; ค) (2/3) 1 + √6 หรือ (2 / 3) √2 + √5 ;
ข) ( π / 4) 1 + √3 หรือ ( π / 4) 2; ง) (√3) √2 - √5 หรือ (√3) √3 - 2 ?
1372. อสมการเทียบเท่ากันหรือไม่:
1373 สิ่งที่สามารถพูดเกี่ยวกับตัวเลขได้ เอ็กซ์ และ ที่ , ถ้า เอ็กซ์ = และคุณ , ที่ไหน ก - จำนวนบวกที่กำหนด?
1374 1) เป็นไปได้หรือไม่ในบรรดาค่าทั้งหมดของฟังก์ชัน ที่ = 2x เน้น:
2) เป็นไปได้ไหมในทุกค่าของฟังก์ชัน ที่ = 2 | x| เน้น:
ก) มูลค่าสูงสุด- b) ค่าที่น้อยที่สุด?
การแก้ปัญหาทางคณิตศาสตร์ส่วนใหญ่ไม่ทางใดก็ทางหนึ่งเกี่ยวข้องกับการเปลี่ยนนิพจน์ตัวเลข พีชคณิต หรือฟังก์ชัน ข้อความข้างต้นมีผลใช้กับการตัดสินใจโดยเฉพาะ ในเวอร์ชันของการสอบ Unified State ในวิชาคณิตศาสตร์ ปัญหาประเภทนี้จะรวมถึงงาน C3 โดยเฉพาะ การเรียนรู้ที่จะแก้ปัญหางาน C3 มีความสำคัญไม่เพียงแต่เพื่อความสำเร็จเท่านั้น ผ่านการสอบ Unified Stateแต่ด้วยเหตุผลที่ว่าทักษะนี้จะมีประโยชน์เมื่อเรียนวิชาคณิตศาสตร์ในโรงเรียนมัธยมปลายด้วย
เมื่อเสร็จสิ้นภารกิจ C3 คุณต้องตัดสินใจ ประเภทต่างๆสมการและอสมการ ในหมู่พวกเขามีเหตุผล, ไม่ลงตัว, เอ็กซ์โปเนนเชียล, ลอการิทึม, ตรีโกณมิติ, โมดูลที่มี (ค่าสัมบูรณ์) เช่นเดียวกับโมดูลที่รวมกัน บทความนี้จะกล่าวถึงสมการเอ็กซ์โพเนนเชียลและอสมการประเภทหลักๆ ตลอดจนวิธีการต่างๆ ในการแก้สมการเหล่านี้ อ่านเกี่ยวกับการแก้สมการและอสมการประเภทอื่นๆ ในส่วน "" ในบทความเกี่ยวกับวิธีแก้ไขปัญหา C3 จาก Unified State Examination ในวิชาคณิตศาสตร์
ก่อนที่เราจะเริ่มวิเคราะห์เจาะจง สมการเลขชี้กำลังและอสมการในฐานะครูสอนคณิตศาสตร์ ฉันขอแนะนำให้คุณทบทวนบางอย่าง วัสดุทางทฤษฎีซึ่งเราจะต้อง
ฟังก์ชันเลขชี้กำลัง
ฟังก์ชันเลขชี้กำลังคืออะไร?
หน้าที่ของแบบฟอร์ม ย = เอ็กซ์, ที่ไหน ก> 0 และ ก≠ 1 ถูกเรียก ฟังก์ชันเลขชี้กำลัง.
ขั้นพื้นฐาน คุณสมบัติของฟังก์ชันเลขชี้กำลัง ย = เอ็กซ์:
กราฟของฟังก์ชันเลขชี้กำลัง
กราฟของฟังก์ชันเลขชี้กำลังคือ เลขชี้กำลัง:
กราฟของฟังก์ชันเลขชี้กำลัง (เลขชี้กำลัง)
การแก้สมการเลขชี้กำลัง
บ่งชี้เรียกว่าสมการซึ่งตัวแปรที่ไม่รู้จักจะพบได้เฉพาะในเลขยกกำลังบางค่าเท่านั้น
เพื่อแก้ปัญหา สมการเลขชี้กำลังคุณต้องรู้และสามารถใช้ทฤษฎีบทง่ายๆ ต่อไปนี้ได้:
ทฤษฎีบท 1สมการเลขชี้กำลัง ก ฉ(x) = ก ก(x) (ที่ไหน ก > 0, ก≠ 1) เทียบเท่ากับสมการ ฉ(x) = ก(x).
นอกจากนี้ยังเป็นประโยชน์ในการจดจำสูตรพื้นฐานและการดำเนินการด้วยองศา:
Title="แสดงผลโดย QuickLaTeX.com">!}
ตัวอย่างที่ 1แก้สมการ:
สารละลาย:เราใช้สูตรและการทดแทนข้างต้น:
สมการจะกลายเป็น:
แยกแยะของที่ได้รับ สมการกำลังสองเชิงบวก:
Title="แสดงผลโดย QuickLaTeX.com">!}
ซึ่งหมายความว่าสมการนี้มีสองราก เราพบพวกเขา:
ไปสู่การทดแทนแบบย้อนกลับเราจะได้:
สมการที่สองไม่มีราก เนื่องจากฟังก์ชันเอ็กซ์โปเนนเชียลจะเป็นค่าบวกอย่างเคร่งครัดตลอดขอบเขตคำจำกัดความทั้งหมด มาแก้อันที่สองกัน:
เมื่อคำนึงถึงสิ่งที่กล่าวไว้ในทฤษฎีบทที่ 1 เราจะไปยังสมการที่เทียบเท่ากัน: x= 3 นี่จะเป็นคำตอบของงาน
คำตอบ: x = 3.
ตัวอย่างที่ 2แก้สมการ:
สารละลาย:สมการไม่มีข้อจำกัดเกี่ยวกับช่วงของค่าที่อนุญาต เนื่องจากนิพจน์รากนั้นเหมาะสมกับค่าใดๆ x(ฟังก์ชันเลขชี้กำลัง ย = 9 4 -xบวกและไม่เท่ากับศูนย์)
เราแก้สมการด้วยการแปลงที่เท่ากันโดยใช้กฎการคูณและการหารยกกำลัง:
การเปลี่ยนแปลงครั้งล่าสุดดำเนินการตามทฤษฎีบทที่ 1
คำตอบ:x= 6.
ตัวอย่างที่ 3แก้สมการ:
สารละลาย:ทั้งสองด้านของสมการดั้งเดิมสามารถหารด้วย 0.2 x- การเปลี่ยนแปลงนี้จะเท่ากัน เนื่องจากนิพจน์นี้มีค่ามากกว่าศูนย์สำหรับค่าใดๆ x(ฟังก์ชันเลขชี้กำลังเป็นบวกอย่างเคร่งครัดในโดเมนของคำจำกัดความ) จากนั้นสมการจะอยู่ในรูปแบบ:
คำตอบ: x = 0.
ตัวอย่างที่ 4แก้สมการ:
สารละลาย:เราลดความซับซ้อนของสมการให้เป็นสมการเบื้องต้นโดยใช้การแปลงที่เท่ากันโดยใช้กฎการหารและการคูณกำลังที่ให้ไว้ตอนต้นของบทความ:
หารทั้งสองข้างของสมการด้วย 4 xดังเช่นในตัวอย่างก่อนหน้านี้ เป็นการแปลงที่เทียบเท่า เนื่องจากนิพจน์นี้ไม่เท่ากับศูนย์สำหรับค่าใดๆ x.
คำตอบ: x = 0.
ตัวอย่างที่ 5แก้สมการ:
สารละลาย:การทำงาน ย = 3xยืนอยู่ทางด้านซ้ายของสมการกำลังเพิ่มขึ้น การทำงาน ย = —x-2/3 ทางด้านขวาของสมการกำลังลดลง ซึ่งหมายความว่าหากกราฟของฟังก์ชันเหล่านี้ตัดกัน จะมีจุดมากที่สุดเพียงจุดเดียว ในกรณีนี้ มันง่ายที่จะเดาว่ากราฟตัดกันที่จุดนั้น x= -1. จะไม่มีรากอื่น
คำตอบ: x = -1.
ตัวอย่างที่ 6แก้สมการ:
สารละลาย:เราทำให้สมการง่ายขึ้นด้วยการแปลงที่เท่ากัน โดยคำนึงถึงทุกที่ว่าฟังก์ชันเลขชี้กำลังมีค่ามากกว่าศูนย์สำหรับค่าใดๆ อย่างเคร่งครัด xและใช้กฎในการคำนวณผลคูณและผลหารของกำลังที่ให้ไว้ตอนต้นบทความ:
คำตอบ: x = 2.
การแก้อสมการเอ็กซ์โปเนนเชียล
บ่งชี้เรียกว่าอสมการซึ่งมีตัวแปรที่ไม่รู้จักอยู่ในเลขยกกำลังบางค่าเท่านั้น
เพื่อแก้ปัญหา อสมการเอ็กซ์โปเนนเชียลจำเป็นต้องมีความรู้เกี่ยวกับทฤษฎีบทต่อไปนี้:
ทฤษฎีบท 2ถ้า ก> 1 แล้วความไม่เท่าเทียมกัน ก ฉ(x) > ก ก(x) เทียบเท่ากับอสมการที่มีความหมายเดียวกัน: ฉ(x) > ก(x- ถ้า 0< ก < 1, то อสมการเอ็กซ์โปเนนเชียล ก ฉ(x) > ก ก(x) เทียบเท่ากับอสมการที่มีความหมายตรงกันข้าม: ฉ(x) < ก(x).
ตัวอย่างที่ 7แก้ความไม่เท่าเทียมกัน:
สารละลาย:ขอนำเสนอความไม่เท่าเทียมกันดั้งเดิมในรูปแบบ:
ลองหารทั้งสองข้างของอสมการนี้ด้วย 3 2 กัน xในกรณีนี้ (เนื่องจากผลบวกของฟังก์ชัน ย= 3 2x) เครื่องหมายอสมการจะไม่เปลี่ยนแปลง:
ลองใช้การทดแทน:
จากนั้นความไม่เท่าเทียมกันจะเกิดขึ้น:
ดังนั้น คำตอบของอสมการคือช่วง:
เมื่อย้ายไปที่การทดแทนแบบย้อนกลับเราจะได้:
เนื่องจากค่าบวกของฟังก์ชันเอ็กซ์โพเนนเชียล ความไม่เท่าเทียมกันทางด้านซ้ายจึงเป็นไปตามค่าอัตโนมัติ ด้วยการใช้คุณสมบัติที่รู้จักกันดีของลอการิทึม เราจึงมุ่งไปสู่อสมการที่เทียบเท่ากัน:
เนื่องจากฐานของระดับเป็นตัวเลขที่มากกว่า 1 เทียบเท่า (ตามทฤษฎีบท 2) จึงเป็นการเปลี่ยนไปสู่อสมการต่อไปนี้:
ในที่สุดเราก็ได้ คำตอบ:
ตัวอย่างที่ 8แก้ความไม่เท่าเทียมกัน:
สารละลาย:โดยใช้คุณสมบัติของการคูณและการหารยกกำลัง เราเขียนอสมการใหม่ในรูปแบบ:
ขอแนะนำตัวแปรใหม่:
เมื่อคำนึงถึงการทดแทนนี้ ความไม่เท่าเทียมกันจะอยู่ในรูปแบบ:
เมื่อคูณตัวเศษและส่วนของเศษส่วนด้วย 7 เราจะได้อสมการที่เทียบเท่ากันดังต่อไปนี้:
ดังนั้นค่าของตัวแปรต่อไปนี้จึงเป็นไปตามความไม่เท่าเทียมกัน ที:
จากนั้นเมื่อย้ายไปที่การทดแทนแบบย้อนกลับเราจะได้:
เนื่องจากฐานของระดับนี้มากกว่า 1 การเปลี่ยนไปสู่ความไม่เท่าเทียมกันจึงจะเท่ากัน (ตามทฤษฎีบท 2):
ในที่สุดเราก็ได้ คำตอบ:
ตัวอย่างที่ 9แก้ความไม่เท่าเทียมกัน:
สารละลาย:
เราแบ่งอสมการทั้งสองด้านด้วยนิพจน์:
ค่านี้จะมากกว่าศูนย์เสมอ (เนื่องจากฟังก์ชันเลขชี้กำลังเป็นบวก) ดังนั้นจึงไม่จำเป็นต้องเปลี่ยนเครื่องหมายอสมการ เราได้รับ:
t อยู่ในช่วง:
เมื่อพิจารณาถึงการทดแทนแบบย้อนกลับ เราพบว่าอสมการเดิมแบ่งออกเป็นสองกรณี:
อสมการประการแรกไม่มีทางแก้ได้เนื่องจากค่าบวกของฟังก์ชันเลขชี้กำลัง มาแก้อันที่สองกัน:
ตัวอย่างที่ 10แก้ความไม่เท่าเทียมกัน:
สารละลาย:
สาขาพาราโบลา ย = 2x+2-x 2 ชี้ลง ดังนั้นจึงถูกจำกัดจากด้านบนด้วยค่าที่มาถึงที่จุดยอด:
สาขาพาราโบลา ย = x 2 -2x+2 ในตัวบ่งชี้ชี้ขึ้นด้านบน ซึ่งหมายความว่ามันถูกจำกัดจากด้านล่างด้วยค่าที่มันไปถึงจุดยอด:
ในขณะเดียวกัน ฟังก์ชันก็ปรากฏว่ามีขอบเขตจากด้านล่างด้วย ย = 3 x 2 -2x+2 ซึ่งอยู่ทางด้านขวาของสมการ มันถึงค่าที่น้อยที่สุดที่จุดเดียวกับพาราโบลาในเลขชี้กำลัง และค่านี้คือ 3 1 = 3 ดังนั้น อสมการดั้งเดิมจะเป็นจริงได้ก็ต่อเมื่อฟังก์ชันทางด้านซ้ายและฟังก์ชันทางด้านขวาใช้ค่านั้น เท่ากับ 3 (จุดตัดของช่วงค่าของฟังก์ชันเหล่านี้คือตัวเลขนี้เท่านั้น) เงื่อนไขนี้จบที่จุดเดียว x = 1.
คำตอบ: x= 1.
เพื่อเรียนรู้ที่จะตัดสินใจ สมการเลขชี้กำลังและอสมการจำเป็นต้องฝึกฝนการแก้ปัญหาเหล่านี้อย่างต่อเนื่อง อุปกรณ์ช่วยสอนต่างๆ หนังสือปัญหาในคณิตศาสตร์ระดับประถมศึกษา ชุดปัญหาการแข่งขัน ชั้นเรียนคณิตศาสตร์ที่โรงเรียน รวมถึงบทเรียนตัวต่อตัวกับครูสอนพิเศษมืออาชีพสามารถช่วยคุณในงานที่ยากลำบากนี้ได้ ฉันขอให้คุณประสบความสำเร็จในการเตรียมตัวและผลการสอบที่ยอดเยี่ยม
เซอร์เกย์ วาเลรีวิช
ป.ล. เรียนแขกทุกท่าน! กรุณาอย่าเขียนคำขอเพื่อแก้สมการของคุณในความคิดเห็น น่าเสียดายที่ฉันไม่มีเวลาสำหรับเรื่องนี้เลย ข้อความดังกล่าวจะถูกลบ โปรดอ่านบทความ บางทีคุณอาจพบคำตอบสำหรับคำถามที่ไม่อนุญาตให้คุณแก้ไขงานด้วยตัวเองในนั้น
ก่อนอื่นให้เราแนะนำคำจำกัดความของฟังก์ชันเลขชี้กำลังก่อน
ฟังก์ชันเลขชี้กำลัง $f\left(x\right)=a^x$ โดยที่ $a >1$
ให้เราแนะนำคุณสมบัติของฟังก์ชันเลขชี้กำลังสำหรับ $a >1$
\ \[ไม่มีราก\] \
จุดตัดกับแกนพิกัด ฟังก์ชันจะไม่ตัดแกน $Ox$ แต่จะตัดแกน $Oy$ ที่จุด $(0,1)$
$f""\left(x\right)=(\left(a^xlna\right))"=a^x(ln)^2a$
\ \[ไม่มีราก\] \
กราฟ (รูปที่ 1)
รูปที่ 1 กราฟของฟังก์ชัน $f\left(x\right)=a^x,\ for\ a >1$
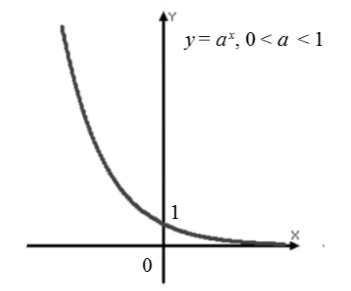
ฟังก์ชันเลขชี้กำลัง $f\left(x\right)=a^x$ โดยที่ $0
ให้เราแนะนำคุณสมบัติของฟังก์ชันเลขชี้กำลังที่ $0
โดเมนของคำจำกัดความคือจำนวนจริงทั้งหมด
$f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- ฟังก์ชันไม่เป็นคู่หรือคี่
$f(x)$ ต่อเนื่องตลอดโดเมนคำจำกัดความทั้งหมด
ช่วงของค่าคือช่วง $(0,+\infty)$
$f"(x)=\left(a^x\right)"=a^xlna$
\ \[ไม่มีราก\] \ \[ไม่มีราก\] \
ฟังก์ชันนี้นูนออกมาทั่วทั้งขอบเขตคำจำกัดความ
พฤติกรรมที่ส่วนท้ายของโดเมน:
\[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\]
กราฟ (รูปที่ 2)
ตัวอย่างปัญหาในการสร้างฟังก์ชันเลขชี้กำลัง
สำรวจและพลอตฟังก์ชัน $y=2^x+3$
สารละลาย.
เรามาศึกษาโดยใช้แผนภาพตัวอย่างด้านบน:
โดเมนของคำจำกัดความคือจำนวนจริงทั้งหมด
$f\left(-x\right)=2^(-x)+3$ -- ฟังก์ชันไม่เป็นคู่หรือคี่
$f(x)$ ต่อเนื่องตลอดโดเมนคำจำกัดความทั้งหมด
ช่วงของค่าคือช่วง $(3,+\infty)$
$f"\left(x\right)=(\left(2^x+3\right))"=2^xln2>0$
ฟังก์ชันนี้จะเพิ่มขึ้นทั่วทั้งขอบเขตคำจำกัดความ
$f(x)\ge 0$ ตลอดทั้งโดเมนของคำจำกัดความ
จุดตัดกับแกนพิกัด ฟังก์ชันไม่ตัดแกน $Ox$ แต่ตัดแกน $Oy$ ที่จุด ($0,4)$
$f""\left(x\right)=(\left(2^xln2\right))"=2^x(ln)^22>0$
ฟังก์ชันนี้นูนออกมาทั่วทั้งขอบเขตคำจำกัดความ
พฤติกรรมที่ส่วนท้ายของโดเมน:
\[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \อินฟินิตี้\]
กราฟ (รูปที่ 3)
รูปที่ 3 กราฟของฟังก์ชัน $f\left(x\right)=2^x+3$
ไฮเปอร์มาร์เก็ตแห่งความรู้ >>คณิตศาสตร์ >>คณิตศาสตร์ ชั้นประถมศึกษาปีที่ 10 >>
ฟังก์ชันเลขชี้กำลัง คุณสมบัติ และกราฟ
ลองพิจารณานิพจน์ 2x และค้นหาค่าของมันสำหรับค่าตรรกยะต่างๆ ของตัวแปร x เช่นสำหรับ x = 2;
โดยทั่วไป ไม่ว่าเราจะกำหนดความหมายเชิงตรรกยะให้กับตัวแปร x ก็ตาม เราก็สามารถคำนวณค่าตัวเลขที่สอดคล้องกันของนิพจน์ 2 x ได้เสมอ ดังนั้นเราจึงสามารถพูดคุยเกี่ยวกับเลขชี้กำลังได้ ฟังก์ชั่น y=2 x กำหนดบนเซต Q ของจำนวนตรรกยะ:
มาดูคุณสมบัติบางอย่างของฟังก์ชันนี้กัน
คุณสมบัติ 1.- ฟังก์ชั่นที่เพิ่มขึ้น เราดำเนินการพิสูจน์ในสองขั้นตอน
ขั้นแรก.ลองพิสูจน์ว่าถ้า r เป็นบวก จำนวนตรรกยะแล้ว 2 r >1
เป็นไปได้สองกรณี: 1) r - จำนวนธรรมชาติ, r = n; 2) ลดหย่อนสามัญไม่ได้ เศษส่วน,
ทางด้านซ้ายของอสมการสุดท้ายที่เรามี และทางด้านขวา 1 ซึ่งหมายความว่าสามารถเขียนอสมการสุดท้ายได้ในรูปแบบใหม่
ดังนั้น ไม่ว่าในกรณีใด อสมการ 2 r > 1 ยังคงอยู่ ซึ่งเป็นสิ่งที่จำเป็นต้องพิสูจน์
ขั้นตอนที่สองให้ x 1 และ x 2 เป็นตัวเลข และ x 1 และ x 2< х2. Составим разность 2 х2 -2 х1 и выполним некоторые ее преобразования:
(เราแทนความแตกต่าง x 2 - x 1 ด้วยตัวอักษร r)
เนื่องจาก r เป็นจำนวนตรรกยะบวก ดังนั้นสิ่งที่พิสูจน์แล้วในระยะแรก 2 r > 1 นั่นคือ 2 อาร์ -1 >0 จำนวน 2x" ก็เป็นค่าบวกเช่นกัน ซึ่งหมายความว่าผลคูณ 2 x-1 (2 Г -1) ก็เป็นค่าบวกเช่นกัน ดังนั้นเราจึงได้พิสูจน์แล้วว่า ความไม่เท่าเทียมกัน 2 Xg -2x">0
ดังนั้น จากอสมการ x 1< х 2 следует, что 2х" <2 x2 , а это и означает, что функция у -2х - возрастающая.
คุณสมบัติ 2.จำกัดจากด้านล่างและไม่จำกัดจากด้านบน
ขอบเขตของฟังก์ชันจากด้านล่างตามมาจากความไม่เท่าเทียมกัน 2 x >0 ซึ่งใช้ได้กับค่าใด ๆ ของ x จากโดเมนของคำจำกัดความของฟังก์ชัน ในเวลาเดียวกัน ไม่ว่าคุณจะหาจำนวนบวก M ใดก็ตาม คุณสามารถเลือกเลขยกกำลัง x ซึ่งจะทำให้อสมการ 2 x >M เป็นไปตามที่ต้องการ ซึ่งแสดงถึงความไม่มีขอบเขตของฟังก์ชันจากด้านบน ให้เรายกตัวอย่างจำนวนหนึ่ง
คุณสมบัติ 3.ไม่มีค่าที่เล็กที่สุดหรือใหญ่ที่สุด
อะไร ฟังก์ชั่นนี้ไม่มีนัยสำคัญใดยิ่งใหญ่ที่สุด เห็นได้ชัด เนื่องจากดังที่เราได้เห็นแล้วว่าไม่ได้จำกัดจากเบื้องบน แต่จำกัดจากด้านล่างทำไมไม่มีค่าขั้นต่ำ?
สมมติว่า 2 r เป็นค่าที่น้อยที่สุดของฟังก์ชัน (r คือค่าบางส่วน ตัวบ่งชี้ที่มีเหตุผล- ลองหาจำนวนตรรกยะ q กัน<г. Тогда в силу возрастания функции у=2 х будем иметь 2 x <2г. А это значит, что 2 r не может служить наименьшим значением функции.
คุณว่าทั้งหมดนี้เป็นสิ่งที่ดี แต่ทำไมเราถึงพิจารณาฟังก์ชัน y-2 x เฉพาะกับเซตของจำนวนตรรกยะ ทำไมเราไม่คิดว่ามันเหมือนกับฟังก์ชันอื่นๆ ที่รู้จักบนเส้นจำนวนทั้งหมด หรือในช่วงเวลาต่อเนื่องกันของ เส้นจำนวน? อะไรหยุดเรา? ลองคิดถึงสถานการณ์กัน
เส้นจำนวนไม่เพียงแต่ประกอบด้วยจำนวนตรรกยะเท่านั้น แต่ยังมีจำนวนอตรรกยะด้วย สำหรับฟังก์ชั่นที่ศึกษาก่อนหน้านี้สิ่งนี้ไม่ได้รบกวนเรา ตัวอย่างเช่น เราพบค่าของฟังก์ชัน y = x2 เท่าๆ กันอย่างง่ายดายสำหรับทั้งค่าตรรกยะและอตรรกยะของ x: ก็เพียงพอแล้วที่จะยกกำลังสองค่าที่กำหนดของ x
แต่ด้วยฟังก์ชัน y=2 x สถานการณ์จะซับซ้อนมากขึ้น หากอาร์กิวเมนต์ x ได้รับความหมายที่สมเหตุสมผลตามหลักการแล้ว x ก็สามารถคำนวณได้ (กลับไปที่จุดเริ่มต้นของย่อหน้าอีกครั้งซึ่งเราทำสิ่งนี้ทุกประการ) จะเกิดอะไรขึ้นถ้าอาร์กิวเมนต์ x ได้รับความหมายที่ไม่ลงตัว? เช่น จะคำนวณอย่างไร? เรายังไม่รู้เรื่องนี้
นักคณิตศาสตร์ได้ค้นพบทางออกแล้ว นั่นคือวิธีที่พวกเขาให้เหตุผล
เป็นที่ทราบกันว่า 
พิจารณาลำดับของจำนวนตรรกยะ - การประมาณทศนิยมของตัวเลขโดยข้อเสีย:
1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,732050; 1,7320508;... .
เป็นที่ชัดเจนว่า 1.732 = 1.7320 และ 1.732050 = 1.73205 เพื่อหลีกเลี่ยงการซ้ำซ้อน เราจะละทิ้งสมาชิกของลำดับที่ลงท้ายด้วยเลข 0
จากนั้นเราจะได้ลำดับที่เพิ่มขึ้น:
1; 1,7; 1,73; 1,732; 1,73205; 1,7320508;... .
ดังนั้นลำดับจึงเพิ่มขึ้น
เงื่อนไขทั้งหมดของลำดับนี้เป็นจำนวนบวกที่น้อยกว่า 22 กล่าวคือ ลำดับนี้มีจำกัด ตามทฤษฎีบทของไวเออร์ชตราส (ดูมาตรา 30) ถ้าลำดับเพิ่มขึ้นและมีขอบเขต ลำดับนั้นก็จะมาบรรจบกัน นอกจากนี้ จากมาตรา 30 เรารู้ว่าถ้าลำดับมาบรรจบกัน มันจะมาบรรจบกันเพียงขีดจำกัดเดียวเท่านั้น มีการตกลงกันว่าขีดจำกัดเดียวนี้ควรถือเป็นค่าของนิพจน์ตัวเลข และไม่สำคัญว่าจะหาค่าโดยประมาณของนิพจน์ตัวเลข 2 ได้ยากมาก สิ่งสำคัญคือนี่คือจำนวนเฉพาะ (ท้ายที่สุดเราไม่กลัวที่จะบอกว่ามันเป็นรากของสมการตรรกยะ 
รากของสมการตรีโกณมิติ โดยไม่ได้พิจารณาว่าตัวเลขเหล่านี้คืออะไร: 
ดังนั้นเราจึงได้ค้นพบความหมายของนักคณิตศาสตร์ที่ใส่ไว้ในสัญลักษณ์ 2^ ในทำนองเดียวกัน คุณสามารถระบุได้ว่า a คืออะไร และโดยทั่วไปแล้ว a คืออะไร โดยที่ a เป็นจำนวนอตรรกยะ และ a > 1
แต่ถ้าเป็น 0 ล่ะ<а <1? Как вычислить, например, ? Самым естественным способом: считать, что свести вычисления к случаю, когда основание степени больше 1.
ตอนนี้เราไม่เพียงแต่สามารถพูดคุยเรื่องกำลังที่มีเลขชี้กำลังตรรกศาสตร์ตามอำเภอใจเท่านั้น แต่ยังรวมถึงเรื่องกำลังที่มีเลขชี้กำลังจำนวนจริงตามอำเภอใจด้วย ได้รับการพิสูจน์แล้วว่าองศาที่มีเลขชี้กำลังจริงมีคุณสมบัติปกติทั้งหมดขององศา: เมื่อคูณยกกำลังด้วยฐานเดียวกัน เลขยกกำลังจะถูกบวก เมื่อหารจะถูกลบออก เมื่อเพิ่มระดับเป็นยกกำลังก็จะคูณ ฯลฯ แต่สิ่งที่สำคัญที่สุดคือตอนนี้เราสามารถพูดถึงฟังก์ชัน y-ax ที่กำหนดบนเซตของจำนวนจริงทั้งหมดได้แล้ว
ลองกลับไปที่ฟังก์ชัน y = 2 x และสร้างกราฟของมัน เมื่อต้องการทำเช่นนี้ เรามาสร้างตารางค่าฟังก์ชัน y=2x กัน:
มาทำเครื่องหมายจุดบนระนาบพิกัด (รูปที่ 194) โดยทำเครื่องหมายเส้นบางเส้นมาวาดกัน (รูปที่ 195)
คุณสมบัติของฟังก์ชัน y - 2 x:
1)
2) ไม่เป็นคู่หรือคี่; 248
3) เพิ่มขึ้น;
5) ไม่มีค่าที่ใหญ่ที่สุดหรือเล็กที่สุด
6) ต่อเนื่อง;
7)
8) นูนลง
การพิสูจน์อย่างเข้มงวดของคุณสมบัติที่ระบุไว้ของฟังก์ชัน y-2 x จะได้รับในวิชาคณิตศาสตร์ชั้นสูง เราได้กล่าวถึงคุณสมบัติเหล่านี้บางส่วนในระดับหนึ่งหรืออย่างอื่นก่อนหน้านี้ บางส่วนแสดงให้เห็นอย่างชัดเจนโดยกราฟที่สร้างขึ้น (ดูรูปที่ 195) ตัวอย่างเช่น การขาดความเท่าเทียมกันหรือความคี่ของฟังก์ชันมีความสัมพันธ์ทางเรขาคณิตกับการขาดความสมมาตรของกราฟ ตามลำดับ สัมพันธ์กับแกน y หรือสัมพันธ์กับจุดกำเนิด
ฟังก์ชันใดๆ ที่อยู่ในรูปแบบ y = a x โดยที่ a > 1 มีคุณสมบัติคล้ายกัน ในรูป 196 ในระบบพิกัดเดียวถูกสร้างขึ้น กราฟของฟังก์ชัน y=2 x, y=3 x, y=5 x
ตอนนี้เรามาพิจารณาฟังก์ชันและสร้างตารางค่าของมัน:
มาทำเครื่องหมายจุดบนระนาบพิกัด (รูปที่ 197) โดยทำเครื่องหมายเส้นบางเส้นมาวาดกัน (รูปที่ 198)
คุณสมบัติของฟังก์ชัน
1)
2) ไม่เป็นคู่หรือคี่;
3) ลดลง;
4) ไม่จำกัดจากด้านบน จำกัดจากด้านล่าง
5) ไม่มีค่าที่ใหญ่ที่สุดหรือน้อยที่สุด
6) ต่อเนื่อง;
7)
8) นูนลง
ฟังก์ชันใดๆ ที่อยู่ในรูป y = a x มีคุณสมบัติคล้ายกัน โดยที่ O<а <1. На рис. 200 в одной системе координат построены графики функций 
โปรดทราบ: กราฟฟังก์ชัน 
เหล่านั้น. y=2 x สมมาตรเกี่ยวกับแกน y (รูปที่ 201) นี่เป็นผลมาจากข้อความทั่วไป (ดูมาตรา 13): กราฟของฟังก์ชัน y = f(x) และ y = f(-x) มีความสมมาตรเกี่ยวกับแกน y ในทำนองเดียวกัน กราฟของฟังก์ชัน y = 3 x และ
เพื่อสรุปสิ่งที่กล่าวไว้ เราจะให้คำจำกัดความของฟังก์ชันเลขชี้กำลังและเน้นคุณสมบัติที่สำคัญที่สุดของฟังก์ชันนี้
คำนิยาม.ฟังก์ชันของแบบฟอร์มเรียกว่าฟังก์ชันเลขชี้กำลัง
คุณสมบัติพื้นฐานของฟังก์ชันเลขชี้กำลัง y = a x
กราฟของฟังก์ชัน y=a x สำหรับ a> 1 จะแสดงในรูป 201 และสำหรับ 0<а < 1 - на рис. 202.
เส้นโค้งที่แสดงในรูปที่. 201 หรือ 202 เรียกว่าเลขยกกำลัง ที่จริงแล้ว นักคณิตศาสตร์มักจะเรียกฟังก์ชันเอ็กซ์โปเนนเชียลว่า y = a x ดังนั้นคำว่า "เลขชี้กำลัง" จึงถูกใช้ในสองความหมาย คือ ทั้งเพื่อตั้งชื่อฟังก์ชันเลขชี้กำลัง และเพื่อตั้งชื่อกราฟของฟังก์ชันเลขชี้กำลัง โดยปกติแล้วความหมายจะชัดเจนว่าเรากำลังพูดถึงฟังก์ชันเลขชี้กำลังหรือกราฟของมัน
ให้ความสนใจกับคุณลักษณะทางเรขาคณิตของกราฟของฟังก์ชันเลขชี้กำลัง y=ax: แกน x คือเส้นกำกับแนวนอนของกราฟ จริงอยู่คำสั่งนี้มักจะชี้แจงดังนี้
แกน x คือเส้นกำกับแนวนอนของกราฟของฟังก์ชัน
กล่าวอีกนัยหนึ่ง
หมายเหตุสำคัญประการแรก เด็กนักเรียนมักสับสนคำศัพท์: ฟังก์ชันกำลัง, ฟังก์ชันเลขชี้กำลัง เปรียบเทียบ:
นี่คือตัวอย่างของฟังก์ชันกำลัง 
นี่คือตัวอย่างของฟังก์ชันเลขชี้กำลัง
โดยทั่วไป y = x r โดยที่ r เป็นตัวเลขเฉพาะ เป็นฟังก์ชันยกกำลัง (อาร์กิวเมนต์ x อยู่ในฐานของดีกรี)
y = a" โดยที่ a เป็นจำนวนเฉพาะ (บวกและแตกต่างจาก 1) เป็นฟังก์ชันเลขชี้กำลัง (อาร์กิวเมนต์ x อยู่ในเลขชี้กำลัง)
ฟังก์ชัน "แปลกใหม่" เช่น y = x" ไม่ถือว่าเป็นเลขยกกำลังหรือกำลัง (บางครั้งเรียกว่าเลขชี้กำลัง)
หมายเหตุสำคัญประการที่สอง โดยปกติแล้วจะไม่พิจารณาฟังก์ชันเอ็กซ์โปเนนเชียลที่มีฐาน a = 1 หรือฐาน a ที่เป็นไปตามอสมการ a<0 (вы, конечно, помните, что выше, в определении показательной функции, оговорены условия: а >0 และ a ความจริงก็คือถ้า a = 1 ดังนั้นสำหรับค่าใด ๆ ของ x ความเท่าเทียมกัน Ix = 1 ยังคงอยู่ ดังนั้นฟังก์ชันเลขชี้กำลัง y = a" ที่มี a = 1 "เสื่อมลง" เป็นฟังก์ชันคงที่ y = 1 - นี่ ไม่น่าสนใจ ถ้า a = 0 ดังนั้น 0x = 0 สำหรับค่าบวกใดๆ ของ x นั่นคือ เราได้ฟังก์ชัน y = 0 ซึ่งกำหนดไว้สำหรับ x > 0 - นี่ก็ไม่น่าสนใจเช่นกัน หากในที่สุด a<0, то выражение а" имеет смысл лишь при целых значениях х, а мы все-таки предпочитаем рассматривать функции, определенные на сплошных промежутках.
ก่อนจะไปแก้ตัวอย่างต่อ โปรดทราบว่าฟังก์ชันเอ็กซ์โปเนนเชียลแตกต่างอย่างมากจากฟังก์ชันทั้งหมดที่คุณศึกษามาจนถึงตอนนี้ หากต้องการศึกษาวัตถุใหม่อย่างละเอียด คุณต้องพิจารณาจากมุมที่ต่างกัน ในสถานการณ์ที่ต่างกัน จึงจะมีตัวอย่างมากมาย
ตัวอย่างที่ 1
สารละลาย, a) เมื่อสร้างกราฟของฟังก์ชัน y = 2 x และ y = 1 ในระบบพิกัดเดียวแล้ว เราจะสังเกตเห็น (รูปที่ 203) ว่ากราฟทั้งสองมีจุดร่วมหนึ่งจุด (0; 1) ซึ่งหมายความว่าสมการ 2x = 1 มีรากเดียว x =0
ดังนั้น จากสมการ 2x = 2° เราจะได้ x = 0
b) เมื่อสร้างกราฟของฟังก์ชัน y = 2 x และ y = 4 ในระบบพิกัดเดียว เราจะสังเกตเห็น (รูปที่ 203) ว่ากราฟทั้งสองมีจุดร่วมหนึ่งจุด (2; 4) ซึ่งหมายความว่าสมการ 2x = 4 มีรากเดียว x = 2
ดังนั้น จากสมการ 2 x = 2 2 เราจะได้ x = 2
c) และ d) จากการพิจารณาแบบเดียวกัน เราสรุปได้ว่าสมการ 2 x = 8 มีรากเดียว และในการค้นหา ไม่จำเป็นต้องสร้างกราฟของฟังก์ชันที่เกี่ยวข้อง
เห็นได้ชัดว่า x = 3 เนื่องจาก 2 3 = 8 ในทำนองเดียวกัน เราก็พบรากเพียงอันเดียวของสมการ
ดังนั้น จากสมการ 2x = 2 3 เราได้ x = 3 และจากสมการ 2 x = 2 x เราได้ x = -4
e) กราฟของฟังก์ชัน y = 2 x ตั้งอยู่เหนือกราฟของฟังก์ชัน y = 1 สำหรับ x > 0 - สามารถอ่านได้อย่างชัดเจนในรูปที่ 1 203 ซึ่งหมายความว่าผลเฉลยของอสมการ 2x > 1 คือค่าช่วง
f) กราฟของฟังก์ชัน y = 2 x อยู่ใต้กราฟของฟังก์ชัน y = 4 ที่ x<2 - это хорошо читается по рис. 203. Значит, решением неравенства 2х <4служит промежуток
คุณอาจสังเกตเห็นว่าพื้นฐานสำหรับข้อสรุปทั้งหมดที่เกิดขึ้นเมื่อแก้ไขตัวอย่างที่ 1 คือคุณสมบัติของความซ้ำซ้อน (เพิ่มขึ้น) ของฟังก์ชัน y = 2 x การใช้เหตุผลที่คล้ายกันช่วยให้เราสามารถตรวจสอบความถูกต้องของทฤษฎีบทสองข้อต่อไปนี้ได้
สารละลาย.คุณสามารถดำเนินการดังนี้: สร้างกราฟของฟังก์ชัน y-3 x จากนั้นยืดออกจากแกน x ด้วยปัจจัย 3 จากนั้นยกกราฟผลลัพธ์ขึ้น 2 หน่วยมาตราส่วน แต่จะสะดวกกว่าถ้าใช้ข้อเท็จจริงที่ว่า 3- 3* = 3 * + 1 ดังนั้นให้สร้างกราฟของฟังก์ชัน y = 3 x * 1 + 2
มาดูกันว่าระบบพิกัดเสริมที่มีจุดกำเนิดอยู่ที่จุด (-1; 2) ดังที่เราเคยทำมาหลายครั้งในกรณีเช่นนี้ - เส้นประ x = - 1 และ 1x = 2 ในรูปที่ 1 207. มา “เชื่อมโยง” ฟังก์ชัน y=3* กับระบบพิกัดใหม่กันดีกว่า เมื่อต้องการทำเช่นนี้ ให้เลือกจุดควบคุมสำหรับฟังก์ชัน 
แต่เราจะไม่สร้างมันขึ้นมาแบบเก่า แต่ในระบบพิกัดใหม่ (จุดเหล่านี้ถูกทำเครื่องหมายไว้ในรูปที่ 207) จากนั้นเราจะสร้างเลขชี้กำลังจากจุด - นี่จะเป็นกราฟที่ต้องการ (ดูรูปที่ 207)
ในการค้นหาค่าที่ใหญ่ที่สุดและเล็กที่สุดของฟังก์ชันที่กำหนดในส่วน [-2, 2] เราใช้ประโยชน์จากข้อเท็จจริงที่ว่าฟังก์ชันที่กำหนดกำลังเพิ่มขึ้น ดังนั้นจึงใช้ค่าที่เล็กที่สุดและใหญ่ที่สุดตามลำดับที่ ปลายด้านซ้ายและขวาของเซ็กเมนต์
ดังนั้น:
ตัวอย่างที่ 4แก้สมการและอสมการ:
สารละลาย, a) ขอให้เราสร้างกราฟของฟังก์ชัน y=5* และ y=6-x ในระบบพิกัดเดียว (รูปที่ 208) พวกมันตัดกันที่จุดหนึ่ง ตัดสินจากภาพวาดนี่คือจุด (1; 5) การตรวจสอบแสดงให้เห็นว่าในความเป็นจริงแล้วจุด (1; 5) เป็นไปตามทั้งสมการ y = 5* และสมการ y = 6-x แอบซิสซาของจุดนี้ทำหน้าที่เป็นรากเดียวของสมการที่กำหนด
ดังนั้น สมการ 5 x = 6 - x มีรากเดียว x = 1
b) และ c) เลขชี้กำลัง y-5x อยู่เหนือเส้นตรง y=6-x ถ้า x>1 จะมองเห็นได้ชัดเจนในรูปที่ 1 208 ซึ่งหมายความว่าสามารถเขียนคำตอบของอสมการ 5*>6 ได้ดังนี้: x>1 และคำตอบของอสมการ 5x<6 - х можно записать так: х < 1.
คำตอบ: ก)x = 1; ข)x>1; ค)x<1.
ตัวอย่างที่ 5กำหนดให้มีฟังก์ชัน 
พิสูจน์ว่า 
สารละลาย.ตามเงื่อนไขที่เรามี
บทเรียนหมายเลข2
หัวข้อ: ฟังก์ชันเลขชี้กำลัง คุณสมบัติ และกราฟ
เป้า:ตรวจสอบคุณภาพของการเรียนรู้แนวคิดของ "ฟังก์ชันเลขชี้กำลัง" เพื่อพัฒนาทักษะในการจดจำฟังก์ชันเลขชี้กำลังโดยใช้คุณสมบัติและกราฟ สอนให้นักเรียนใช้รูปแบบการวิเคราะห์และกราฟิกในการบันทึกฟังก์ชันเลขชี้กำลัง จัดให้มีสภาพแวดล้อมการทำงานในห้องเรียน
อุปกรณ์:บอร์ดโปสเตอร์
แบบฟอร์มบทเรียน: บทเรียนในชั้นเรียน
ประเภทบทเรียน: บทเรียนภาคปฏิบัติ
ประเภทบทเรียน: บทเรียนทักษะและความสามารถการสอน
แผนการสอน
1. ช่วงเวลาขององค์กร
2.ทำงานอิสระและตรวจการบ้าน
3. การแก้ปัญหา
4. สรุป
5. การบ้าน
ความคืบหน้าของบทเรียน.
1. ช่วงเวลาขององค์กร :
สวัสดี เปิดสมุดบันทึกของคุณ จดวันที่ของวันนี้ และหัวข้อบทเรียน "ฟังก์ชันเลขชี้กำลัง" วันนี้เราจะมาศึกษาฟังก์ชันเลขชี้กำลัง คุณสมบัติ และกราฟกันต่อไป
2.ทำงานอิสระและตรวจการบ้าน .
เป้า:ตรวจสอบคุณภาพของความเชี่ยวชาญของแนวคิด "ฟังก์ชันเลขชี้กำลัง" และตรวจสอบความสมบูรณ์ของส่วนทฤษฎีของการบ้าน
วิธี:งานทดสอบการสำรวจหน้าผาก
ในการบ้าน คุณได้รับตัวเลขจากหนังสือโจทย์และย่อหน้าจากหนังสือเรียน เราจะไม่ตรวจสอบการใช้ตัวเลขจากหนังสือเรียนตอนนี้ แต่คุณจะต้องส่งสมุดบันทึกเมื่อสิ้นสุดบทเรียน ตอนนี้ทฤษฎีจะถูกทดสอบในรูปแบบของการทดสอบขนาดเล็ก งานจะเหมือนกันสำหรับทุกคน: คุณจะได้รับรายการฟังก์ชันต่างๆ คุณต้องค้นหาว่าฟังก์ชันใดบ้างที่บ่งบอกถึง (ขีดเส้นใต้) และถัดจากฟังก์ชันเอ็กซ์โปเนนเชียล คุณต้องเขียนว่าจะเพิ่มขึ้นหรือลดลง
ตัวเลือกที่ 1 คำตอบ ข) D) - เอ็กซ์โปเนนเชียลลดลง | ตัวเลือกที่ 2 คำตอบ D) - เอ็กซ์โปเนนเชียลลดลง ง) - เอ็กซ์โปเนนเชียลเพิ่มขึ้น |
ตัวเลือกที่ 3 คำตอบ ก) - เอ็กซ์โปเนนเชียลเพิ่มขึ้น ข) - เอ็กซ์โปเนนเชียลลดลง | ตัวเลือกที่ 4 คำตอบ ก) - เอ็กซ์โปเนนเชียลลดลง ใน) - เอ็กซ์โปเนนเชียลเพิ่มขึ้น |
ทีนี้มาจำกันว่าฟังก์ชันใดเรียกว่าเลขชี้กำลัง?
ฟังก์ชันของรูปแบบ ที่ไหน และ เรียกว่าฟังก์ชันเลขชี้กำลัง
ฟังก์ชั่นนี้มีขอบเขตอะไรบ้าง?
จำนวนจริงทั้งหมด
ฟังก์ชันเลขชี้กำลังมีพิสัยเท่าใด
จำนวนจริงบวกทั้งหมด
ลดลงถ้าฐานของกำลังมากกว่าศูนย์แต่น้อยกว่าหนึ่ง
ฟังก์ชันเอกซ์โปเนนเชียลลดลงในโดเมนคำจำกัดความในกรณีใด
เพิ่มขึ้นถ้าฐานของอำนาจมากกว่าหนึ่ง
3. การแก้ปัญหา
เป้า: เพื่อพัฒนาทักษะในการจำแนกฟังก์ชันเลขชี้กำลังโดยใช้คุณสมบัติและกราฟ สอนให้นักเรียนใช้รูปแบบการวิเคราะห์และกราฟิกในการเขียนฟังก์ชันเลขชี้กำลัง
วิธี: สาธิตโดยครูแก้ปัญหาทั่วไป งานปากเปล่า งานกระดานดำ งานในสมุดบันทึก บทสนทนาระหว่างครูกับนักเรียน
สามารถใช้คุณสมบัติของฟังก์ชันเลขชี้กำลังเมื่อเปรียบเทียบตัวเลข 2 ตัวขึ้นไป ตัวอย่างเช่น: หมายเลข 000 เปรียบเทียบค่าและถ้าก) 
..gif" width="37" height="20 src="> นี่เป็นงานที่ค่อนข้างซับซ้อน: เราจะต้องหารากที่สามของ 3 และ 9 แล้วเปรียบเทียบ แต่เรารู้ว่ามันเพิ่มขึ้น ในทางกลับกันหมายความว่าเมื่ออาร์กิวเมนต์เพิ่มขึ้นค่าของฟังก์ชันจะเพิ่มขึ้นนั่นคือเราเพียงแค่ต้องเปรียบเทียบค่าของอาร์กิวเมนต์และ เห็นได้ชัดว่า 
(สามารถสาธิตได้บนโปสเตอร์ที่แสดงฟังก์ชันเลขชี้กำลังที่เพิ่มขึ้น) และเสมอเมื่อแก้ไขตัวอย่างดังกล่าว คุณจะต้องกำหนดฐานของฟังก์ชันเลขชี้กำลังก่อน เปรียบเทียบกับ 1 กำหนดความซ้ำซ้อน และดำเนินการเปรียบเทียบอาร์กิวเมนต์ต่อไป ในกรณีของฟังก์ชันลดลง: เมื่ออาร์กิวเมนต์เพิ่มขึ้น ค่าของฟังก์ชันจะลดลง ดังนั้นเราจึงเปลี่ยนเครื่องหมายของความไม่เท่าเทียมกันเมื่อย้ายจากความไม่เท่าเทียมกันของอาร์กิวเมนต์ไปเป็นความไม่เท่าเทียมกันของฟังก์ชัน ต่อไปเราจะแก้ปากเปล่า: b) 
- 
ใน) 
- 
ช) 
- 
- หมายเลข 000 เปรียบเทียบตัวเลข ก) และ
ดังนั้นฟังก์ชันจึงเพิ่มขึ้นแล้ว
ทำไม ?
เพิ่มฟังก์ชันและ 
ดังนั้นฟังก์ชันจึงลดลงแล้ว 
ฟังก์ชันทั้งสองเพิ่มขึ้นตลอดขอบเขตคำจำกัดความ เนื่องจากเป็นเลขชี้กำลังที่มีฐานกำลังมากกว่าหนึ่ง
ความหมายเบื้องหลังคืออะไร?
เราสร้างกราฟ:
ฟังก์ชั่นไหนเพิ่มเร็วขึ้นเมื่อพยายาม https://pandia.ru/text/80/379/images/image062_0.gif" width="20 height=25" height="25">
ฟังก์ชั่นใดลดลงเร็วขึ้นเมื่อพยายาม https://pandia.ru/text/80/379/images/image062_0.gif" width="20 height=25" height="25">
ในช่วงระยะเวลาหนึ่ง ฟังก์ชันใดมีค่ามากกว่า ณ จุดใดจุดหนึ่ง
D), https://pandia.ru/text/80/379/images/image068_0.gif" width="69" height="57 src="> ก่อนอื่น เรามาดูขอบเขตของคำจำกัดความของฟังก์ชันเหล่านี้กันก่อน พวกเขาตรงกันหรือเปล่า?
ใช่ โดเมนของฟังก์ชันเหล่านี้เป็นจำนวนจริงทั้งหมด
ตั้งชื่อขอบเขตของแต่ละฟังก์ชันเหล่านี้
ช่วงของฟังก์ชันเหล่านี้ตรงกัน: จำนวนจริงบวกทั้งหมด
กำหนดประเภทของความน่าเบื่อของแต่ละฟังก์ชัน
ฟังก์ชันทั้งสามจะลดลงตลอดขอบเขตคำจำกัดความ เนื่องจากเป็นเลขชี้กำลังที่มีฐานของกำลังน้อยกว่าหนึ่งและมากกว่าศูนย์
มีจุดพิเศษอะไรอยู่ในกราฟของฟังก์ชันเลขชี้กำลัง?
ความหมายเบื้องหลังคืออะไร?
ไม่ว่าระดับของฟังก์ชันเลขชี้กำลังจะเป็นพื้นฐานของอะไรก็ตาม ถ้าเลขชี้กำลังมี 0 ค่าของฟังก์ชันนี้ก็จะเท่ากับ 1
เราสร้างกราฟ:
มาวิเคราะห์กราฟกัน กราฟของฟังก์ชันมีจุดตัดกันกี่จุด?
ฟังก์ชั่นใดลดลงเร็วขึ้นเมื่อพยายาม https://pandia.ru/text/80/379/images/image070.gif" width="41 height=57" height="57">
ฟังก์ชั่นไหนเพิ่มเร็วขึ้นเมื่อพยายาม https://pandia.ru/text/80/379/images/image070.gif" width="41 height=57" height="57">
ในช่วงระยะเวลาหนึ่ง ฟังก์ชันใดมีค่ามากกว่า ณ จุดใดจุดหนึ่ง
ในช่วงระยะเวลาหนึ่ง ฟังก์ชันใดมีค่ามากกว่า ณ จุดใดจุดหนึ่ง
เหตุใดฟังก์ชันเลขชี้กำลังที่มีฐานต่างกันจึงมีจุดตัดกันเพียงจุดเดียว
ฟังก์ชันเอ็กซ์โปเนนเชียลมีความซ้ำซากจำเจอย่างเคร่งครัดตลอดขอบเขตคำจำกัดความทั้งหมด ดังนั้นจึงสามารถตัดกันที่จุดเดียวเท่านั้น
งานต่อไปจะเน้นไปที่การใช้คุณสมบัตินี้ หมายเลข 000 ค้นหาค่าที่ใหญ่ที่สุดและน้อยที่สุดของฟังก์ชันที่กำหนดในช่วงเวลาที่กำหนด a) . ขอให้เราจำไว้อย่างเคร่งครัด ฟังก์ชั่นโมโนโทนิคใช้ค่าต่ำสุดและสูงสุดที่ส่วนท้ายของส่วนที่กำหนด และหากฟังก์ชันเพิ่มขึ้น ค่าที่ยิ่งใหญ่ที่สุดจะอยู่ทางด้านขวาสุดของเซ็กเมนต์ และค่าที่เล็กที่สุดจะอยู่ทางด้านซ้ายสุดของเซ็กเมนต์ (การสาธิตบนโปสเตอร์ โดยใช้ตัวอย่างฟังก์ชันเลขชี้กำลัง) หากฟังก์ชันลดลง ค่าที่ใหญ่ที่สุดจะอยู่ที่ปลายด้านซ้ายของเซ็กเมนต์ และค่าน้อยที่สุดจะอยู่ทางด้านขวาสุดของเซ็กเมนต์ (การสาธิตบนโปสเตอร์ โดยใช้ตัวอย่างฟังก์ชันเอ็กซ์โปเนนเชียล) ฟังก์ชั่นกำลังเพิ่มขึ้นเพราะฉะนั้นค่าที่เล็กที่สุดของฟังก์ชั่นจะอยู่ที่จุด https://pandia.ru/text/80/379/images/image075_0.gif" width="145" height="29" >. คะแนน ข ) 
, วี) 
d) แก้ไขสมุดบันทึกด้วยตัวเอง เราจะตรวจสอบด้วยวาจา
นักเรียนแก้ไขงานในสมุดบันทึก
|
ฟังก์ชั่นลดลง
|
ฟังก์ชั่นลดลง
|
ฟังก์ชั่นที่เพิ่มขึ้น
|
ค่าสูงสุดของฟังก์ชันบนเซ็กเมนต์
ค่าที่น้อยที่สุดของฟังก์ชันบนเซ็กเมนต์
ค่าที่น้อยที่สุดของฟังก์ชันบนเซ็กเมนต์
ค่าสูงสุดของฟังก์ชันบนเซ็กเมนต์- หมายเลข 000 ค้นหาค่าที่ใหญ่ที่สุดและน้อยที่สุดของฟังก์ชันที่กำหนดในช่วงเวลาที่กำหนด a) 
- งานนี้เกือบจะเหมือนกับงานก่อนหน้า แต่สิ่งที่ให้ไว้ที่นี่ไม่ใช่ส่วน แต่เป็นรังสี เรารู้ว่าฟังก์ชันกำลังเพิ่มขึ้น และไม่มีค่าที่ใหญ่ที่สุดหรือเล็กที่สุดในเส้นจำนวนทั้งหมด https://pandia.ru/text/80/379/images/image063_0.gif" width="68" height = "20"> และมีแนวโน้มที่ เช่น บนรังสี ฟังก์ชันที่มีแนวโน้มเป็น 0 แต่ไม่มีค่าต่ำสุด แต่มีค่ามากที่สุด ณ จุดนั้น 
- คะแนน ข) 
, วี) 
, ก) 
แก้โน้ตบุ๊กด้วยตัวเองเราจะตรวจสอบด้วยวาจา
