มุมระหว่างเส้นตรงสองเส้นเป็นวิธีพิกัด มุมระหว่างระนาบ

บทความนี้พูดถึงการหามุมระหว่างระนาบ หลังจากให้คำจำกัดความแล้ว เราจะให้ภาพประกอบกราฟิกและพิจารณาวิธีการโดยละเอียดในการค้นหาพิกัดโดยใช้วิธีนี้ เราได้สูตรสำหรับตัดระนาบซึ่งรวมถึงพิกัดของเวกเตอร์ปกติด้วย

ยานเดกซ์RTB R-A-339285-1

เนื้อหาจะใช้ข้อมูลและแนวคิดที่เคยศึกษาในบทความเกี่ยวกับเครื่องบินและเส้นในอวกาศ ขั้นแรก จำเป็นต้องไปยังการใช้เหตุผลที่ช่วยให้เรามีแนวทางที่แน่นอนในการกำหนดมุมระหว่างระนาบที่ตัดกันสองอัน

จะได้ระนาบที่ตัดกัน 2 อัน γ 1 และ γ 2 ทางแยกของพวกเขาจะใช้ชื่อค การสร้างระนาบ χ นั้นสัมพันธ์กับจุดตัดของระนาบเหล่านี้ ระนาบ χ ผ่านจุด M เป็นเส้นตรง c จุดตัดของระนาบ γ 1 และ γ 2 จะทำโดยใช้ระนาบ χ เราใช้ชื่อเส้นที่ตัดกัน γ 1 และ χ เป็นเส้น a และเส้นที่ตัดกัน γ 2 และ χ เป็นเส้น b เราพบว่าจุดตัดของเส้น a และ b เป็นจุด M

ตำแหน่งของจุด M ไม่ส่งผลต่อมุมระหว่างเส้นตัด a และ b และจุด M อยู่บนเส้น c ซึ่งเป็นจุดที่ระนาบ χ ผ่านไป

จำเป็นต้องสร้างระนาบ χ 1 ตั้งฉากกับเส้น c และแตกต่างจากระนาบ χ จุดตัดของระนาบ γ 1 และ γ 2 ด้วยความช่วยเหลือของ χ 1 จะใช้การกำหนดเส้น a 1 และ b 1

จะเห็นได้ว่าเมื่อสร้าง χ และ χ 1 เส้น a และ b ตั้งฉากกับเส้น c จากนั้น 1, b 1 จะตั้งฉากกับเส้น c การหาเส้นตรง a และ 1 ในระนาบ γ 1 ที่มีความตั้งฉากกับเส้นตรง c แล้วจึงถือว่าเส้นตรงทั้งสองขนานกัน ในทำนองเดียวกัน ตำแหน่งของ b และ b 1 ในระนาบ γ 2 ที่มีความตั้งฉากกับเส้นตรง c บ่งชี้ถึงความขนานกัน ซึ่งหมายความว่าจำเป็นต้องทำการถ่ายโอนระนาบ χ 1 ถึง χ แบบขนาน โดยที่เราจะได้เส้นตรงสองเส้นที่ตรงกัน a และ a 1, b และ b 1 เราพบว่ามุมระหว่างเส้นตัดกัน a และ b เท่ากับ 1 เท่ากับมุมตัดกันเส้น a และ b

ลองดูรูปด้านล่าง

ข้อเสนอนี้พิสูจน์ได้จากข้อเท็จจริงที่ว่าระหว่างเส้นตัดกัน a และ b มีมุมที่ไม่ขึ้นอยู่กับตำแหน่งของจุด M นั่นคือจุดตัดกัน เส้นเหล่านี้อยู่ในระนาบ γ 1 และ γ 2 ในความเป็นจริง มุมที่ได้นั้นถือได้ว่าเป็นมุมระหว่างระนาบที่ตัดกันสองอัน

มาดูการกำหนดมุมระหว่างระนาบที่ตัดกันที่มีอยู่ γ 1 และ γ 2 กัน

คำจำกัดความ 1

มุมระหว่างระนาบที่ตัดกัน γ 1 และ γ 2เรียกว่ามุมที่เกิดจากจุดตัดของเส้น a และ b โดยที่ระนาบ γ 1 และ γ 2 ตัดกับระนาบ χ ตั้งฉากกับเส้น c

พิจารณารูปด้านล่าง

คำวินิจฉัยอาจยื่นเป็นอย่างอื่นก็ได้ เมื่อระนาบ γ 1 และ γ 2 ตัดกัน โดยที่ c คือเส้นที่ระนาบทั้งสองตัดกัน ให้ทำเครื่องหมายจุด M โดยลากเส้น a และ b ตั้งฉากกับเส้น c และนอนอยู่ในระนาบ γ 1 และ γ 2 จากนั้นจึงเป็นมุมระหว่าง เส้น a และ b จะเป็นมุมระหว่างระนาบ ในทางปฏิบัติ สิ่งนี้ใช้ได้กับการสร้างมุมระหว่างระนาบ

เมื่อตัดกันมุมจะถูกสร้างขึ้นซึ่งมีค่าน้อยกว่า 90 องศานั่นคือการวัดระดับของมุมนั้นใช้ได้ในช่วงเวลาของประเภทนี้ (0, 90] ในเวลาเดียวกันระนาบเหล่านี้จะถูกเรียกว่าตั้งฉากถ้า มุมขวาจะเกิดขึ้นที่ทางแยก มุมระหว่าง ระนาบขนานถือว่าเท่ากับศูนย์

วิธีปกติในการค้นหามุมระหว่างระนาบที่ตัดกันคือการก่อสร้างเพิ่มเติม ซึ่งช่วยในการระบุได้อย่างแม่นยำ และสามารถทำได้โดยใช้เครื่องหมายของความเท่าเทียมกันหรือความคล้ายคลึงของรูปสามเหลี่ยม ไซน์ และโคไซน์ของมุม

ลองพิจารณาการแก้ปัญหาโดยใช้ตัวอย่างจากปัญหา Unified State Exam ของบล็อก C 2

ตัวอย่างที่ 1

เมื่อกำหนดรูปสี่เหลี่ยมด้านขนาน A B C D A 1 B 1 C 1 D 1 โดยที่ด้าน A B = 2, A D = 3, A A 1 = 7, จุด E หารด้าน A A 1 ในอัตราส่วน 4: 3 ค้นหามุมระหว่างระนาบ A B C และ B E D 1

สารละลาย

เพื่อความชัดเจนจำเป็นต้องวาดรูป เราเข้าใจแล้ว

การแสดงภาพเป็นสิ่งจำเป็นเพื่อให้สะดวกยิ่งขึ้นในการทำงานกับมุมระหว่างระนาบ

เรากำหนดเส้นตรงที่จุดตัดของระนาบ A B C และ B E D 1 เกิดขึ้น จุด B เป็นจุดร่วม ควรพบจุดตัดร่วมกันอีกจุดหนึ่ง ลองพิจารณาเส้นตรง D A และ D 1 E ซึ่งอยู่ในระนาบเดียวกัน A D D 1 ตำแหน่งของพวกมันไม่ได้บ่งบอกถึงความขนาน แต่หมายความว่าพวกมันมีจุดตัดร่วมกัน

อย่างไรก็ตาม เส้นตรง D A อยู่ในระนาบ A B C และ D 1 E ใน B E D 1 จากนี้เราจะได้เส้นตรงนั้น ดี เอและ ดี 1 อีมีจุดตัดร่วมกัน ซึ่งเป็นเรื่องธรรมดาสำหรับระนาบ A B C และ B E D 1 แสดงถึงจุดตัดกันของเส้น ดี เอและ D 1 E ตัวอักษร F. จากนี้เราจะได้ว่า B F เป็นเส้นตรงที่ระนาบ A B C และ B E D 1 ตัดกัน

ลองดูรูปด้านล่าง

เพื่อให้ได้คำตอบ จำเป็นต้องสร้างเส้นตรงที่อยู่ในระนาบ A B C และ B E D 1 ผ่านจุดที่อยู่บนเส้น B F และตั้งฉากกับจุดนั้น จากนั้นมุมที่เกิดขึ้นระหว่างเส้นตรงเหล่านี้ถือเป็นมุมที่ต้องการระหว่างระนาบ A B C และ B E D 1

จากนี้เราจะเห็นว่าจุด A คือเส้นโครงของจุด E ลงบนระนาบ A B C จำเป็นต้องวาดเส้นตรงที่ตัดกันเส้น B F เป็นมุมฉากที่จุด M จะเห็นได้ว่าเส้นตรง A M คือเส้นโครง ของเส้นตรง E M ลงบนระนาบ A B C ตามทฤษฎีบทเกี่ยวกับเส้นตั้งฉาก A M ⊥ B F พิจารณาภาพด้านล่าง

∠ A M E คือมุมที่ต้องการซึ่งเกิดจากระนาบ A B C และ B E D 1 จากผลลัพธ์สามเหลี่ยม A E M เราสามารถหาไซน์ โคไซน์ หรือแทนเจนต์ของมุม แล้วตามด้วยตัวมันเอง ก็ต่อเมื่อทราบทั้งสองด้านเท่านั้น ตามเงื่อนไขเราพบว่าความยาว A E พบได้ดังนี้ เส้นตรง A A 1 หารด้วยจุด E ในอัตราส่วน 4: 3 ซึ่งหมายความว่าความยาวรวมของเส้นตรงคือ 7 ส่วน แล้ว A E = 4 ส่วน เราพบ A M.

จำเป็นต้องพิจารณาสามเหลี่ยมมุมฉาก A B F เรามีมุมฉาก A ที่มีความสูง A M จากเงื่อนไข A B = 2 แล้วเราจะหาความยาว A F ได้ด้วยความคล้ายคลึงกันของรูปสามเหลี่ยม D D 1 F และ A E F เราจะได้ว่า A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

จำเป็นต้องค้นหาความยาวของด้าน B F ของสามเหลี่ยม A B F โดยใช้ทฤษฎีบทพีทาโกรัส เราพบว่า B F  = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 ความยาวของด้าน A M พบผ่านพื้นที่สามเหลี่ยม A B F เรามีว่าพื้นที่สามารถเท่ากับทั้ง S A B C = 1 2 · A B · A F และ S A B C = 1 2 · B F · A M

เราพบว่า A M = A B A F B F = 2 4 2 5 = 4 5 5

จากนั้นเราสามารถหาค่าแทนเจนต์ของมุมของสามเหลี่ยม A E M ได้ เราได้รับ:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

มุมที่ต้องการที่ได้จากจุดตัดของระนาบ A B C และ B E D 1 เท่ากับ a r c t g 5 จากนั้นเมื่อทำให้ง่ายขึ้น เราจะได้ a r c t g 5 = a r c sin 30 6 = a r c cos 6 6

คำตอบ: a rc t g 5 = a rc sin 30 6 = a rc cos 6 6 .

บางกรณีของการค้นหามุมระหว่างเส้นตัดกันระบุโดยใช้ระนาบพิกัด O x y z และวิธีการพิกัด มาดูกันดีกว่า

หากเกิดปัญหาเมื่อจำเป็นต้องค้นหามุมระหว่างระนาบที่ตัดกัน γ 1 และ γ 2 เราจะแสดงว่ามุมที่ต้องการเป็น α

จากนั้นระบบพิกัดที่กำหนดจะแสดงว่าเรามีพิกัดของเวกเตอร์ปกติของระนาบที่ตัดกัน γ 1 และ γ 2 จากนั้นเราแสดงว่า n 1 → = n 1 x, n 1 y, n 1 z เป็นเวกเตอร์ปกติของระนาบ γ 1 และ n 2 → = (n 2 x, n 2 y, n 2 z) - สำหรับ ระนาบ γ 2 ให้เราพิจารณาการกำหนดมุมโดยละเอียดระหว่างระนาบเหล่านี้ตามพิกัดของเวกเตอร์

จำเป็นต้องกำหนดเส้นตรงที่ระนาบγ 1 และγ 2 ตัดกับตัวอักษร c บนเส้นตรง c เรามีจุด M ซึ่งใช้วาดระนาบ χ ตั้งฉากกับ c ระนาบ χ ตามเส้น a และ b ตัดกันระนาบ γ 1 และ γ 2 ที่จุด M จากคำจำกัดความเป็นไปตามว่ามุมระหว่างระนาบที่ตัดกัน γ 1 และ γ 2 เท่ากับมุมของเส้นที่ตัดกัน a และ b ของระนาบเหล่านี้ ตามลำดับ

ในระนาบ χ เราพล็อตเวกเตอร์ปกติจากจุด M และแสดงเวกเตอร์เหล่านั้น n 1 → และ n 2 → เวกเตอร์ n 1 → อยู่บนเส้นตั้งฉากกับเส้น a และเวกเตอร์ n 2 → อยู่บนเส้นตั้งฉากกับเส้น b จากนี้เราจะได้ว่าระนาบที่กำหนด χ มี เวกเตอร์ปกติเส้น a เท่ากับ n 1 → และสำหรับเส้น b เท่ากับ n 2 → พิจารณารูปด้านล่าง

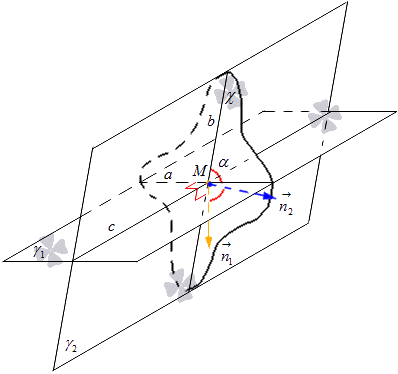
จากที่นี่เราได้สูตรสำหรับคำนวณไซน์ของมุมของเส้นตัดกันโดยใช้พิกัดของเวกเตอร์ เราพบว่าโคไซน์ของมุมระหว่างเส้นตรง a และ b เท่ากับโคไซน์ระหว่างระนาบที่ตัดกัน γ 1 และ γ 2 ซึ่งได้มาจาก สูตรคอสα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 ใช่ n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 โดยที่เรามี n 1 → = (n 1 x, n 1 y, n 1 z) และ n 2 → = (n 2 x, n 2 y, n 2 z) เป็นพิกัดของ เวกเตอร์ของเครื่องบินที่เป็นตัวแทน

มุมระหว่างเส้นตัดกันคำนวณโดยใช้สูตร

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

ตัวอย่างที่ 2

ตามเงื่อนไขจะได้ A B C D A 1 B 1 C 1 D 1 ที่ขนานกัน , โดยที่ A B = 2, A D = 3, A A 1 = 7 และจุด E แบ่งด้าน A A 1 4: 3 ค้นหามุมระหว่างระนาบ A B C และ B E D 1

สารละลาย

จากสภาพที่เห็นได้ชัดเจนว่าด้านข้างตั้งฉากกันเป็นคู่ ซึ่งหมายความว่าจำเป็นต้องแนะนำระบบพิกัด O x y z โดยมีจุดยอดที่จุด C และแกนพิกัด O x, O y, O z จำเป็นต้องกำหนดทิศทางไปทางด้านที่เหมาะสม พิจารณารูปด้านล่าง

เครื่องบินที่ตัดกัน เอ บี ซีและ บี อี ดี 1สร้างมุมที่หาได้โดยใช้สูตร α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 โดยที่ n 1 → = (n 1 x, n 1 y, n 1 z) และ n 2 → = (n 2 x, n 2 y, n 2 z ) เป็นเวกเตอร์ปกติของ เครื่องบินเหล่านี้ มีความจำเป็นต้องกำหนดพิกัด จากรูปเราจะเห็นว่าแกนพิกัด O x y เกิดขึ้นพร้อมกับระนาบ A B C ซึ่งหมายความว่าพิกัดของเวกเตอร์ปกติ k → เท่ากับค่า n 1 → = k → = (0, 0, 1)

เวกเตอร์ปกติของระนาบ B E D 1 ถือเป็นผลคูณเวกเตอร์ B E → และ B D 1 → โดยที่พิกัดของพวกมันจะพบได้จากพิกัดของจุดสุดขั้ว B, E, D 1 ซึ่งถูกกำหนดตามเงื่อนไขของ ปัญหา.

เราได้ B (0, 3, 0), D 1 (2, 0, 7) เนื่องจาก A E E A 1 = 4 3 จากพิกัดของจุด A 2, 3, 0, A 1 2, 3, 7 เราพบ E 2, 3, 4 เราพบว่า B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 · ผม → - 6 เจ → - 6 k → ⇔ n 2 → = (12 , - 6 , - 6)

จำเป็นต้องแทนที่พิกัดที่พบเป็นสูตรในการคำนวณมุมผ่านโคไซน์ส่วนโค้ง เราได้รับ

α = a rc cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a rc cos 6 6 6 = a rc cos 6 6

วิธีการประสานงานให้ผลลัพธ์ที่คล้ายกัน

คำตอบ: a rc cos 6 6 .

ปัญหาสุดท้ายได้รับการพิจารณาโดยมีเป้าหมายในการหามุมระหว่างระนาบที่ตัดกันโดยพิจารณาจากสมการของระนาบที่ทราบ

ตัวอย่างที่ 3

คำนวณไซน์ โคไซน์ของมุม และค่าของมุมที่เกิดจากเส้นตัดกันสองเส้น ซึ่งกำหนดไว้ในระบบพิกัด O x y z และกำหนดโดยสมการ 2 x - 4 y + z + 1 = 0 และ 3 y - z - 1 = 0.

สารละลาย

เมื่อศึกษาหัวข้อสมการเส้นตรงทั่วไปในรูปแบบ A x + B y + C z + D = 0 พบว่า A, B, C เป็นสัมประสิทธิ์เท่ากับพิกัดของเวกเตอร์ปกติ ซึ่งหมายความว่า n 1 → = 2, - 4, 1 และ n 2 → = 0, 3, - 1 เป็นเวกเตอร์ปกติของเส้นที่กำหนด

จำเป็นต้องแทนที่พิกัดของเวกเตอร์ปกติของเครื่องบินลงในสูตรในการคำนวณมุมที่ต้องการของระนาบที่ตัดกัน แล้วเราจะได้รับสิ่งนั้น

α = a rc cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a rc cos 13 210

จากตรงนี้ เราจะได้ว่าโคไซน์ของมุมอยู่ในรูป cos α = 13 210 แล้วมุมของเส้นที่ตัดกันจะไม่ป้าน เข้ามาทดแทน เอกลักษณ์ตรีโกณมิติเราพบว่าค่าไซน์ของมุมเท่ากับนิพจน์ ให้เราคำนวณและพบว่า

บาป α = 1 - cos 2 α = 1 - 13,210 = 41,210

คำตอบ:บาป α = 41,210, cos α = 13,210, α = a rc cos 13,210 = a rc sin 41,210

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดไฮไลต์แล้วกด Ctrl+Enter

บทความนี้เกี่ยวกับมุมระหว่างระนาบและวิธีการค้นหา ขั้นแรก ให้นิยามของมุมระหว่างระนาบสองระนาบและให้ภาพประกอบเป็นกราฟิก หลังจากนั้นหลักการของการค้นหามุมระหว่างระนาบที่ตัดกันสองอันโดยใช้วิธีพิกัดได้รับการวิเคราะห์และได้รับสูตรที่ช่วยให้คุณสามารถคำนวณมุมระหว่างระนาบที่ตัดกันโดยใช้พิกัดที่รู้จักของเวกเตอร์ปกติของระนาบเหล่านี้ โดยสรุปจะมีการแสดงวิธีแก้ปัญหาโดยละเอียดสำหรับปัญหาทั่วไป

การนำทางหน้า

มุมระหว่างระนาบ - คำจำกัดความ

ให้เราเสนอข้อโต้แย้งที่จะช่วยให้เราค่อยๆ เข้าใกล้การกำหนดมุมระหว่างระนาบที่ตัดกันสองอัน

ให้เราได้รับระนาบที่ตัดกันสองอัน และ ระนาบเหล่านี้ตัดกันเป็นเส้นตรงซึ่งเราแสดงด้วยตัวอักษร c ลองสร้างระนาบที่ผ่านจุด M ของเส้น c และตั้งฉากกับเส้น c ในกรณีนี้เครื่องบินจะตัดกันเครื่องบินและ ให้เราแสดงเส้นตรงที่ระนาบตัดกันเป็น a และเส้นตรงที่ระนาบตัดกันเป็น b แน่นอนว่า เส้น a และ b ตัดกันที่จุด M

เป็นเรื่องง่ายที่จะแสดงให้เห็นว่ามุมระหว่างเส้นตัด a และ b ไม่ได้ขึ้นอยู่กับตำแหน่งของจุด M บนเส้น c ที่เครื่องบินผ่านไป

ลองสร้างระนาบที่ตั้งฉากกับเส้น c และแตกต่างจากระนาบกัน ระนาบตัดกันด้วยระนาบและตามเส้นตรง ซึ่งเราแสดงว่าเป็น 1 และ b 1 ตามลำดับ

จากวิธีสร้างระนาบ เส้น a และ b ตั้งฉากกับเส้น c และเส้น a 1 และ b 1 ตั้งฉากกับเส้น c เนื่องจากเส้น a และ 1 อยู่ในระนาบเดียวกันและตั้งฉากกับเส้น c ดังนั้นเส้นทั้งสองจึงขนานกัน ในทำนองเดียวกัน เส้น b และ b 1 อยู่ในระนาบเดียวกันและตั้งฉากกับเส้น c ดังนั้นเส้นทั้งสองจึงขนานกัน ดังนั้นจึงเป็นไปได้ที่จะทำการถ่ายโอนเครื่องบินไปยังเครื่องบินแบบขนาน โดยที่เส้นตรง a 1 เกิดขึ้นพร้อมกับเส้นตรง a และเส้นตรง b กับเส้นตรง b 1 ดังนั้น มุมระหว่างเส้นตัดกันสองเส้น a 1 และ b 1 จึงเท่ากับมุมระหว่างเส้นตัดกัน a และ b

สิ่งนี้พิสูจน์ว่ามุมระหว่างเส้นตัด a และ b ที่อยู่ในระนาบที่ตัดกัน และไม่ขึ้นอยู่กับการเลือกจุด M ที่เครื่องบินผ่าน ดังนั้นจึงสมเหตุสมผลที่จะถือว่ามุมนี้เป็นมุมระหว่างระนาบสองระนาบที่ตัดกัน

ตอนนี้คุณสามารถแสดงคำจำกัดความของมุมระหว่างระนาบที่ตัดกันสองอันและ

คำนิยาม.

มุมระหว่างระนาบสองระนาบตัดกันเป็นเส้นตรงและ- นี่คือมุมระหว่างเส้นตัดกันสองเส้น a และ b ตามแนวระนาบและตัดกับระนาบที่ตั้งฉากกับเส้น c

คำจำกัดความของมุมระหว่างระนาบสองระนาบสามารถให้ความแตกต่างกันเล็กน้อย ถ้าบนเส้นตรง c ที่ระนาบและตัดกัน ให้ทำเครื่องหมายจุด M แล้วลากเส้นตรง a และ b ผ่านจุดนั้น ตั้งฉากกับเส้นตรง c และนอนอยู่ในระนาบ และตามลำดับ มุมระหว่างเส้นตรง a และ b คือมุมระหว่างระนาบและ โดยปกติในทางปฏิบัติ การก่อสร้างดังกล่าวจะดำเนินการเพื่อให้ได้มุมระหว่างระนาบ

เนื่องจากมุมระหว่างเส้นที่ตัดกันจะต้องไม่เกิน ตามคำจำกัดความที่ระบุไว้ว่าการวัดระดับของมุมระหว่างระนาบที่ตัดกันสองระนาบจะแสดงด้วยจำนวนจริงจากช่วงเวลา ในกรณีนี้จะเรียกว่าระนาบที่ตัดกัน ตั้งฉากถ้ามุมระหว่างพวกมันคือเก้าสิบองศา มุมระหว่างระนาบขนานไม่ได้ถูกกำหนดเลยหรือถือว่าเท่ากับศูนย์

การหามุมระหว่างระนาบสองระนาบที่ตัดกัน

โดยปกติ เมื่อหามุมระหว่างระนาบที่ตัดกันสองระนาบ คุณต้องสร้างเพิ่มเติมก่อนเพื่อดูเส้นตรงที่ตัดกัน มุมระหว่างนั้นจะเท่ากับมุมที่ต้องการ จากนั้นจึงเชื่อมต่อมุมนี้กับข้อมูลต้นฉบับโดยใช้การทดสอบความเท่าเทียมกัน ความคล้ายคลึงกัน การทดสอบ ทฤษฎีบทโคไซน์หรือคำจำกัดความของไซน์ โคไซน์ และแทนเจนต์ของมุม ในวิชาเรขาคณิต มัธยมปัญหาที่คล้ายกันเกิดขึ้น

ตามตัวอย่าง เราจะให้คำตอบสำหรับปัญหา C2 จากการสอบ Unified State ในวิชาคณิตศาสตร์ปี 2012 (เงื่อนไขถูกเปลี่ยนแปลงโดยเจตนา แต่ไม่ส่งผลกระทบต่อหลักการของการแก้ปัญหา) ในนั้น คุณแค่ต้องหามุมระหว่างระนาบสองระนาบที่ตัดกัน

ตัวอย่าง.

สารละลาย.

ก่อนอื่นมาวาดรูปกันก่อน

เรามาสร้างเพิ่มเติมเพื่อ "เห็น" มุมระหว่างระนาบกัน

ขั้นแรก เรามากำหนดเส้นตรงที่ระนาบ ABC และ BED 1 ตัดกัน จุด B เป็นหนึ่งในจุดร่วมของพวกเขา ลองหาจุดร่วมที่สองของระนาบเหล่านี้กัน เส้น DA และ D 1 E อยู่ในระนาบเดียวกันบวก 1 และไม่ขนานกันจึงตัดกัน ในทางกลับกัน เส้น DA อยู่ในระนาบ ABC และเส้น D 1 E - ในระนาบ BED 1 ดังนั้นจุดตัดของเส้น DA และ D 1 E จะเป็นจุดร่วมของระนาบ ABC และ BED 1 ลองลากเส้น DA และ D 1 E ต่อไปจนถึงทางแยกโดยระบุจุดตัดด้วยตัวอักษร F จากนั้น BF คือเส้นตรงที่ระนาบ ABC และ BED 1 ตัดกัน

ยังคงสร้างเส้นสองเส้นที่อยู่ในระนาบ ABC และ BED 1 ตามลำดับโดยผ่านจุดหนึ่งบนเส้น BF และตั้งฉากกับเส้น BF - มุมระหว่างเส้นเหล่านี้ตามคำจำกัดความจะเท่ากับมุมที่ต้องการระหว่าง เครื่องบิน ABC และ BED 1 มาทำกัน.

จุด A คือเส้นโครงของจุด E ลงบนระนาบ ABC ลองวาดเส้นตรงที่ตัดกัน BF ที่มุมขวาที่จุด M จากนั้น เส้นตรง AM คือเส้นโครงของเส้นตรง EM ลงบนระนาบ ABC และโดยทฤษฎีบทของเส้นตั้งฉากสามเส้น

ดังนั้น มุมที่ต้องการระหว่างระนาบ ABC และ BED 1 จึงเท่ากับ

เราสามารถหาไซน์ โคไซน์ หรือแทนเจนต์ของมุมนี้ (และมุมนั้นด้วย) จากสามเหลี่ยมมุมฉาก AEM ได้ถ้าเราทราบความยาวของด้านทั้งสองของมัน จากเงื่อนไขนี้ ง่ายต่อการค้นหาความยาว AE: เนื่องจากจุด E หารด้าน AA 1 ในอัตราส่วน 4 ต่อ 3 โดยนับจากจุด A และความยาวของด้าน AA 1 คือ 7 ดังนั้น AE = 4 ลองหาความยาว AM กัน

เมื่อต้องการทำเช่นนี้ ให้พิจารณา ABF สามเหลี่ยมมุมฉากที่มีมุมฉาก A โดยที่ AM คือความสูง โดยเงื่อนไข AB = 2 เราสามารถหาความยาวของด้าน AF ได้จากความคล้ายคลึงกันของสามเหลี่ยมมุมฉาก DD 1 F และ AEF:

เมื่อใช้ทฤษฎีบทพีทาโกรัส เราจะหาได้จากสามเหลี่ยม ABF เราพบความยาว AM ผ่านพื้นที่ของสามเหลี่ยม ABF: ด้านหนึ่งพื้นที่ของสามเหลี่ยม ABF เท่ากับ อีกด้านหนึ่ง , ที่ไหน .

จากสามเหลี่ยมมุมฉาก AEM เราก็ได้ .

จากนั้นมุมที่ต้องการระหว่างระนาบ ABC และ BED 1 จะเท่ากัน (โปรดทราบว่า ).

คำตอบ:

ในบางกรณี หากต้องการหามุมระหว่างระนาบสองระนาบที่ตัดกัน จะสะดวกในการตั้งค่า Oxyz และใช้วิธีการพิกัด มาหยุดอยู่แค่นั้น

ให้เรากำหนดภารกิจ: ค้นหามุมระหว่างระนาบที่ตัดกันสองอันและ ให้เราแสดงมุมที่ต้องการเป็น

เราจะสมมติว่าในระบบพิกัดสี่เหลี่ยมที่กำหนด Oxyz เรารู้พิกัดของเวกเตอร์ปกติของระนาบที่ตัดกัน และหรือมีโอกาสที่จะค้นหาพวกมัน อนุญาต คือเวกเตอร์ตั้งฉากของระนาบ และ คือเวกเตอร์ตั้งฉากของระนาบ เราจะแสดงวิธีหามุมระหว่างระนาบที่ตัดกันและผ่านพิกัดของเวกเตอร์ปกติของระนาบเหล่านี้

ให้เราแสดงเส้นตรงที่ระนาบและตัดกันเป็นค ผ่านจุด M บนเส้น c เราวาดระนาบตั้งฉากกับเส้น c ระนาบตัดกับระนาบและตามเส้น a และ b ตามลำดับ เส้น a และ b ตัดกันที่จุด M ตามคำนิยาม มุมระหว่างระนาบที่ตัดกัน และ เท่ากับมุมระหว่างเส้นที่ตัดกัน a และ b

ให้เราพล็อตเวกเตอร์และระนาบปกติ และจากจุด M ในระนาบ ในกรณีนี้ เวกเตอร์อยู่บนเส้นตั้งฉากกับเส้น a และเวกเตอร์อยู่บนเส้นที่ตั้งฉากกับเส้น b ดังนั้น ในระนาบ เวกเตอร์คือเวกเตอร์ตั้งฉากของเส้น a และเป็นเวกเตอร์ตั้งฉากของเส้น b

ในบทความเรื่องการหามุมระหว่างเส้นที่ตัดกัน เราได้รับสูตรที่ช่วยให้คำนวณโคไซน์ของมุมระหว่างเส้นที่ตัดกันโดยใช้พิกัดของเวกเตอร์ปกติ ดังนั้น โคไซน์ของมุมระหว่างเส้น a และ b และด้วยเหตุนี้ โคไซน์ของมุมระหว่างระนาบที่ตัดกันและหาได้จากสูตรโดยที่ และ เป็นเวกเตอร์ปกติของระนาบ และ ตามลำดับ จากนั้นจึงคำนวณเป็น .

ลองแก้ตัวอย่างก่อนหน้านี้โดยใช้วิธีพิกัด

ตัวอย่าง.

ให้ ABCDA 1 B 1 C 1 D 1 ที่มีรูปสี่เหลี่ยมผืนผ้าขนานกัน โดยที่ AB = 2, AD = 3, AA 1 = 7 และจุด E หารด้าน AA 1 ในอัตราส่วน 4 ต่อ 3 โดยนับจากจุด A ค้นหามุมระหว่างระนาบ ABC และ BED 1

สารละลาย.

เนื่องจากด้านข้างของสี่เหลี่ยมด้านขนานที่จุดยอดหนึ่งตั้งฉากกันเป็นคู่ จึงสะดวกที่จะแนะนำระบบพิกัดสี่เหลี่ยม Oxyz ดังต่อไปนี้: จัดตำแหน่งจุดเริ่มต้นให้ตรงกับจุดยอด C และกำหนดแกนพิกัด Ox, Oy และ Oz ไปตามด้าน CD , CB และ CC 1 ตามลำดับ

มุมระหว่างระนาบ ABC และ BED 1 สามารถพบได้ผ่านพิกัดของเวกเตอร์ปกติของระนาบเหล่านี้โดยใช้สูตร โดยที่ และ คือเวกเตอร์ปกติของระนาบ ABC และ BED 1 ตามลำดับ ลองหาพิกัดของเวกเตอร์ปกติกัน

ขนาดของมุมระหว่างระนาบสองระนาบที่แตกต่างกันสามารถกำหนดได้สำหรับตำแหน่งสัมพัทธ์ของระนาบ

กรณีเล็กๆ น้อยๆ หากเครื่องบินขนานกัน จากนั้นมุมระหว่างพวกมันจะถือว่าเท่ากับศูนย์

กรณีที่ไม่สำคัญหากเครื่องบินตัดกัน คดีนี้เป็นเรื่องที่ต้องหารือกันต่อไป ก่อนอื่น เราต้องการแนวคิดเรื่องมุมไดฮีดรัล

9.1 มุมไดฮีดรัล

มุมไดฮีดรัลคือระนาบครึ่งระนาบสองอันที่มีเส้นตรงร่วม (ซึ่งเรียกว่าขอบของมุมไดฮีดรัล) ในรูป 50 แสดงมุมไดฮีดรัลที่เกิดจากระนาบครึ่งระนาบ และ; ขอบของมุมไดฮีดรัลนี้คือเส้นตรง a ซึ่งพบได้ทั่วไปในระนาบครึ่งระนาบเหล่านี้

ข้าว. 50. มุมไดฮีดรัล

มุมไดฮีดรัลสามารถวัดเป็นองศาหรือเรเดียนได้ในคำเดียว โดยป้อนค่าเชิงมุมของมุมไดฮีดรัล ทำได้ดังนี้

บนขอบของมุมไดฮีดรัลที่เกิดจากระนาบครึ่งและเราหาจุด M โดยพลการ ให้เราวาดรังสี MA และ MB ตามลำดับโดยนอนอยู่ในระนาบครึ่งเหล่านี้และตั้งฉากกับขอบ (รูปที่ 51)

ข้าว. 51. มุมไดฮีดรัลเชิงเส้น

มุมที่ได้ AMB คือมุมเชิงเส้นของมุมไดฮีดรัล มุม " = \AMB คือค่าเชิงมุมของมุมไดฮีดรัลของเราอย่างแน่นอน

คำนิยาม. ขนาดเชิงมุมของมุมไดฮีดรัลคือขนาดของมุมเชิงเส้นของมุมไดฮีดรัลที่กำหนด

มุมเชิงเส้นทั้งหมดของมุมไดฮีดรัลจะเท่ากัน (ท้ายที่สุดแล้วจะได้มาจากกันและกันโดยการเลื่อนแบบขนาน) นั่นเป็นเหตุผล คำจำกัดความนี้ถูกต้อง: ค่า " ไม่ได้ขึ้นอยู่กับตัวเลือกเฉพาะของจุด M บนขอบของมุมไดฮีดรัล

9.2 การกำหนดมุมระหว่างระนาบ

เมื่อระนาบสองระนาบตัดกัน จะได้มุมไดฮีดรัลสี่มุม หากทุกอันมีขนาดเท่ากัน (อันละ 90 อัน) ระนาบนั้นจะถูกเรียกว่าตั้งฉาก มุมระหว่างระนาบคือ 90

ถ้ามุมไดฮีดรัลไม่เท่ากันทั้งหมด (นั่นคือ มีสองมุมแหลมและสองมุมป้าน) ดังนั้นมุมระหว่างระนาบจะเป็นค่าของมุมไดฮีดรัลเฉียบพลัน (รูปที่ 52)

ข้าว. 52. มุมระหว่างระนาบ

9.3 ตัวอย่างการแก้ปัญหา

ลองดูปัญหาสามประการ อย่างแรกนั้นง่าย ส่วนที่สองและสามอยู่ที่ประมาณระดับ C2 ในการสอบ Unified State ในวิชาคณิตศาสตร์

ปัญหาที่ 1. ค้นหามุมระหว่างสองหน้าของจัตุรมุขธรรมดา

สารละลาย. ให้ ABCD เป็นจัตุรมุขธรรมดา ขอให้เราวาดค่ามัธยฐาน AM และ DM ของใบหน้าที่เกี่ยวข้อง รวมถึงความสูงของจัตุรมุข DH (รูปที่ 53)

ข้าว. 53. ไปที่ภารกิจที่ 1

เนื่องจากค่ามัธยฐาน AM และ DM จึงเป็นความสูงของสามเหลี่ยมด้านเท่า ABC และ DBC เช่นกัน ดังนั้น มุม " = \AMD คือมุมเชิงเส้นของมุมไดฮีดรัลที่เกิดจากหน้า ABC และ DBC เราพบได้จากสามเหลี่ยม DHM:

			01.00 น

คำตอบ: อาร์คคอส 1 3 .

ปัญหาที่ 2 ในพีระมิดรูปสี่เหลี่ยมจัตุรัสปกติ SABCD (มีจุดยอด S) ขอบด้านข้างจะเท่ากับด้านข้างของฐาน จุด K คือจุดกึ่งกลางของขอบ SA ค้นหามุมระหว่างระนาบ

สารละลาย. เส้น BC ขนานกับ AD และขนานกับระนาบ ADS ดังนั้น ระนาบ KBC จะตัดระนาบ ADS ตามเส้นตรง KL ขนานกับ BC (รูปที่ 54)

ข้าว. 54. ไปที่ภารกิจที่ 2

ในกรณีนี้ KL จะขนานกับเส้น AD ด้วย ดังนั้น KL เส้นกลาง ADS สามเหลี่ยม และจุด L คือจุดกึ่งกลางของ DS

ลองหาความสูงของปิรามิด SO ให้ N เป็นจุดศูนย์กลางของ DO ดังนั้น LN คือเส้นกลางของสามเหลี่ยม DOS และด้วยเหตุนี้ LN k SO ซึ่งหมายความว่า LN ตั้งฉากกับระนาบ ABC

จากจุด N เราลดค่า NM ตั้งฉากลงเป็นเส้นตรง BC เส้นตรง NM จะเป็นเส้นโครงของ LM ที่เอียงไปบนระนาบ ABC จากทฤษฎีบททั้งสามตั้งฉาก จะได้ว่า LM ตั้งฉากกับ BC เช่นกัน

ดังนั้น มุม " = \LMN คือมุมเชิงเส้นของมุมไดฮีดรัลที่เกิดจากครึ่งระนาบ KBC และ ABC เราจะมองหามุมนี้จากสามเหลี่ยมมุมฉาก LMN

ให้ขอบของพีระมิดเท่ากับ a ก่อนอื่นเราจะหาความสูงของปิรามิด:

ดังนั้น=หน้า

สารละลาย. ให้ L เป็นจุดตัดของเส้น A1 K และ AB จากนั้นระนาบ A1 KC ตัดระนาบ ABC ตามเส้นตรง CL (รูปที่ 55)

ก ค

ข้าว. 55. ถึงปัญหา 3

สามเหลี่ยม A1 B1 K และ KBL เท่ากันที่ขาและมุมแหลม ดังนั้นขาอีกข้างจะเท่ากัน: A1 B1 = BL

พิจารณาสามเหลี่ยม ACL ในนั้น BA = BC = BL มุม CBL คือ 120; ดังนั้น \BCL = 30 นอกจากนี้ \BCA = 60 ดังนั้น \ACL = \BCA + \BCL = 90

แล้วแอลซีล่ะ? เครื่องปรับอากาศ แต่เส้น AC ทำหน้าที่เป็นเส้นโครงของเส้น A1 C บนระนาบ ABC จากทฤษฎีบทของเส้นตั้งฉากสามเส้น เราจะสรุปได้ว่า LC ? A1 ซี.

ดังนั้น มุม A1 CA คือมุมเชิงเส้นของมุมไดฮีดรัลที่เกิดจากระนาบครึ่ง A1 KC และ ABC นี่คือมุมที่ต้องการ จากสามเหลี่ยมหน้าจั่ว A1 AC เราจะเห็นว่ามันเท่ากับ 45

ปัญหา 1.6. ให้ลูกบาศก์ M, N, P - จุดกึ่งกลางของขอบ, AB, BC ตามลำดับ ค้นหามุมระหว่างระนาบ (MNP) และ

ก) ให้เราแนะนำระบบพิกัดคาร์ทีเซียนสี่เหลี่ยมตามที่ระบุในรูปที่ 17 ความยาวของขอบของลูกบาศก์สามารถเลือกได้โดยพลการ เนื่องจากด้วยความคล้ายคลึงกัน มุมระหว่างระนาบจะไม่เปลี่ยนแปลง ตัวอย่างเช่น จะสะดวกที่จะหาความยาวของขอบของลูกบาศก์เท่ากับ 2

สัมพันธ์กับระบบพิกัดที่เลือก เราจะค้นหาพิกัดของจุดและเวกเตอร์:

b) อนุญาต เป็นเวกเตอร์ตั้งฉากของระนาบ

ในกรณีนี้เป็นไปตามเงื่อนไข

ในทำนองเดียวกัน ถ้า เป็นเวกเตอร์ปกติของระนาบ แล้ว

ค) ถ้าเช่นนั้น

คำตอบ:

ปัญหา 1.7. ที่ฐานของพีระมิดรูปสามเหลี่ยมปกติ SABC จะอยู่ในลักษณะปกติ โดยมีด้านเท่ากับ 2 ขอบ SA ตั้งฉากกับระนาบของฐาน และ SA = 1 จุด P, Q คือจุดกึ่งกลางของขอบ SB, NE ตามลำดับ ระนาบขนานกับเส้น SC และ AB และระนาบขนานกับเส้น AQ และ CP กำหนดขนาดของมุมระหว่างระนาบและ

ก) ให้เราเลือกระบบพิกัดคาร์ทีเซียนสี่เหลี่ยมดังแสดงในรูปที่ 18 ในระบบพิกัดที่เลือกเรามี:

b) คือเวกเตอร์ตั้งฉากของระนาบขนานกับเส้น SC และ AB จากนั้นจึงตรงตามเงื่อนไข:

c) ขอให้เราเขียนแทนด้วยระนาบที่ขนานกับเส้น AQ และ CP และด้วยเวกเตอร์ตั้งฉาก ในกรณีนี้เราได้รับระบบของแบบฟอร์ม

ปัญหาที่ 1 ฐานของปริซึมสี่เหลี่ยมมุมฉาก ABCDA 1 B 1 C 1 D 1 เป็นรูปสี่เหลี่ยมผืนผ้า ABCD โดยที่ AB = 5, AD = 11 จงหาค่าแทนเจนต์ของมุมระหว่างระนาบของฐานของปริซึมกับ ระนาบที่ผ่านตรงกลางขอบ AD ตั้งฉากกับเส้นตรง BD 1 ถ้าระยะห่างระหว่างเส้นตรง AC และ B 1 D 1 เท่ากับ 12 วิธีแก้ ขอแนะนำระบบพิกัด B(0;0;0), A(5;0;0), C(0;11;0), D 1 (5;11;12) พิกัดของเส้นปกติถึงระนาบส่วน: พิกัดของเส้นปกติถึง ระนาบฐาน: – มุมแหลม จากนั้น D A B C D1D1 A1A1 B1B1 C1C1 x y z N มุมระหว่างระนาบ คำตอบ: 0.5 เนนาเชวา เอ็น.จี. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 2 ที่ฐานของพีระมิดรูปสามเหลี่ยม SABC มีรูปสามเหลี่ยม ABC อยู่ มุม A เป็นเส้นตรง AC = 8, BC = 219 ความสูงของปิรามิด SA คือ 6 จุด M อยู่บนขอบ AC ดังนั้น AM = 2 ระนาบ α ถูกลากผ่านจุด M, จุดยอด B และจุด N - จุดกึ่งกลางของ เอดจ์ เอสซี ค้นหามุมไดฮีดรัลที่เกิดจากระนาบ α และระนาบของฐานปิรามิด A S x B C M N y z วิธีแก้ปัญหา ขอแนะนำระบบพิกัด จากนั้น A (0;0;0), C (0;8;0), M (0;2;0), N (0;4;3), S (0;0;6), ปกติกับเครื่องบิน (ABC) เวกเตอร์ ระนาบปกติ (PMN) มุมระหว่างระนาบ คำตอบ: 60° สมการระนาบ (ВМN): Nenasheva N.G. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 3 ฐานของพีระมิดรูปสี่เหลี่ยม PABCD เป็นรูปสี่เหลี่ยมจัตุรัสที่มีด้านเท่ากับ 6 ขอบด้าน PD ตั้งฉากกับระนาบของฐาน และเท่ากับ 6 จงหามุมระหว่างระนาบ (BDP) และ (BCP) สารละลาย. 1. ลองวาดค่ามัธยฐาน DF ของสามเหลี่ยมหน้าจั่ว CDP (BC = PD = 6) ดังนั้น DF PC และจากข้อเท็จจริงที่ว่า BC (CDP) จะเป็นไปตามนั้น DF BC ซึ่งหมายถึง DF (PCB) A D C B P F 2 เนื่องจาก AC DB และ AC DP จากนั้น AC (BDP) 3 ดังนั้นมุมระหว่างระนาบ (BDP) และ (BCP) หาได้จากเงื่อนไข คือ มุมระหว่างระนาบ Nenasheva N.G. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 3 ฐานของพีระมิดรูปสี่เหลี่ยม PABCD เป็นรูปสี่เหลี่ยมจัตุรัสที่มีด้านเท่ากับ 6 ขอบด้าน PD ตั้งฉากกับระนาบของฐาน และเท่ากับ 6 จงหามุมระหว่างระนาบ (BDP) และ (BCP) โซลูชัน.4. เรามาเลือกระบบพิกัดกันดีกว่า พิกัดของจุด: 5. จากนั้นเวกเตอร์จะมีพิกัดต่อไปนี้: 6. เมื่อคำนวณค่าแล้วเราจะพบ: จากนั้น A D C B P F z x y มุมระหว่างระนาบ คำตอบ: Nenasheva N.G. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 4 ในหน่วยลูกบาศก์ ABCDA 1 B 1 C 1 D 1 ให้ค้นหามุมระหว่างระนาบ (AD 1 E) และ (D 1 FC) โดยที่จุด E และ F เป็นจุดกึ่งกลางของขอบ A 1 B 1 และ ข 1 ค 1 ตามลำดับ วิธีแก้ปัญหา: 1. เรามาแนะนำระบบพิกัดสี่เหลี่ยมและกำหนดพิกัดของจุด: 2. มาสร้างสมการของระนาบ (AD 1 E): 3. มาสร้างสมการของระนาบ (D 1 FC): - ปกติกันเถอะ เวกเตอร์ของเครื่องบิน (ค.ศ. 1 จ) - เวกเตอร์ปกติของเครื่องบิน (D 1 FC) มุมระหว่างระนาบ x y z Nenasheva N.G. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 4 ในหน่วยลูกบาศก์ ABCDA 1 B 1 C 1 D 1 ให้ค้นหามุมระหว่างระนาบ (AD 1 E) และ (D 1 FC) โดยที่จุด E และ F เป็นจุดกึ่งกลางของขอบ A 1 B 1 และ ข 1 ค 1 ตามลำดับ วิธีแก้ปัญหา: 4. ค้นหาโคไซน์ของมุมระหว่างระนาบโดยใช้สูตร คำตอบ: มุมระหว่างระนาบ x y z Nenasheva N.G. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 5. ส่วนที่เชื่อมต่อศูนย์กลางของฐานของปิรามิดสามเหลี่ยมปกติกับตรงกลางของขอบด้านข้าง เท่ากับด้านข้างบริเวณ ค้นหามุมระหว่างด้านประชิดของพีระมิด วิธีแก้: x y z 1. ขอแนะนำระบบพิกัดสี่เหลี่ยมและกำหนดพิกัดของจุด A, B, C: K ให้ด้านฐานเท่ากับ 1 เพื่อความแน่นอน ให้พิจารณาใบหน้า SAC และ SBC 2. มาหาพิกัดกัน ของจุด S: E มุมระหว่างระนาบ Nenasheva N.G. . ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 5 ส่วนที่เชื่อมต่อศูนย์กลางของฐานของปิรามิดสามเหลี่ยมปกติกับตรงกลางของขอบด้านข้างจะเท่ากับด้านข้างของฐาน ค้นหามุมระหว่างด้านประชิดของพีระมิด วิธีแก้: x y z K E SO เราหาได้จาก OSB: มุมระหว่างระนาบ Nenasheva N.G. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 5 ส่วนที่เชื่อมต่อศูนย์กลางของฐานของปิรามิดสามเหลี่ยมปกติกับตรงกลางของขอบด้านข้างจะเท่ากับด้านข้างของฐาน ค้นหามุมระหว่างด้านประชิดของพีระมิด วิธีแก้: x y z K E 3. สมการระนาบ (SAC): - เวกเตอร์ปกติของระนาบ (SAC) 4. สมการระนาบ (SBC): - เวกเตอร์ปกติของระนาบ (SBC) มุมระหว่างระนาบ Nenasheva N.G. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985

ปัญหาที่ 5 ส่วนที่เชื่อมต่อศูนย์กลางของฐานของปิรามิดสามเหลี่ยมปกติกับตรงกลางของขอบด้านข้างจะเท่ากับด้านข้างของฐาน ค้นหามุมระหว่างด้านประชิดของพีระมิด วิธีแก้ปัญหา: x y z K E 5. ค้นหาโคไซน์ของมุมระหว่างระนาบโดยใช้สูตร คำตอบ: มุมระหว่างระนาบ Nenasheva N.G. ครูคณิตศาสตร์ GBOU โรงเรียนมัธยม 985