คุณสมบัติของมุมที่อยู่ติดกันของสี่เหลี่ยมด้านขนาน การคำนวณพื้นที่ของรูป

⁰

สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมขนมเปียกปูนที่มีด้านตรงข้ามขนานกันเป็นคู่ รูปต่อไปนี้แสดงรูปสี่เหลี่ยมด้านขนาน ABCD มีด้าน AB ขนานกับด้าน CD และด้าน BC ขนานกับด้าน AD

ดังที่คุณคงเดาได้ สี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนนูน ลองพิจารณาคุณสมบัติพื้นฐานของรูปสี่เหลี่ยมด้านขนานกัน

คุณสมบัติของสี่เหลี่ยมด้านขนาน

1. ในรูปสี่เหลี่ยมด้านขนาน มุมตรงข้ามและด้านตรงข้ามก็เท่ากัน มาพิสูจน์คุณสมบัตินี้กัน - พิจารณาสี่เหลี่ยมด้านขนานที่แสดงในรูปต่อไปนี้

เส้นทแยงมุม BD แบ่งออกเป็นสามเหลี่ยมสองรูปเท่าๆ กัน: ABD และ CBD พวกมันจะเท่ากันตลอดด้าน BD และมุมสองมุมที่อยู่ติดกัน เนื่องจากมุมที่วางขวางที่เส้นตัด BD ของเส้นคู่ขนาน BC และ AD และ AB และ CD ตามลำดับ ดังนั้น AB = ซีดี และ
พ.ศ. = ค.ศ. และจากความเท่าเทียมกันของมุม 1, 2, 3 และ 4 จะได้ว่ามุม A = มุม 1 + มุม 3 = มุม 2 + มุม 4 = มุม C

2. เส้นทแยงมุมของสี่เหลี่ยมด้านขนานจะถูกแบ่งครึ่งตามจุดตัด ให้จุด O เป็นจุดตัดของเส้นทแยงมุม AC และ BD ของสี่เหลี่ยมด้านขนาน ABCD

จากนั้นสามเหลี่ยม AOB และสามเหลี่ยม COD จะเท่ากัน ตามแนวด้านข้างและมุมสองมุมที่อยู่ติดกัน (AB = CD เนื่องจากสิ่งเหล่านี้เป็นด้านตรงข้ามของสี่เหลี่ยมด้านขนาน และ angle1 = angle2 และ angle3 = angle4 เป็นเหมือนมุมขวางเมื่อเส้น AB และ CD ตัดกับเซแคนต์ AC และ BD ตามลำดับ) จากนี้จึงเป็นไปตามที่ AO = OC และ OB = OD ซึ่งจำเป็นต้องพิสูจน์

คุณสมบัติหลักทั้งหมดแสดงไว้ในสามรูปต่อไปนี้

สรุปบทเรียน

พีชคณิตเกรด 8

ครูสิซอย อ.ก.

โรงเรียน 2371

หัวข้อบทเรียน: “สี่เหลี่ยมด้านขนานและคุณสมบัติของมัน”

ประเภทบทเรียน: รวม

วัตถุประสงค์ของบทเรียน:

1) ตรวจสอบให้แน่ใจว่ามีการดูดซับแนวคิดใหม่ - สี่เหลี่ยมด้านขนานและคุณสมบัติของมัน

2) พัฒนาทักษะและความสามารถในการแก้ปัญหาทางเรขาคณิตอย่างต่อเนื่อง

3) การพัฒนาวัฒนธรรมการพูดทางคณิตศาสตร์

แผนการเรียน:

1. เวลาจัดงาน

(สไลด์ 1)

สไลด์นี้แสดงคำกล่าวของ Lewis Carroll นักเรียนจะได้รับแจ้งเกี่ยวกับจุดประสงค์ของบทเรียน มีการตรวจสอบความพร้อมของนักเรียนสำหรับบทเรียน

2. การอัพเดตความรู้

(สไลด์ 2)

บนกระดานมีงานสำหรับงานช่องปาก ครูเชิญชวนให้นักเรียนคิดถึงปัญหาเหล่านี้และยกมือให้ผู้ที่เข้าใจวิธีแก้ปัญหา หลังจากแก้ไขปัญหาสองข้อแล้ว นักเรียนคนหนึ่งจะถูกเรียกไปที่กระดานเพื่อพิสูจน์ทฤษฎีบทเกี่ยวกับผลรวมของมุม โดยจะเป็นผู้ก่อสร้างเพิ่มเติมตามแบบอย่างอิสระและพิสูจน์ทฤษฎีบทด้วยวาจา

นักเรียนใช้สูตรหาผลรวมของมุมของรูปหลายเหลี่ยม:

3. ส่วนหลัก

(สไลด์ 3)

นิยามของสี่เหลี่ยมด้านขนานบนกระดาน ครูพูดถึงตัวเลขใหม่และกำหนดคำจำกัดความโดยอธิบายที่จำเป็นโดยใช้ภาพวาด จากนั้น ในส่วนของตารางหมากรุกของงานนำเสนอ เขาแสดงวิธีการวาดรูปสี่เหลี่ยมด้านขนานโดยใช้มาร์กเกอร์และไม้บรรทัด (เป็นไปได้หลายกรณี)

(สไลด์ 4)

ครูกำหนดคุณสมบัติแรกของรูปสี่เหลี่ยมด้านขนาน เชิญชวนให้นักเรียนเล่าจากภาพวาดว่าได้รับอะไรและต้องพิสูจน์อะไร หลังจากนั้นงานที่กำหนดจะปรากฏบนกระดาน นักเรียนเดา (อาจด้วยความช่วยเหลือของครู) ว่าความเท่าเทียมกันที่ต้องการจะต้องพิสูจน์ผ่านความเท่าเทียมกันของสามเหลี่ยมซึ่งสามารถหาได้จากการวาดเส้นทแยงมุม (เส้นทแยงมุมปรากฏบนกระดาน) จากนั้น นักเรียนเดาว่าเหตุใดสามเหลี่ยมจึงเท่ากันและตั้งชื่อเครื่องหมายว่าสามเหลี่ยมเท่ากัน (รูปร่างที่สอดคล้องกันจะปรากฏขึ้น) พวกเขาสื่อสารข้อเท็จจริงที่จำเป็นในการทำให้สามเหลี่ยมเท่ากันด้วยวาจา (ภาพที่สอดคล้องกันจะปรากฏขึ้นตามที่พวกเขาตั้งชื่อ) จากนั้นให้นักเรียนกำหนดคุณสมบัติ สามเหลี่ยมเท่ากันปรากฏเป็นจุดที่ 3 ของการพิสูจน์ จากนั้นพวกเขาก็ทำการพิสูจน์ทฤษฎีบทด้วยปากเปล่าโดยอิสระ

(สไลด์ 5)

ครูกำหนดคุณสมบัติที่สองของสี่เหลี่ยมด้านขนาน รูปสี่เหลี่ยมด้านขนานปรากฏบนกระดาน ครูแนะนำให้ใช้ภาพเพื่อบอกว่าอะไรให้อะไรและอะไรต้องพิสูจน์ หลังจากที่นักเรียนรายงานสิ่งที่ได้รับและสิ่งที่ต้องพิสูจน์อย่างถูกต้องแล้ว เงื่อนไขของทฤษฎีบทก็จะปรากฏขึ้น นักเรียนเดาว่าความเท่าเทียมกันของส่วนของเส้นทแยงมุมสามารถพิสูจน์ได้จากความเท่าเทียมกันของรูปสามเหลี่ยมเอโอบีและ ซี.โอ.ดี.. การใช้คุณสมบัติเดิมของสี่เหลี่ยมด้านขนาน จะทำให้เดาได้ว่าด้านทั้งสองเท่ากันเอบีและ ซีดี. จากนั้นพวกเขาก็เข้าใจว่าจำเป็นต้องหามุมที่เท่ากันและพิสูจน์ความเท่าเทียมกันของมุมที่อยู่ติดกันโดยใช้คุณสมบัติของเส้นคู่ขนาน ฝ่ายที่เท่าเทียมกันมุม ขั้นตอนเหล่านี้จะแสดงเป็นภาพบนสไลด์ ความจริงของทฤษฎีบทตามมาจากความเท่าเทียมกันของสามเหลี่ยม - นักเรียนพูดและการแสดงภาพที่สอดคล้องกันปรากฏบนสไลด์

(สไลด์ 6)

ครูกำหนดคุณสมบัติที่สามของสี่เหลี่ยมด้านขนาน ขึ้นอยู่กับเวลาที่เหลืออยู่จนจบบทเรียน ครูสามารถให้โอกาสนักเรียนพิสูจน์คุณสมบัตินี้ได้อย่างอิสระ หรือจำกัดตัวเองอยู่ในสูตร และปล่อยให้นักเรียนพิสูจน์เอง การบ้าน. การพิสูจน์อาจขึ้นอยู่กับผลรวมของมุมของรูปหลายเหลี่ยมที่ถูกจารึกไว้ ซึ่งถูกทำซ้ำในตอนต้นของบทเรียน หรือจากผลรวมของมุมด้านเดียวภายในของเส้นคู่ขนานสองเส้นค.ศและ บี.ซี.และซีแคนต์ เป็นต้นเอบี.

4. การยึดวัสดุ

ในขั้นตอนนี้ นักเรียนใช้ทฤษฎีบทที่เรียนมาก่อนหน้านี้เพื่อแก้ปัญหา นักเรียนเลือกแนวคิดในการแก้ปัญหาอย่างอิสระ เพราะ ตัวเลือกที่เป็นไปได้มีการออกแบบมากมายและทั้งหมดขึ้นอยู่กับว่านักเรียนจะมองหาวิธีแก้ไขปัญหาอย่างไร ไม่มีการแสดงภาพวิธีแก้ปัญหา และนักเรียนจะวาดแต่ละขั้นตอนของการแก้ปัญหาบนกระดานแยกกันโดยอิสระ บันทึกโซลูชันลงในสมุดบันทึก

(สไลด์ 7)

เงื่อนไขของงานปรากฏขึ้น ครูเสนอแนะให้กำหนด “การให้” ตามเงื่อนไข หลังจากนักเรียนจดข้อความสั้นๆ เกี่ยวกับเงื่อนไขอย่างถูกต้องแล้ว “ให้ไว้” จะปรากฏบนกระดาน กระบวนการแก้ไขปัญหาอาจมีลักษณะดังนี้:

ลองวาดส่วนสูง BH (เห็นภาพ)

สามเหลี่ยม AHB เป็นสามเหลี่ยมมุมฉาก มุม ก เท่ากับมุม C และเท่ากับ 30 0 (ตามคุณสมบัติของมุมตรงข้ามในรูปสี่เหลี่ยมด้านขนาน) 2BH =AB (โดยคุณสมบัติของขาที่วางตรงข้ามมุม 30 0 ในรูปสามเหลี่ยมมุมฉาก) ดังนั้น AB = 13 ซม.

AB = CD, BC = AD (ตามคุณสมบัติของด้านตรงข้ามในรูปสี่เหลี่ยมด้านขนาน) ดังนั้น AB = CD = 13 ซม. เนื่องจากเส้นรอบรูปของสี่เหลี่ยมด้านขนานคือ 50 ซม. ดังนั้น BC = AD = (50 – 26): 2 = 12 ซม.

คำตอบ: AB = CD = 13 ซม. BC = AD = 12 ซม.

(สไลด์ 8)

เงื่อนไขของงานปรากฏขึ้น ครูเสนอแนะให้กำหนด “การให้” ตามเงื่อนไข จากนั้นข้อความ “ให้” จะปรากฏบนหน้าจอ ใช้เส้นสีแดงเพื่อเน้นรูปสี่เหลี่ยมขนมเปียกปูน ซึ่งคุณต้องพิสูจน์ว่าเป็นสี่เหลี่ยมด้านขนาน กระบวนการแก้ไขปัญหาอาจมีลักษณะดังนี้:

เพราะ BK และ MD ตั้งฉากกับเส้นตรงหนึ่งเส้น จากนั้นเส้น BK และ MD จะขนานกัน

จากมุมที่อยู่ติดกัน จะแสดงให้เห็นว่าผลรวมของมุมด้านเดียวภายในที่เส้นตรง BM และ KD และเส้นตัด MD เท่ากับ 180 0 ดังนั้นเส้นเหล่านี้จึงขนานกัน

เนื่องจากรูปสี่เหลี่ยม BMDK มีด้านตรงข้ามขนานกันเป็นคู่ ดังนั้นรูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นรูปสี่เหลี่ยมด้านขนาน

5. จบบทเรียน พฤติกรรมของผลลัพธ์

(สไลด์ 8)

คำถามในหัวข้อใหม่จะปรากฏบนสไลด์ซึ่งนักเรียนตอบ

แนวคิดเรื่องสี่เหลี่ยมด้านขนาน

คำจำกัดความ 1

สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมที่มีด้านตรงข้ามขนานกัน (รูปที่ 1)

ภาพที่ 1.

สี่เหลี่ยมด้านขนานมีคุณสมบัติหลักสองประการ ลองพิจารณาโดยไม่มีข้อพิสูจน์

คุณสมบัติ 1: ด้านตรงข้ามและมุมของสี่เหลี่ยมด้านขนานจะเท่ากันตามลำดับ

คุณสมบัติ 2: เส้นทแยงมุมที่วาดในรูปสี่เหลี่ยมด้านขนานจะถูกแบ่งครึ่งตามจุดตัด

สัญญาณของรูปสี่เหลี่ยมด้านขนาน

ลองพิจารณาคุณลักษณะสามประการของสี่เหลี่ยมด้านขนานแล้วนำเสนอในรูปแบบของทฤษฎีบท

ทฤษฎีบท 1

ถ้าด้านสองด้านของรูปสี่เหลี่ยมด้านขนานเท่ากันและขนานกัน รูปสี่เหลี่ยมด้านนี้ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์.

ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ โดยที่ $AB||CD$ และ $AB=CD$ ให้เราวาดเส้นทแยงมุม $AC$ ในนั้น (รูปที่ 2)

รูปที่ 2.

พิจารณาเส้นคู่ขนาน $AB$ และ $CD$ และเส้นตัดกัน $AC$ แล้ว

\[\มุม CAB=\มุม DCA\]

เหมือนมุมที่ไขว้กัน

ตามเกณฑ์ $I$ ของความเท่าเทียมกันของรูปสามเหลี่ยม

เนื่องจาก $AC$ เป็นด้านร่วม และ $AB=CD$ ตามเงื่อนไข วิธี

\[\มุม DAC=\มุม ACB\]

พิจารณาเส้นตรง $AD$ และ $CB$ และเส้นตัดขวาง $AC$ โดยความเท่ากันสุดท้ายของมุมนอนเราจะได้ $AD||CB$.) ดังนั้น ตามคำจำกัดความ $1$ รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน

ทฤษฎีบทได้รับการพิสูจน์แล้ว

ทฤษฎีบท 2

ถ้าด้านตรงข้ามของรูปสี่เหลี่ยมขนมเปียกปูนเท่ากัน แสดงว่าเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์.

ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ โดยที่ $AD=BC$ และ $AB=CD$ ให้เราวาดเส้นทแยงมุม $AC$ ไว้ข้างใน (รูปที่ 3)

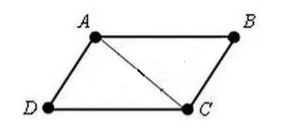
รูปที่ 3.

เนื่องจาก $AD=BC$, $AB=CD$ และ $AC$ เป็นด้านร่วม ดังนั้นตามเกณฑ์ $III$ สำหรับความเท่ากันของรูปสามเหลี่ยม

\[\สามเหลี่ยม DAC=\สามเหลี่ยม ACB\]

\[\มุม DAC=\มุม ACB\]

ลองพิจารณาเส้น $AD$ และ $CB$ และเส้นตัดขวาง $AC$ ของเส้นเหล่านั้น โดยความเสมอภาคสุดท้ายข้ามมุมโกหก เราจะได้ $AD||CB$ ดังนั้น ตามคำนิยาม $1$ รูปสี่เหลี่ยมด้านขนานนี้จึงเป็นสี่เหลี่ยมด้านขนาน

\[\มุม DCA=\มุม CAB\]

ลองพิจารณาเส้น $AB$ และ $CD$ และเส้นตัดขวาง $AC$ ของเส้นเหล่านั้น โดยความเสมอภาคสุดท้ายข้ามมุมนอน เราจะได้ $AB||CD$ ดังนั้น ตามคำจำกัดความที่ 1 รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน

ทฤษฎีบทได้รับการพิสูจน์แล้ว

ทฤษฎีบท 3

หากเส้นทแยงมุมที่วาดเป็นรูปสี่เหลี่ยมขนมเปียกปูนถูกแบ่งออกเป็นสองส่วนเท่าๆ กันด้วยจุดตัดกัน รูปสี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์.

ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ ให้เราวาดเส้นทแยงมุม $AC$ และ $BD$ ลงไป ปล่อยให้พวกมันตัดกันที่จุด $O$ (รูปที่ 4)

รูปที่ 4.

เนื่องจากตามเงื่อนไข $BO=OD,\ AO=OC$ และมุม $\angle COB=\angle DOA$ นั้นเป็นแนวตั้ง ดังนั้น ด้วยเกณฑ์ $I$ สำหรับความเท่าเทียมกันของรูปสามเหลี่ยม

\[\สามเหลี่ยม BOC=\สามเหลี่ยม AOD\]

\[\มุม DBC=\มุม BDA\]

พิจารณาเส้น $BC$ และ $AD$ และเส้นตัดขวาง $BD$ โดยความเสมอภาคสุดท้ายของมุมนอนเราจะได้ $BC||AD$ $BC=AD$ เช่นกัน ดังนั้น ตามทฤษฎีบท $1$ รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน

สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมขนมเปียกปูนที่มีด้านตรงข้ามขนานกันเป็นคู่ คำจำกัดความนี้เพียงพอแล้ว เนื่องจากคุณสมบัติที่เหลือของสี่เหลี่ยมด้านขนานตามมาและได้รับการพิสูจน์ในรูปแบบของทฤษฎีบท

คุณสมบัติหลักของสี่เหลี่ยมด้านขนานคือ:

สี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนนูน
สี่เหลี่ยมด้านขนานมีด้านตรงข้ามที่เท่ากันเป็นคู่
ในสี่เหลี่ยมด้านขนาน มุมตรงข้ามจะเท่ากันเป็นคู่
เส้นทแยงมุมของสี่เหลี่ยมด้านขนานจะถูกแบ่งครึ่งตามจุดตัด

สี่เหลี่ยมด้านขนาน - รูปสี่เหลี่ยมด้านขนานนูน

ก่อนอื่นให้เราพิสูจน์ทฤษฎีบทนั้นก่อน สี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนนูน. รูปหลายเหลี่ยมจะนูนออกมาหากด้านใดด้านหนึ่งของรูปหลายเหลี่ยมยื่นออกไปเป็นเส้นตรง ด้านอื่นๆ ทั้งหมดของรูปหลายเหลี่ยมก็จะอยู่บนด้านเดียวกันของเส้นตรงนี้

ให้รูปสี่เหลี่ยมด้านขนาน ABCD โดยที่ AB เป็นด้านตรงข้ามของ CD และ BC เป็นด้านตรงข้ามของ AD จากนิยามของสี่เหลี่ยมด้านขนาน จะได้ว่า AB || ซีดี, ก่อนคริสต์ศักราช || อ.

ส่วนขนานไม่มีจุดร่วมและไม่ตัดกัน ซึ่งหมายความว่า CD อยู่ด้านหนึ่งของ AB เนื่องจากเส้น BC เชื่อมต่อจุด B ของเส้น AB กับจุด C ของเส้น CD ส่วน และเส้น AD เชื่อมต่อจุด AB และ CD อื่นๆ เส้น BC และ AD จึงอยู่บนด้านเดียวกันของเส้น AB โดยที่ CD อยู่ ดังนั้นทั้งสามด้าน - CD, BC, AD - นอนอยู่บนด้านเดียวกันของ AB

ในทำนองเดียวกัน มีการพิสูจน์ว่าเมื่อสัมพันธ์กับด้านอื่นๆ ของสี่เหลี่ยมด้านขนาน อีกสามด้านจะอยู่ด้านเดียวกัน

ด้านตรงข้ามและมุมเท่ากัน

คุณสมบัติอย่างหนึ่งของสี่เหลี่ยมด้านขนานก็คือ ในสี่เหลี่ยมด้านขนาน ด้านตรงข้ามและมุมตรงข้ามจะเท่ากันเป็นคู่. ตัวอย่างเช่น หากกำหนดสี่เหลี่ยมด้านขนาน ABCD จะมี AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D ทฤษฎีบทนี้ได้รับการพิสูจน์ดังนี้

สี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูน ซึ่งหมายความว่ามีเส้นทแยงมุมสองเส้น เนื่องจากรูปสี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนนูน รูปใดรูปหนึ่งจึงแบ่งออกเป็นสามเหลี่ยมสองรูป ในสี่เหลี่ยมด้านขนาน ABCD ให้พิจารณาสามเหลี่ยม ABC และ ADC ที่ได้จากการวาดเส้นทแยงมุม AC

สามเหลี่ยมเหล่านี้มีด้านเดียวเหมือนกัน - AC มุม BCA เท่ากับมุม CAD เช่นเดียวกับแนวตั้งเมื่อ BC และ AD ขนานกัน มุม BAC และ ACD จะเท่ากับมุมแนวตั้งเมื่อ AB และ CD ขนานกัน ดังนั้น ∆ABC = ∆ADC ที่มุมสองมุมและด้านระหว่างมุมทั้งสอง

ในรูปสามเหลี่ยมเหล่านี้ ด้าน AB ตรงกับด้าน CD และด้าน BC ตรงกับ AD ดังนั้น AB = CD และ BC = AD

มุม B สอดคล้องกับมุม D เช่น ∠B = ∠D มุม A ของสี่เหลี่ยมด้านขนานคือผลรวมของสองมุม - ∠BAC และ ∠CAD มุม C เท่ากับ ∠BCA และ ∠ACD เนื่องจากมุมคู่มีค่าเท่ากัน ดังนั้น ∠A = ∠C

ดังนั้นจึงพิสูจน์ได้ว่าในรูปสี่เหลี่ยมด้านขนานด้านตรงข้ามและมุมเท่ากัน

เส้นทแยงมุมแบ่งออกเป็นสองส่วน

เนื่องจากสี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนนูน จึงมีเส้นทแยงมุมสองเส้นและตัดกัน ให้รูปสี่เหลี่ยมด้านขนาน ABCD เส้นทแยงมุม AC และ BD ตัดกันที่จุด E พิจารณาสามเหลี่ยม ABE และ CDE ที่เกิดขึ้นจากพวกมัน

สามเหลี่ยมเหล่านี้มีด้าน AB และ CD เท่ากับด้านตรงข้ามของสี่เหลี่ยมด้านขนาน มุม ABE เท่ากับมุม CDE เมื่อวางขวางโดยมีเส้นขนาน AB และ CD ด้วยเหตุผลเดียวกัน ∠BAE = ∠DCE ซึ่งหมายความว่า ∆ABE = ∆CDE ที่มุมสองมุมและด้านระหว่างมุมทั้งสอง

คุณยังสังเกตได้ว่ามุม AEB และ CED เป็นมุมตั้งฉากและมีค่าเท่ากันด้วย

เนื่องจากสามเหลี่ยม ABE และ CDE เท่ากัน ดังนั้น องค์ประกอบที่ตรงกันทั้งหมดจึงเท่ากัน ด้าน AE ของสามเหลี่ยมแรกตรงกับด้าน CE ของสามเหลี่ยมที่สอง ซึ่งหมายถึง AE = CE ในทำนองเดียวกัน BE = DE ส่วนเท่ากันแต่ละคู่ประกอบเป็นเส้นทแยงมุมของสี่เหลี่ยมด้านขนาน จึงพิสูจน์ได้ว่า เส้นทแยงมุมของสี่เหลี่ยมด้านขนานจะถูกแบ่งออกเป็นสองส่วนตามจุดตัด.

ในบทเรียนวันนี้ เราจะทบทวนคุณสมบัติพื้นฐานของรูปสี่เหลี่ยมด้านขนาน จากนั้นเราจะให้ความสนใจกับการพิจารณาคุณสมบัติสองประการแรกของรูปสี่เหลี่ยมด้านขนานแล้วพิสูจน์มัน ในระหว่างการพิสูจน์ ให้เรานึกถึงการใช้การทดสอบความเท่าเทียมกันของสามเหลี่ยม ซึ่งเราศึกษาเมื่อปีที่แล้วและทำซ้ำในบทเรียนแรก ในตอนท้าย จะมีการยกตัวอย่างเกี่ยวกับการใช้คุณลักษณะที่ศึกษาของรูปสี่เหลี่ยมด้านขนาน

หัวข้อ: รูปสี่เหลี่ยม

บทเรียน: สัญญาณของสี่เหลี่ยมด้านขนาน

เริ่มต้นด้วยการนึกถึงคำจำกัดความของสี่เหลี่ยมด้านขนาน

คำนิยาม. สี่เหลี่ยมด้านขนาน- รูปสี่เหลี่ยมขนมเปียกปูนที่ด้านตรงข้ามทุกสองด้านขนานกัน (ดูรูปที่ 1)

ข้าว. 1. สี่เหลี่ยมด้านขนาน

มาจำกัน คุณสมบัติพื้นฐานของรูปสี่เหลี่ยมด้านขนาน:

เพื่อที่จะสามารถใช้คุณสมบัติทั้งหมดนี้ได้ คุณต้องแน่ใจว่ารูปที่ต้องการนั้นเป็นสี่เหลี่ยมด้านขนาน ในการทำเช่นนี้ คุณจำเป็นต้องรู้ข้อเท็จจริงต่างๆ เช่น คุณลักษณะของสี่เหลี่ยมด้านขนาน เราจะพิจารณาสองคนแรกในวันนี้

ทฤษฎีบท. เครื่องหมายแรกของรูปสี่เหลี่ยมด้านขนานถ้าด้านตรงข้ามสองด้านของรูปสี่เหลี่ยมขนมเปียกปูนเท่ากันและขนานกัน รูปสี่เหลี่ยมนี้จะเท่ากับ สี่เหลี่ยมด้านขนาน. .

ข้าว. 2. เครื่องหมายแรกของรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์. ลองวาดเส้นทแยงมุมในรูปสี่เหลี่ยมขนมเปียกปูน (ดูรูปที่ 2) โดยแบ่งออกเป็นสามเหลี่ยมสองรูป ลองเขียนสิ่งที่เรารู้เกี่ยวกับสามเหลี่ยมเหล่านี้:

ตามเกณฑ์แรกของความเท่าเทียมกันของรูปสามเหลี่ยม

จากความเท่าเทียมกันของรูปสามเหลี่ยมที่ระบุ จะเป็นไปตามนั้นโดยอาศัยความขนานของเส้นเมื่อตัดกับเส้นตัด เรามีสิ่งนั้น:

พิสูจน์แล้ว

ทฤษฎีบท. เครื่องหมายที่สองของสี่เหลี่ยมด้านขนานถ้าในรูปสี่เหลี่ยมด้านตรงข้ามทุกสองด้านเท่ากัน รูปสี่เหลี่ยมนี้จะเท่ากับ สี่เหลี่ยมด้านขนาน. .

ข้าว. 3. เครื่องหมายที่สองของสี่เหลี่ยมด้านขนาน

การพิสูจน์. ลองวาดเส้นทแยงมุมในรูปสี่เหลี่ยมจัตุรัส (ดูรูปที่ 3) โดยแบ่งออกเป็นสามเหลี่ยมสองรูป ให้เราเขียนสิ่งที่เรารู้เกี่ยวกับสามเหลี่ยมเหล่านี้ตามการกำหนดทฤษฎีบท:

ตามเกณฑ์ที่สามสำหรับความเท่าเทียมกันของรูปสามเหลี่ยม