จำนวนในช่วงเวลาเป็นจำนวนตรรกยะหรือจำนวนอตรรกยะ จำนวนอตรรกยะหมายถึงอะไร?

เนื้อหาในบทความนี้ให้ข้อมูลเบื้องต้นเกี่ยวกับ ตัวเลขอตรรกยะ. ก่อนอื่นเราจะให้คำจำกัดความของจำนวนอตรรกยะและอธิบายก่อน ด้านล่างนี้เราจะยกตัวอย่างจำนวนอตรรกยะ สุดท้ายนี้ เรามาดูวิธีการบางอย่างในการหาว่าจำนวนที่ระบุนั้นไม่มีเหตุผลหรือไม่

การนำทางหน้า

ความหมายและตัวอย่างจำนวนอตรรกยะ

เมื่อศึกษาทศนิยม เราจะพิจารณาทศนิยมแบบไม่สิ้นสุดเป็นช่วงอนันต์แยกกัน เศษส่วนดังกล่าวเกิดขึ้นเมื่อวัดความยาวทศนิยมของส่วนที่ไม่สามารถเทียบเคียงกับส่วนของหน่วยได้ นอกจากนี้เรายังตั้งข้อสังเกตอีกว่าเศษส่วนทศนิยมที่ไม่ใช่คาบไม่จำกัดไม่สามารถแปลงเป็นเศษส่วนสามัญได้ (ดูการแปลงเศษส่วนสามัญเป็นทศนิยมและในทางกลับกัน) ดังนั้น ตัวเลขเหล่านี้จึงไม่ใช่จำนวนตรรกยะ แต่เป็นตัวแทนของสิ่งที่เรียกว่าจำนวนอตรรกยะ

เราก็เลยมา. คำจำกัดความของจำนวนอตรรกยะ.

คำนิยาม.

ตัวเลขที่แสดงถึงเศษส่วนทศนิยมที่ไม่ใช่คาบเป็นอนันต์ในรูปแบบทศนิยมเรียกว่า ตัวเลขอตรรกยะ.

คำจำกัดความที่เปล่งออกมาช่วยให้เราสามารถให้ ตัวอย่างของจำนวนอตรรกยะ. ตัวอย่างเช่น เศษส่วนทศนิยมแบบไม่เป็นงวด 4.10110011100011110000... (จำนวนหลักและศูนย์เพิ่มขึ้นครั้งละหนึ่ง) ถือเป็นจำนวนอตรรกยะ ลองยกตัวอย่างอีกตัวอย่างหนึ่งของจำนวนอตรรกยะ: −22.353335333335... (จำนวนสามที่แยกแปดออกจะเพิ่มขึ้นทีละสองในแต่ละครั้ง)

ควรสังเกตว่าจำนวนอตรรกยะนั้นค่อนข้างหายากในรูปแบบของเศษส่วนทศนิยมที่ไม่มีคาบไม่สิ้นสุด มักจะพบในรูปแบบ ฯลฯ เช่นเดียวกับในรูปแบบของตัวอักษรที่ป้อนเป็นพิเศษ ที่สุด ตัวอย่างที่มีชื่อเสียงจำนวนอตรรกยะในรูปแบบนี้คือรากที่สองทางคณิตศาสตร์ของสอง จำนวน “pi” π=3.141592... จำนวน e=2.718281... และจำนวนทอง

จำนวนอตรรกยะสามารถกำหนดได้ในรูปของจำนวนจริง ซึ่งรวมจำนวนตรรกยะและจำนวนอตรรกยะเข้าด้วยกัน

คำนิยาม.

ตัวเลขอตรรกยะเป็นจำนวนจริงที่ไม่ใช่จำนวนตรรกยะ

ตัวเลขนี้ไม่มีเหตุผลใช่ไหม?

เมื่อตัวเลขไม่ได้ถูกกำหนดให้เป็นเศษส่วนทศนิยม แต่เป็นราก ลอการิทึม ฯลฯ การตอบคำถามว่าไม่มีเหตุผลนั้นค่อนข้างยากในหลายกรณี

ไม่ต้องสงสัยเลยว่าเมื่อตอบคำถามที่ถูกวางไว้จะมีประโยชน์มากที่จะรู้ว่าตัวเลขใดที่ไม่ลงตัว จากคำจำกัดความของจำนวนอตรรกยะ จะได้ว่าจำนวนอตรรกยะไม่ใช่จำนวนตรรกยะ ดังนั้น จำนวนอตรรกยะจึงไม่ใช่:

• เศษส่วนทศนิยมเป็นงวดที่มีขอบเขตจำกัดและอนันต์

นอกจากนี้ องค์ประกอบของจำนวนตรรกยะใดๆ ที่เชื่อมต่อกันด้วยเครื่องหมายของการดำเนินการทางคณิตศาสตร์ (+, −, ·, :) ก็ไม่ใช่จำนวนอตรรกยะ เนื่องจากผลรวม ผลต่าง ผลคูณ และผลหารของจำนวนตรรกยะสองตัวนั้นเป็นจำนวนตรรกยะ เช่น ค่าของนิพจน์และเป็นจำนวนตรรกยะ ในที่นี้เราทราบว่าหากนิพจน์ดังกล่าวมีจำนวนอตรรกยะตัวเดียวในหมู่จำนวนตรรกยะ ค่าของนิพจน์ทั้งหมดจะเป็นจำนวนอตรรกยะ ตัวอย่างเช่น ในนิพจน์ จำนวนเป็นจำนวนตรรกยะ และจำนวนที่เหลือเป็นจำนวนตรรกยะ ดังนั้นจึงเป็นจำนวนอตรรกยะ ถ้าเป็นจำนวนตรรกยะ ความสมเหตุสมผลของจำนวนก็จะตามมา แต่จำนวนนั้นไม่เป็นตรรกยะ

หากนิพจน์ที่ระบุตัวเลขประกอบด้วยจำนวนอตรรกยะ เครื่องหมายราก ลอการิทึม ฟังก์ชันตรีโกณมิติ, ตัวเลข π, e ฯลฯ จากนั้นจะต้องพิสูจน์ความไร้เหตุผลหรือเหตุผลของจำนวนที่กำหนดในแต่ละกรณีโดยเฉพาะ อย่างไรก็ตาม มีผลลัพธ์จำนวนหนึ่งที่สามารถนำมาใช้ได้ เรามาแสดงรายการหลักกัน

ได้รับการพิสูจน์แล้วว่ารากที่ k ของจำนวนเต็มเป็นจำนวนตรรกยะก็ต่อเมื่อตัวเลขที่อยู่ใต้รากนั้นเป็นกำลัง k ของจำนวนเต็มอีกจำนวนหนึ่ง ในกรณีอื่น รากดังกล่าวระบุจำนวนอตรรกยะ ตัวอย่างเช่น ตัวเลข และ เป็นจำนวนอตรรกยะ เนื่องจากไม่มีจำนวนเต็มที่มีกำลังสองเป็น 7 และไม่มีจำนวนเต็มซึ่งการบวกยกกำลังที่ 5 จะให้เลข 15 และตัวเลขนั้นไม่เป็นจำนวนตรรกยะ เนื่องจาก และ .

สำหรับลอการิทึม บางครั้งเป็นไปได้ที่จะพิสูจน์ความไร้เหตุผลโดยใช้วิธีขัดแย้ง ตามตัวอย่าง ลองพิสูจน์ว่าบันทึก 2 3 เป็นจำนวนอตรรกยะ

สมมติว่าบันทึก 2 3 เป็นจำนวนตรรกยะและไม่ใช่จำนวนอตรรกยะ กล่าวคือ สามารถแสดงเป็น เศษส่วนทั่วไปม./น. และให้เราเขียนห่วงโซ่แห่งความเท่าเทียมกันดังต่อไปนี้: . ความเท่าเทียมกันครั้งสุดท้ายเป็นไปไม่ได้เนื่องจากอยู่ทางด้านซ้าย เลขคี่และทางด้านขวา – เท่ากัน ดังนั้นเราจึงเกิดข้อขัดแย้ง ซึ่งหมายความว่าสมมติฐานของเราไม่ถูกต้อง และพิสูจน์ว่าบันทึก 2 3 เป็นจำนวนอตรรกยะ

โปรดทราบว่า lna สำหรับ a ที่เป็นจำนวนตรรกยะบวกและไม่เป็นหนึ่งใดๆ จะเป็นจำนวนอตรรกยะ ตัวอย่างเช่น และ เป็นจำนวนอตรรกยะ

นอกจากนี้ยังพิสูจน์ได้ว่าจำนวน e a สำหรับจำนวนตรรกยะที่ไม่เป็นศูนย์ a ใดๆ นั้นเป็นจำนวนอตรรกยะ และจำนวน π z สำหรับจำนวนเต็มที่ไม่ใช่ศูนย์ใดๆ z นั้นเป็นจำนวนอตรรกยะ เช่น ตัวเลขไม่ลงตัว

จำนวนอตรรกยะก็เป็นวิชาตรีโกณมิติเช่นกัน ทำหน้าที่บาป, cos , tg และ ctg สำหรับค่าเหตุผลและไม่เป็นศูนย์ใดๆ ของอาร์กิวเมนต์ ตัวอย่างเช่น sin1 , tan(−4) , cos5,7 เป็นจำนวนอตรรกยะ

ยังมีผลลัพธ์ที่พิสูจน์แล้วอื่นๆ แต่เราจะจำกัดตัวเองไว้เฉพาะผลลัพธ์ที่ระบุไว้แล้ว ก็ควรจะกล่าวด้วยว่าเมื่อพิสูจน์ผลลัพธ์ข้างต้นทฤษฎีที่เกี่ยวข้องด้วย ตัวเลขพีชคณิตและ ตัวเลขเหนือธรรมชาติ.

โดยสรุป เราทราบว่าเราไม่ควรด่วนสรุปเกี่ยวกับความไร้เหตุผลของตัวเลขที่กำหนด ตัวอย่างเช่น เห็นได้ชัดว่าจำนวนอตรรกยะถึงระดับที่ไม่ลงตัวนั้นเป็นจำนวนอตรรกยะ อย่างไรก็ตาม นี่ไม่ใช่กรณีเสมอไป เพื่อยืนยันข้อเท็จจริงดังกล่าว เราขอนำเสนอปริญญา เป็นที่ทราบกันว่า - เป็นจำนวนอตรรกยะ และได้รับการพิสูจน์แล้วว่า - เป็นจำนวนอตรรกยะ แต่เป็นจำนวนตรรกยะ คุณยังสามารถยกตัวอย่างจำนวนอตรรกยะ ผลรวม ผลต่าง ผลคูณ และผลหารที่เป็นจำนวนตรรกยะได้ ยิ่งไปกว่านั้น ความสมเหตุสมผลหรือความไม่ลงตัวของตัวเลข π+e, π−e, π·e, π π, π e และอื่นๆ อีกมากมายยังไม่ได้รับการพิสูจน์

บรรณานุกรม.

• คณิตศาสตร์.ชั้นประถมศึกษาปีที่ 6: การศึกษา เพื่อการศึกษาทั่วไป สถาบัน / [น. ใช่ Vilenkin และคนอื่น ๆ] - ฉบับที่ 22, ว. - อ.: Mnemosyne, 2551. - 288 หน้า: ป่วย. ไอ 978-5-346-00897-2.
• พีชคณิต:หนังสือเรียน สำหรับเกรด 8 การศึกษาทั่วไป สถาบัน / [ย. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; แก้ไขโดย เอส.เอ. เทลยาคอฟสกี้ - ฉบับที่ 16 - อ.: การศึกษา, 2551. - 271 น. : ป่วย. - ไอ 978-5-09-019243-9.
• Gusev V.A., Mordkovich A.G.คณิตศาสตร์ (คู่มือสำหรับผู้เข้าโรงเรียนเทคนิค) พรบ. เบี้ยเลี้ยง.- ม.; สูงกว่า โรงเรียน พ.ศ. 2527-351 น. ป่วย

การทำความเข้าใจตัวเลข โดยเฉพาะจำนวนธรรมชาติ เป็นหนึ่งใน "ทักษะ" ทางคณิตศาสตร์ที่เก่าแก่ที่สุด อารยธรรมหลายแห่ง แม้แต่อารยธรรมสมัยใหม่ ก็ได้ให้คุณสมบัติลึกลับบางอย่างมาจากตัวเลข เนื่องจากมีความสำคัญอย่างมากในการอธิบายธรรมชาติ แม้ว่า วิทยาศาสตร์สมัยใหม่และคณิตศาสตร์ไม่ได้ยืนยันคุณสมบัติ "มหัศจรรย์" เหล่านี้ ความสำคัญของทฤษฎีจำนวนก็ไม่อาจปฏิเสธได้

ในอดีต จำนวนธรรมชาติจำนวนหนึ่งปรากฏขึ้นก่อน จากนั้นจึงบวกเศษส่วนอย่างรวดเร็วและจำนวนอตรรกยะบวกเข้าไป จำนวนศูนย์และจำนวนลบถูกนำมาใช้หลังจากเซตย่อยของเซตของจำนวนจริง ชุดสุดท้ายชุด จำนวนเชิงซ้อนปรากฏเฉพาะเมื่อมีการพัฒนาทางวิทยาศาสตร์สมัยใหม่เท่านั้น

ในคณิตศาสตร์สมัยใหม่ ตัวเลขไม่ได้ถูกนำมาใช้ตามลำดับประวัติศาสตร์ แม้ว่าจะค่อนข้างใกล้เคียงกันก็ตาม

จำนวนธรรมชาติ $\mathbb(N)$

เซตของจำนวนธรรมชาติมักแสดงเป็น $\mathbb(N)=\lbrace 1,2,3,4... \rbrace $ และมักจะเติมด้วยศูนย์เพื่อแสดงถึง $\mathbb(N)_0$

$\mathbb(N)$ กำหนดการดำเนินการของการบวก (+) และการคูณ ($\cdot$) ด้วยคุณสมบัติต่อไปนี้สำหรับ $a,b,c\in \mathbb(N)$ ใดๆ:

1. $a+b\in \mathbb(N)$, $a\cdot b \in \mathbb(N)$ เซต $\mathbb(N)$ ถูกปิดภายใต้การดำเนินการของการบวกและการคูณ
2. $a+b=b+a$, $a\cdot b=b\cdot a$ สับเปลี่ยน
3. $(a+b)+c=a+(b+c)$, $(a\cdot b)\cdot c=a\cdot (b\cdot c)$ การเชื่อมโยง
4. $a\cdot (b+c)=a\cdot b+a\cdot c$ การกระจายตัว
5. $a\cdot 1=a$ เป็นองค์ประกอบที่เป็นกลางสำหรับการคูณ

เนื่องจากชุด $\mathbb(N)$ มีองค์ประกอบที่เป็นกลางสำหรับการคูณ แต่ไม่ใช่สำหรับการบวก การบวกศูนย์เข้ากับชุดนี้จึงทำให้แน่ใจได้ว่าจะมีองค์ประกอบที่เป็นกลางสำหรับการบวก

นอกเหนือจากการดำเนินการทั้งสองนี้แล้ว ความสัมพันธ์ "น้อยกว่า" ($

1. $a b$ การผ่าตัดไตรโคโตมี
2. ถ้า $a\leq b$ และ $b\leq a$ แล้ว $a=b$ ความไม่สมมาตร
3. ถ้า $a\leq b$ และ $b\leq c$ แล้ว $a\leq c$ จะเป็นสกรรมกริยา
4. ถ้า $a\leq b$ แล้ว $a+c\leq b+c$
5. ถ้า $a\leq b$ แล้ว $a\cdot c\leq b\cdot c$

จำนวนเต็ม $\mathbb(Z)$

ตัวอย่างของจำนวนเต็ม:
$1, -20, -100, 30, -40, 120...$

การแก้สมการ $a+x=b$ โดยที่ $a$ และ $b$ เป็นที่รู้จักว่าเป็นจำนวนธรรมชาติ และ $x$ เป็นจำนวนธรรมชาติที่ไม่รู้จัก จำเป็นต้องมีการดำเนินการใหม่ - การลบ (-) หากมีจำนวนธรรมชาติ $x$ ที่เป็นไปตามสมการนี้ แล้ว $x=b-a$ อย่างไรก็ตาม สมการเฉพาะนี้ไม่จำเป็นต้องมีคำตอบบนเซต $\mathbb(N)$ ดังนั้นการพิจารณาเชิงปฏิบัติจึงต้องขยายชุดของจำนวนธรรมชาติเพื่อรวมคำตอบของสมการนั้นด้วย สิ่งนี้นำไปสู่การแนะนำชุดจำนวนเต็ม: $\mathbb(Z)=\lbrace 0,1,-1,2,-2,3,-3...\rbrace$

เนื่องจาก $\mathbb(N)\subset \mathbb(Z)$ จึงสมเหตุสมผลที่จะถือว่าการดำเนินการที่แนะนำก่อนหน้านี้ $+$ และ $\cdot$ และความสัมพันธ์ $ 1 $0+a=a+0=a$ มีองค์ประกอบที่เป็นกลางสำหรับการเพิ่มเติม
2. $a+(-a)=(-a)+a=0$ มีตัวเลขตรงข้าม $-a$ สำหรับ $a$

คุณสมบัติ 5.:
5. ถ้า $0\leq a$ และ $0\leq b$ แล้ว $0\leq a\cdot b$

เซต $\mathbb(Z)$ จะถูกปิดภายใต้การดำเนินการลบเช่นกัน นั่นคือ $(\forall a,b\in \mathbb(Z))(a-b\in \mathbb(Z))$

จำนวนตรรกยะ $\mathbb(Q)$

ตัวอย่างของจำนวนตรรกยะ:
$\frac(1)(2), \frac(4)(7), -\frac(5)(8), \frac(10)(20)...$

ตอนนี้ ให้พิจารณาสมการในรูปแบบ $a\cdot x=b$ โดยที่ $a$ และ $b$ เป็นที่รู้จักว่าเป็นจำนวนเต็ม และ $x$ เป็นที่รู้จัก เพื่อให้วิธีแก้ปัญหาเป็นไปได้ จำเป็นต้องเริ่มดำเนินการหาร ($:$) และวิธีแก้ปัญหาจะอยู่ในรูปแบบ $x=b:a$ นั่นคือ $x=\frac(b)(a)$ . ปัญหาเกิดขึ้นอีกครั้งว่า $x$ ไม่ได้เป็นของ $\mathbb(Z)$ เสมอไป ดังนั้นจึงจำเป็นต้องขยายชุดของจำนวนเต็ม นี่เป็นการแนะนำชุดของจำนวนตรรกยะ $\mathbb(Q)$ ที่มีองค์ประกอบ $\frac(p)(q)$ โดยที่ $p\in \mathbb(Z)$ และ $q\in \mathbb(N)$ เซต $\mathbb(Z)$ เป็นเซตย่อยที่แต่ละสมาชิก $q=1$ ดังนั้น $\mathbb(Z)\subset \mathbb(Q)$ และการดำเนินการของการบวกและการคูณจะขยายไปยังเซตนี้ตาม กฎต่อไปนี้ ซึ่งรักษาคุณสมบัติข้างต้นทั้งหมดไว้ในชุด $\mathbb(Q)$:
$\frac(p_1)(q_1)+\frac(p_2)(q_2)=\frac(p_1\cdot q_2+p_2\cdot q_1)(q_1\cdot q_2)$
$\frac(p-1)(q_1)\cdot \frac(p_2)(q_2)=\frac(p_1\cdot p_2)(q_1\cdot q_2)$

มีการแนะนำแผนกดังต่อไปนี้:
$\frac(p_1)(q_1):\frac(p_2)(q_2)=\frac(p_1)(q_1)\cdot \frac(q_2)(p_2)$

บนเซต $\mathbb(Q)$ สมการ $a\cdot x=b$ มีคำตอบเฉพาะสำหรับแต่ละ $a\neq 0$ (ไม่ได้กำหนดไว้ว่าการหารด้วยศูนย์) ซึ่งหมายความว่ามีองค์ประกอบผกผัน $\frac(1)(a)$ หรือ $a^(-1)$:
$(\forall a\in \mathbb(Q)\setminus\lbrace 0\rbrace)(\exists \frac(1)(a))(a\cdot \frac(1)(a)=\frac(1) (ก)\cdot a=a)$

ลำดับของเซต $\mathbb(Q)$ สามารถขยายได้ดังนี้:
$\frac(p_1)(q_1)

เซต $\mathbb(Q)$ มีหนึ่งอัน ทรัพย์สินที่สำคัญ: ระหว่างจำนวนตรรกยะสองตัวใดๆ จะมีจำนวนตรรกยะอื่นๆ มากมายเป็นอนันต์ ดังนั้นจึงไม่มีจำนวนตรรกยะสองตัวที่อยู่ติดกัน ต่างจากเซตของจำนวนธรรมชาติและจำนวนเต็ม

จำนวนอตรรกยะ $\mathbb(I)$

ตัวอย่างของจำนวนอตรรกยะ:
$0.333333...$
$\sqrt(2) \ประมาณ 1.41422135...$
$\pi\ประมาณ 3.1415926535...$

เนื่องจากระหว่างจำนวนตรรกยะสองตัวใดๆ ก็มีจำนวนตรรกยะอื่นๆ มากมายเป็นอนันต์ จึงเป็นเรื่องง่ายที่จะสรุปอย่างผิดพลาดว่าเซตของจำนวนตรรกยะมีความหนาแน่นมากจนไม่จำเป็นต้องขยายออกไปอีก แม้แต่พีทาโกรัสก็ยังทำผิดพลาดในสมัยของเขา อย่างไรก็ตาม ผู้ร่วมสมัยของเขาได้หักล้างข้อสรุปนี้แล้วเมื่อศึกษาคำตอบของสมการ $x\cdot x=2$ ($x^2=2$) บนเซตของจำนวนตรรกยะ ในการแก้สมการดังกล่าว จำเป็นต้องแนะนำแนวคิดเรื่องรากที่สอง จากนั้นคำตอบของสมการนี้จะอยู่ในรูปแบบ $x=\sqrt(2)$ สมการเช่น $x^2=a$ โดยที่ $a$ เป็นจำนวนตรรกยะที่ทราบ และ $x$ เป็นจำนวนที่ไม่ทราบ ไม่ได้มีคำตอบสำหรับเซตของจำนวนตรรกยะเสมอไป และอีกครั้งที่จำเป็นต้องขยายสมการ ชุด. ชุดของจำนวนอตรรกยะเกิดขึ้น และตัวเลขเช่น $\sqrt(2)$, $\sqrt(3)$, $\pi$... เป็นของชุดนี้

จำนวนจริง $\mathbb(R)$

การรวมกันของเซตของจำนวนตรรกยะและจำนวนอตรรกยะคือเซตของจำนวนจริง เนื่องจาก $\mathbb(Q)\subset \mathbb(R)$ จึงมีเหตุผลอีกครั้งที่จะถือว่าการดำเนินการทางคณิตศาสตร์และความสัมพันธ์ที่นำมาใช้ยังคงรักษาคุณสมบัติไว้ในชุดใหม่ การพิสูจน์อย่างเป็นทางการในเรื่องนี้เป็นเรื่องยากมาก ดังนั้นคุณสมบัติที่กล่าวมาข้างต้นของการดำเนินการทางคณิตศาสตร์และความสัมพันธ์ของเซตของจำนวนจริงจึงถูกนำมาใช้เป็นสัจพจน์ ในพีชคณิต วัตถุดังกล่าวเรียกว่าเขตข้อมูล ดังนั้นเซตของจำนวนจริงจึงเรียกว่าเขตข้อมูลเรียงลำดับ

เพื่อให้นิยามของเซตของจำนวนจริงสมบูรณ์ จำเป็นต้องแนะนำสัจพจน์เพิ่มเติมที่แยกเซต $\mathbb(Q)$ และ $\mathbb(R)$ สมมติว่า $S$ เป็นเซตย่อยที่ไม่ว่างของเซตจำนวนจริง องค์ประกอบ $b\in \mathbb(R)$ เรียกว่าขอบเขตบนของเซต $S$ ถ้า $\forall x\in S$ เก็บ $x\leq b$ จากนั้นเราบอกว่าชุด $S$ นั้นมีขอบเขตอยู่ด้านบน ขอบเขตบนที่เล็กที่สุดของชุด $S$ เรียกว่า supremum และเขียนแทนด้วย $\sup S$ แนวคิดของขอบเขตล่าง ชุดขอบเขตด้านล่าง และ infinum $\inf S$ ได้รับการแนะนำในทำนองเดียวกัน ตอนนี้สัจพจน์ที่หายไปมีการกำหนดดังนี้:

สับเซตที่ไม่ว่างและมีขอบเขตบนของเซตจำนวนจริงจะมีค่าสูงสุด
นอกจากนี้ยังสามารถพิสูจน์ได้ว่าฟิลด์ของจำนวนจริงที่กำหนดในลักษณะข้างต้นนั้นไม่ซ้ำกัน

จำนวนเชิงซ้อน$\mathbb(C)$

ตัวอย่างของจำนวนเชิงซ้อน:
$(1, 2), (4, 5), (-9, 7), (-3, -20), (5, 19),...$
$1 + 5i, 2 - 4i, -7 + 6i...$ โดยที่ $i = \sqrt(-1)$ หรือ $i^2 = -1$

เซตของจำนวนเชิงซ้อนแสดงถึงคู่ลำดับของจำนวนจริงทั้งหมด นั่นคือ $\mathbb(C)=\mathbb(R)^2=\mathbb(R)\times \mathbb(R)$ ซึ่งการดำเนินการของ การบวกและการคูณมีการกำหนดไว้ดังนี้:
$(a,b)+(c,d)=(a+b,c+d)$
$(a,b)\cdot (c,d)=(ac-bd,ad+bc)$

การเขียนจำนวนเชิงซ้อนมีอยู่หลายรูปแบบ ซึ่งรูปแบบที่พบบ่อยที่สุดคือ $z=a+ib$ โดยที่ $(a,b)$ คือคู่ของจำนวนจริง และตัวเลข $i=(0,1)$ เรียกว่าหน่วยจินตภาพ

มันง่ายที่จะแสดงว่า $i^2=-1$ การขยายเซต $\mathbb(R)$ ไปยังเซต $\mathbb(C)$ ช่วยให้เราสามารถหารากที่สองของ ตัวเลขติดลบซึ่งเป็นเหตุให้เกิดชุดจำนวนเชิงซ้อนขึ้นมา มันง่ายที่จะแสดงว่าเซตย่อยของเซต $\mathbb(C)$ กำหนดโดย $\mathbb(C)_0=\lbrace (a,0)|a\in \mathbb(R)\rbrace$, เป็นไปตามสัจพจน์ทั้งหมดสำหรับจำนวนจริง ดังนั้น $\mathbb(C)_0=\mathbb(R)$ หรือ $R\subset\mathbb(C)$

โครงสร้างพีชคณิตของเซต $\mathbb(C)$ ที่เกี่ยวข้องกับการดำเนินการบวกและการคูณมีคุณสมบัติดังต่อไปนี้:
1. การสับเปลี่ยนของการบวกและการคูณ
2. ความสัมพันธ์ของการบวกและการคูณ
3. $0+i0$ - องค์ประกอบที่เป็นกลางสำหรับการบวก
4. $1+i0$ - องค์ประกอบที่เป็นกลางสำหรับการคูณ
5. การคูณเป็นการแจกแจงด้วยการบวก
6. มีการผกผันเพียงตัวเดียวสำหรับทั้งการบวกและการคูณ

จำนวนตรรกยะ– จำนวนที่แสดงด้วยเศษส่วนธรรมดา m/n โดยที่ตัวเศษ m เป็นจำนวนเต็ม และตัวส่วน n เป็นจำนวนธรรมชาติ จำนวนตรรกยะใดๆ สามารถแสดงเป็นเศษส่วนทศนิยมอนันต์เป็นคาบได้ เซตของจำนวนตรรกยะเขียนแทนด้วย Q

หากจำนวนจริงไม่เป็นจำนวนตรรกยะ แสดงว่าเป็นเช่นนั้น จำนวนอตรรกยะ. เศษส่วนทศนิยมที่แสดงจำนวนอตรรกยะนั้นเป็นอนันต์และไม่เป็นคาบ เซตของจำนวนอตรรกยะมักจะแสดงด้วยตัวพิมพ์ใหญ่ I

เรียกว่าจำนวนจริง พีชคณิตถ้าเป็นรากของพหุนามบางตัว (ดีกรีที่ไม่ใช่ศูนย์) ที่มีค่าสัมประสิทธิ์ตรรกยะ จะมีการเรียกตัวเลขที่ไม่ใช่พีชคณิต เหนือธรรมชาติ.

คุณสมบัติบางอย่าง:

เซตของจำนวนตรรกยะตั้งอยู่ทุกจุดอย่างหนาแน่นบนเส้นจำนวน: ระหว่างจำนวนตรรกยะที่ต่างกันสองตัวใดๆ จะมีจำนวนตรรกยะอย่างน้อยหนึ่งตัว (และด้วยเหตุนี้ ชุดอนันต์สรุปตัวเลข). อย่างไรก็ตามปรากฎว่าชุดของจำนวนตรรกยะ Q และชุดของจำนวนธรรมชาติ N นั้นเท่ากันนั่นคือสามารถสร้างการติดต่อแบบหนึ่งต่อหนึ่งระหว่างพวกมันได้ (องค์ประกอบทั้งหมดของชุดของจำนวนตรรกยะสามารถกำหนดหมายเลขใหม่ได้) .

เซต Q ของจำนวนตรรกยะจะปิดภายใต้การบวก ลบ คูณ และหาร ซึ่งก็คือผลรวม ผลต่าง ผลคูณและผลหารของจำนวนตรรกยะสองตัว ก็เป็นจำนวนตรรกยะเช่นกัน

จำนวนตรรกยะทั้งหมดเป็นพีชคณิต (ตรงกันข้ามเป็นเท็จ)

จำนวนอดิศัยที่แท้จริงทุกจำนวนนั้นไม่มีเหตุผล

จำนวนอตรรกยะทุกจำนวนเป็นพีชคณิตหรือทิพย์

เซตของจำนวนอตรรกยะนั้นมีความหนาแน่นทุกจุดบนเส้นจำนวน: ระหว่างตัวเลขสองตัวใดๆ จะมีจำนวนอตรรกยะจำนวนหนึ่ง (และด้วยเหตุนี้จึงเป็นเซตของจำนวนอตรรกยะที่ไม่มีที่สิ้นสุด)

เซตของจำนวนอตรรกยะนับไม่ได้

เมื่อแก้ไขปัญหาจะสะดวกพร้อมกับจำนวนอตรรกยะ a + b√ c (โดยที่ a, b เป็นจำนวนตรรกยะ c เป็นจำนวนเต็มที่ไม่ใช่กำลังสองของจำนวนธรรมชาติ) เพื่อพิจารณาจำนวน "คอนจูเกต" a – b√ c: ผลบวกและผลคูณของจำนวนดั้งเดิม – จำนวนตรรกยะ ดังนั้น a + b√ c และ a – b√ c เป็นราก สมการกำลังสองด้วยสัมประสิทธิ์จำนวนเต็ม

ปัญหากับแนวทางแก้ไข

1. พิสูจน์ว่า

ก) หมายเลข √ 7;

b) บันทึกหมายเลข 80;

ค) หมายเลข √ 2 + 3 √ 3;

ไม่มีเหตุผล

ก) สมมติว่าตัวเลข √ 7 เป็นจำนวนตรรกยะ จากนั้นจะมีโคไพรม์ p และ q โดยที่ √ 7 = p/q ดังนั้นเราจะได้ p 2 = 7q 2 เนื่องจาก p และ q ค่อนข้างเป็นจำนวนเฉพาะ ดังนั้น p 2 ดังนั้น p จึงหารด้วย 7 ลงตัว จากนั้น p = 7k โดยที่ k เป็นจำนวนธรรมชาติ ดังนั้น q 2 = 7k 2 = pk ซึ่งขัดแย้งกับข้อเท็จจริงที่ว่า p และ q เป็นจำนวนเฉพาะ

ดังนั้นสมมติฐานจึงเป็นเท็จ ซึ่งหมายความว่าตัวเลข √ 7 นั้นไม่มีเหตุผล

b) ให้เราถือว่าบันทึกตัวเลข 80 เป็นจำนวนตรรกยะ จากนั้นจะมี p และ q โดยธรรมชาติซึ่ง log 80 = p/q หรือ 10 p = 80 q ซึ่งเราจะได้ 2 p–4q = 5 q–p เมื่อพิจารณาว่าตัวเลข 2 และ 5 ค่อนข้างเป็นจำนวนเฉพาะ เราพบว่าความเสมอภาคสุดท้ายเป็นไปได้สำหรับ p–4q = 0 และ q–p = 0 เท่านั้น โดยที่ p = q = 0 ซึ่งเป็นไปไม่ได้ เนื่องจาก p และ q ถูกเลือก ให้เป็นธรรมชาติ

ดังนั้นสมมติฐานจึงเป็นเท็จ ซึ่งหมายความว่าตัวเลข lg 80 นั้นไม่ลงตัว

c) ให้เราแสดงตัวเลขนี้ด้วย x

จากนั้น (x – √ 2) 3 = 3 หรือ x 3 + 6x – 3 = √ 2 (3x 2 + 2) หลังจากยกกำลังสองสมการนี้แล้ว เราพบว่า x ต้องเป็นไปตามสมการ

x 6 – 6x 4 – 6x 3 + 12x 2 – 36x + 1 = 0

ของเขา รากที่มีเหตุผลมีเพียงตัวเลข 1 และ –1 เท่านั้น การตรวจสอบแสดงว่า 1 และ –1 ไม่ใช่ราก

ดังนั้นตัวเลขที่กำหนด √ 2 + 3 √ 3 ​​​​จึงไม่มีเหตุผล

2. เป็นที่รู้กันว่าตัวเลข a, b, √ก –√ข,- มีเหตุผล. พิสูจน์ว่า √ก และ √ขยังเป็นจำนวนตรรกยะอีกด้วย

มาดูผลงานกัน

(√ ก – √ ข)·(√ ก + √ ข) = ก – ข

ตัวเลข √ก +√ข,ซึ่งเท่ากับอัตราส่วนของตัวเลข a – b และ √ก –√ข,เป็นจำนวนตรรกยะ เนื่องจากผลหารของจำนวนตรรกยะสองตัวคือจำนวนตรรกยะ ผลรวมของจำนวนตรรกยะสองตัว

½ (√ ก + √ ข) + ½ (√ ก – √ ข) = √ ก

– จำนวนตรรกยะ ผลต่าง

½ (√ ก + √ ข) – ½ (√ ก – √ ข) = √ ข

ก็เป็นจำนวนตรรกยะด้วยซึ่งเป็นสิ่งที่ต้องพิสูจน์

3. พิสูจน์ว่ามีจำนวนอตรรกยะบวก a และ b โดยที่จำนวน a b เป็นจำนวนธรรมชาติ

4. มีจำนวนตรรกยะ a, b, c, d ที่เป็นไปตามความเท่าเทียมกันหรือไม่

(ก + ข √ 2 ) 2n + (ค + d√ 2 ) 2n = 5 + 4√ 2 ,

โดยที่ n คือจำนวนธรรมชาติ?

หากความเท่าเทียมกันที่กำหนดในเงื่อนไขเป็นที่น่าพอใจ และตัวเลข a, b, c, d เป็นจำนวนตรรกยะ ความเท่าเทียมกันก็จะเป็นไปตามนั้นด้วย:

(ก–ข √ 2 ) 2n + (ค – d√ 2 ) 2n = 5 – 4√ 2.

แต่ 5 – 4√ 2 (a – b√ 2 ) 2n + (c – d√ 2 ) 2n > 0 ผลความขัดแย้งพิสูจน์ว่าความเสมอภาคเดิมนั้นเป็นไปไม่ได้

คำตอบ: พวกเขาไม่มีอยู่จริง

5. ถ้าส่วนที่มีความยาว a, b, c เป็นรูปสามเหลี่ยม ดังนั้น สำหรับ n ทั้งหมด = 2, 3, 4, . . . ส่วนที่มีความยาว n √ a, n √ b, n √ c ก็เป็นรูปสามเหลี่ยมเช่นกัน พิสูจน์สิ.

หากส่วนที่มีความยาว a, b, c ก่อตัวเป็นรูปสามเหลี่ยม แสดงว่าอสมการของสามเหลี่ยมจะให้มา

ดังนั้นเราจึงมี

(n √ a + n √ b) n > a + b > c = (n √ c) n

ยังไม่มีข้อความ √ ก + n √ ข > n √ ค

กรณีที่เหลือของการตรวจสอบอสมการของสามเหลี่ยมก็ถือว่าคล้ายกัน โดยมีข้อสรุปดังนี้

6. พิสูจน์ว่าเศษส่วนทศนิยมอนันต์ 0.1234567891011121314... (หลังจุดทศนิยม จำนวนธรรมชาติทั้งหมดจะเขียนตามลำดับ) เป็นจำนวนอตรรกยะ

ดังที่คุณทราบ จำนวนตรรกยะจะแสดงเป็นเศษส่วนทศนิยมซึ่งมีจุดเริ่มต้นจากเครื่องหมายที่กำหนด ดังนั้นจึงเพียงพอแล้วที่จะพิสูจน์ว่าเศษส่วนนี้ไม่มีคาบในสัญลักษณ์ใดๆ สมมติว่าไม่เป็นเช่นนั้น และลำดับ T ของตัวเลข n หลักคือคาบของเศษส่วน โดยเริ่มต้นที่จุดทศนิยมตำแหน่งที่ m เป็นที่ชัดเจนว่าในบรรดาตัวเลขหลังเครื่องหมาย m นั้นมีจำนวนที่ไม่เป็นศูนย์ดังนั้นจึงมีตัวเลขที่ไม่เป็นศูนย์ในลำดับของหลัก T ซึ่งหมายความว่า เริ่มจากหลักที่ m หลังจุดทศนิยม ในบรรดาตัวเลข n หลักใดๆ ในแถวจะมีตัวเลขที่ไม่ใช่ศูนย์ อย่างไรก็ตาม สัญกรณ์ทศนิยมของเศษส่วนนี้ต้องมีสัญกรณ์ทศนิยมของตัวเลข 100...0 = 10 k โดยที่ k > m และ k > n เห็นได้ชัดว่ารายการนี้เกิดขึ้นทางด้านขวาของหลักที่ m และมีศูนย์มากกว่า n ตัวติดกัน ดังนั้นเราจึงได้รับความขัดแย้งที่ทำให้การพิสูจน์สมบูรณ์

7. ให้เศษส่วนทศนิยมอนันต์ 0,a 1 a 2 ... . พิสูจน์ว่าตัวเลขในรูปแบบทศนิยมสามารถจัดเรียงใหม่ได้เพื่อให้เศษส่วนผลลัพธ์แสดงจำนวนตรรกยะ

จำไว้ว่าเศษส่วนจะแสดงจำนวนตรรกยะก็ต่อเมื่อมันเป็นคาบโดยเริ่มจากเครื่องหมายบางตัวเท่านั้น เราจะแบ่งตัวเลขตั้งแต่ 0 ถึง 9 ออกเป็นสองคลาส: ในคลาสแรกเราจะรวมตัวเลขที่ปรากฏในเศษส่วนดั้งเดิมเป็นจำนวนจำกัดในคลาสที่สองเรารวมตัวเลขที่ปรากฏในเศษส่วนดั้งเดิมด้วยจำนวนอนันต์ของ ครั้ง เรามาเริ่มเขียนเศษส่วนเป็นคาบซึ่งสามารถหาได้จากต้นฉบับโดยการจัดเรียงตัวเลขใหม่ ขั้นแรก หลังจากศูนย์และลูกน้ำ เราจะเขียนตัวเลขทั้งหมดจากคลาสแรกตามลำดับแบบสุ่ม โดยแต่ละครั้งจะมากเท่าที่ปรากฏในรูปแบบเศษส่วนดั้งเดิม ตัวเลขชั้นแรกที่บันทึกไว้จะนำหน้าจุดในส่วนที่เป็นเศษส่วนของทศนิยม ต่อไป เราจะเขียนตัวเลขจากชั้นเรียนที่สองทีละรายการตามลำดับ เราจะประกาศให้การรวมกันนี้เป็นช่วงเวลาและทำซ้ำเป็นจำนวนอนันต์ ดังนั้นเราจึงเขียนเศษส่วนคาบที่ต้องการเพื่อแสดงจำนวนตรรกยะที่แน่นอน

8. พิสูจน์ว่าในทุกเศษส่วนทศนิยมอนันต์มีลำดับของตำแหน่งทศนิยมที่มีความยาวตามใจชอบ ซึ่งเกิดขึ้นไม่สิ้นสุดหลายครั้งในการสลายตัวของเศษส่วน

ให้ m เป็นจำนวนธรรมชาติที่กำหนดมาโดยพลการ ลองแบ่งเศษส่วนทศนิยมอนันต์นี้ออกเป็นส่วนๆ โดยมีหลัก m ในแต่ละส่วน จะมีส่วนดังกล่าวจำนวนอนันต์ อีกด้านหนึ่ง ระบบต่างๆประกอบด้วยหลัก m มีเพียง 10 m คือจำนวนจำกัด ด้วยเหตุนี้ อย่างน้อยหนึ่งระบบเหล่านี้จึงต้องถูกทำซ้ำที่นี่หลายๆ ครั้งไม่จำกัด

ความคิดเห็น สำหรับจำนวนอตรรกยะ √ 2, π หรือ จเราไม่รู้ด้วยซ้ำว่าตัวเลขใดถูกทำซ้ำอย่างไม่สิ้นสุดหลายครั้งในเศษส่วนทศนิยมอนันต์ที่เป็นตัวแทน แม้ว่าแต่ละตัวเลขเหล่านี้สามารถพิสูจน์ได้อย่างง่ายดายว่ามีตัวเลขดังกล่าวที่แตกต่างกันอย่างน้อยสองหลัก

9. พิสูจน์เบื้องต้นว่า รากที่เป็นบวกสมการ

ไม่มีเหตุผล

สำหรับ x > 0 ทางด้านซ้ายของสมการจะเพิ่มขึ้นด้วย x และเห็นได้ง่ายว่าที่ x = 1.5 จะน้อยกว่า 10 และที่ x = 1.6 จะมากกว่า 10 ดังนั้น รากที่เป็นบวกเพียงตัวเดียวของ สมการอยู่ภายในช่วง (1.5 ; 1.6)

ขอให้เราเขียนรากเป็นเศษส่วนที่ลดไม่ได้ p/q โดยที่ p และ q เป็นจำนวนธรรมชาติที่ค่อนข้างเป็นจำนวนเฉพาะ จากนั้นที่ x = p/q สมการจะอยู่ในรูปแบบต่อไปนี้:

หน้า 5 + หน้า 4 = 10q 5

โดยที่ตามมาว่า p เป็นตัวหารของ 10 ดังนั้น p จึงเท่ากับหนึ่งในตัวเลข 1, 2, 5, 10 อย่างไรก็ตาม เมื่อเขียนเศษส่วนที่มีตัวเศษ 1, 2, 5, 10 เราจะสังเกตได้ทันทีว่า ไม่มีอันใดตกอยู่ในช่วง (1.5; 1.6)

ดังนั้น รากที่เป็นบวกของสมการดั้งเดิมจึงไม่สามารถแสดงเป็นเศษส่วนธรรมดาได้ ดังนั้นจึงเป็นจำนวนอตรรกยะ

10. ก) มีจุด A, B และ C สามจุดบนระนาบหรือไม่ ซึ่งสำหรับจุด X ใดๆ ความยาวของส่วน XA, XB และ XC อย่างน้อยหนึ่งจุดนั้นไม่มีเหตุผล

b) พิกัดของจุดยอดของรูปสามเหลี่ยมมีเหตุผล พิสูจน์ว่าพิกัดของจุดศูนย์กลางของเส้นรอบวงนั้นมีเหตุผลเช่นกัน

c) มีทรงกลมที่มีจุดตรรกยะจุดเดียวหรือไม่? (จุดตรรกยะคือจุดที่พิกัดคาร์ทีเซียนทั้งสามจุดเป็นจำนวนตรรกยะ)

ก) ใช่ มีอยู่จริง ให้ C เป็นจุดกึ่งกลางของส่วน AB จากนั้น XC 2 = (2XA 2 + 2XB 2 – AB 2)/2 หากตัวเลข AB 2 ไม่ลงตัว ตัวเลข XA, XB และ XC จะไม่สามารถเป็นจำนวนตรรกยะพร้อมกันได้

b) ให้ (a 1 ; b 1), (a 2 ; b 2) และ (a 3 ; b 3) เป็นพิกัดของจุดยอดของรูปสามเหลี่ยม พิกัดของจุดศูนย์กลางของวงกลมที่ล้อมรอบถูกกำหนดโดยระบบสมการ:

(x – ก 1) 2 + (y – ข 1) 2 = (x – ก 2) 2 + (y – ข 2) 2,

(x – ก 1) 2 + (y – ข 1) 2 = (x – ก 3) 2 + (y – ข 3) 2.

ง่ายต่อการตรวจสอบว่าสมการเหล่านี้เป็นเส้นตรง ซึ่งหมายความว่าการแก้ระบบสมการที่พิจารณานั้นเป็นเหตุผล

c) มีทรงกลมดังกล่าวอยู่ เช่น ทรงกลมที่มีสมการ

(x – √ 2 ) 2 + y 2 + z 2 = 2

จุด O ที่มีพิกัด (0; 0; 0) เป็นจุดเหตุผลที่วางอยู่บนทรงกลมนี้ จุดที่เหลือของทรงกลมนั้นไม่มีเหตุผล มาพิสูจน์กัน

ให้เราสมมติสิ่งที่ตรงกันข้าม: ให้ (x; y; z) เป็นจุดตรรกยะของทรงกลม แตกต่างจากจุด O เห็นได้ชัดว่า x แตกต่างจาก 0 เนื่องจากที่ x = 0 มีวิธีแก้ปัญหาเฉพาะ (0; 0; 0) ซึ่งขณะนี้เราไม่สามารถสนใจได้ เปิดวงเล็บแล้วแสดง √ 2:

x 2 – 2√ 2 x + 2 + y 2 + z 2 = 2

√ 2 = (x 2 + y 2 + z 2)/(2x)

ซึ่งไม่สามารถเกิดขึ้นได้กับตรรกยะ x, y, z และอตรรกยะ √ 2 ดังนั้น O(0; 0; 0) จึงเป็นจุดเหตุผลเพียงจุดเดียวบนทรงกลมที่อยู่ระหว่างการพิจารณา

ปัญหาที่ไม่มีวิธีแก้ไข

1. พิสูจน์ว่าจำนวนนั้น

\[ \sqrt(10+\sqrt(24)+\sqrt(40)+\sqrt(60)) \]

ไม่มีเหตุผล

2. ความเท่าเทียมกัน (5 + 3√ 2 ) m = (3 + 5√ 2 ) n มีค่าเท่ากับจำนวนเท่าใด m และ n?

3. มีตัวเลขใดที่ตัวเลข a – √ 3 และ 1/a + √ 3 เป็นจำนวนเต็มหรือไม่?

4. ตัวเลข 1, √ 2, 4 สามารถเป็นสมาชิก (ไม่จำเป็นต้องอยู่ติดกัน) ของการก้าวหน้าทางคณิตศาสตร์ได้หรือไม่?

5. พิสูจน์ว่าสำหรับจำนวนธรรมชาติใดๆ n สมการ (x + y√ 3) 2n = 1 + √ 3 ไม่มีคำตอบเป็นจำนวนตรรกยะ (x; y)

นักคณิตศาสตร์โบราณรู้อยู่แล้วเกี่ยวกับส่วนของความยาวหนึ่งหน่วย ตัวอย่างเช่น พวกเขารู้ความไม่ลงตัวของเส้นทแยงมุมและด้านข้างของสี่เหลี่ยมจัตุรัส ซึ่งเทียบเท่ากับความไม่ลงตัวของตัวเลข

ไม่มีเหตุผลคือ:

ตัวอย่างการพิสูจน์ความไร้เหตุผล

รากของ 2

ให้เราสมมติสิ่งที่ตรงกันข้าม: มันเป็นตรรกยะ กล่าวคือ มันถูกแสดงในรูปของเศษส่วนที่ลดไม่ได้ โดยที่ และ เป็นจำนวนเต็ม ลองยกกำลังสองของความเท่าเทียมกัน:

.

ตามมาด้วยว่าคู่เป็นคู่ และ ปล่อยให้มันเป็นที่ทั้งหมด แล้ว

ดังนั้นแม้แต่ หมายถึงคู่ และ เราพบสิ่งนั้น และ เป็นจำนวนคู่ ซึ่งขัดแย้งกับการลดทอนไม่ได้ของเศษส่วน . ซึ่งหมายความว่าสมมติฐานเดิมไม่ถูกต้อง และเป็นจำนวนอตรรกยะ

ลอการิทึมไบนารีของจำนวน 3

ให้เราสมมติสิ่งที่ตรงกันข้าม: มันเป็นตรรกยะ นั่นคือ มันถูกแสดงเป็นเศษส่วน โดยที่ และ เป็นจำนวนเต็ม เนื่องจาก และ สามารถเลือกให้เป็นค่าบวกได้ แล้ว

แต่แม้และแปลก เราได้รับความขัดแย้ง

จ

เรื่องราว

แนวคิดเรื่องจำนวนอตรรกยะถูกนำมาใช้โดยปริยายโดยนักคณิตศาสตร์ชาวอินเดียในศตวรรษที่ 7 ก่อนคริสต์ศักราช เมื่อ Manava (ประมาณ 750 ปีก่อนคริสตกาล - ประมาณ 690 ปีก่อนคริสตกาล) พบว่า รากที่สองจำนวนธรรมชาติบางตัว เช่น 2 และ 61 ไม่สามารถแสดงอย่างชัดเจนได้

การพิสูจน์ครั้งแรกของการมีอยู่ของจำนวนอตรรกยะมักมาจากฮิปปาซัสแห่งเมตาปอนตัส (ประมาณ 500 ปีก่อนคริสตกาล) ซึ่งเป็นชาวพีทาโกรัสที่พบข้อพิสูจน์นี้โดยการศึกษาความยาวของด้านข้างของรูปดาวห้าแฉก ในสมัยพีทาโกรัส เชื่อกันว่ามีหน่วยความยาวหน่วยเดียว ซึ่งมีขนาดเล็กเพียงพอและแบ่งแยกไม่ได้ ซึ่งเข้าสู่ส่วนใดๆ ก็ตามด้วยจำนวนเต็มครั้ง อย่างไรก็ตาม ฮิปปาซัสแย้งว่าไม่มีหน่วยความยาวเดียว เนื่องจากการสันนิษฐานว่ามีอยู่จริงทำให้เกิดความขัดแย้ง เขาแสดงให้เห็นว่าถ้าด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉากหน้าจั่วมีจำนวนส่วนของหน่วยเป็นจำนวนเต็ม จำนวนนี้จะต้องเป็นทั้งเลขคู่และคี่ หลักฐานมีลักษณะดังนี้:

• อัตราส่วนของความยาวของด้านตรงข้ามมุมฉากต่อความยาวของขาของสามเหลี่ยมมุมฉากหน้าจั่วสามารถแสดงได้เป็น ก:ข, ที่ไหน กและ ขเลือกให้เล็กที่สุดเท่าที่จะเป็นไปได้
• ตามทฤษฎีบทพีทาโกรัส: ก² = 2 ข².
• เพราะ ก- สม่ำเสมอ, กต้องเป็นเลขคู่ (เนื่องจากกำลังสองของเลขคี่จะเป็นเลขคี่)
• เพราะว่า ก:ขลดไม่ได้ ขจะต้องแปลก
• เพราะ กแม้เราจะแสดงถึง ก = 2ย.
• แล้ว ก² = 4 ย² = 2 ข².
• ข² = 2 ย² ดังนั้น ข- ถึงอย่างนั้น ขสม่ำเสมอ.
• อย่างไรก็ตามได้รับการพิสูจน์แล้วว่า ขแปลก. ความขัดแย้ง.

นักคณิตศาสตร์ชาวกรีกเรียกอัตราส่วนนี้ของปริมาณที่เทียบไม่ได้ อะโลโกส(พูดไม่ได้) แต่ตามตำนานพวกเขาไม่ได้ให้ความเคารพต่อฮิปปาซัส มีตำนานเล่าว่าฮิปปาซัสค้นพบระหว่างการเดินทางในทะเลและถูกชาวพีทาโกรัสคนอื่นๆ โยนลงน้ำ "สำหรับการสร้างองค์ประกอบของจักรวาลที่ปฏิเสธหลักคำสอนที่ว่าเอนทิตีทั้งหมดในจักรวาลสามารถลดจำนวนลงเป็นจำนวนเต็มและอัตราส่วนได้" การค้นพบฮิปปาซัสก่อให้เกิดปัญหาร้ายแรงสำหรับคณิตศาสตร์พีทาโกรัส โดยทำลายสมมติฐานที่ว่าตัวเลขและวัตถุทางเรขาคณิตเป็นหนึ่งเดียวกันและแยกจากกันไม่ได้

ดูสิ่งนี้ด้วย

หมายเหตุ

ระบบตัวเลข
การนับ ชุด	จำนวนธรรมชาติ () จำนวนเต็ม ()

บทที่แรก

แนวคิดเรื่องจำนวนอตรรกยะ

183. ปริมาณสมส่วนและไม่สมส่วนกับหน่วย

ดังที่ทราบจากเรขาคณิต การวัดทั่วไปของส่วนของเส้นตรงสองส่วนหรือสองมุมหรือสองส่วนโค้งที่มีรัศมีเดียวกัน โดยทั่วไปแล้วค่าสองค่าของปริมาณเท่ากันและสามค่าคือค่าของปริมาณนี้ที่มีอยู่ ในแต่ละอันมีจำนวนเต็มครั้งโดยไม่มีเศษเหลือ ในเรขาคณิต มีการอธิบายว่าอาจมีสองส่วนที่ไม่มีการวัดร่วมกัน (เช่น ด้านของสี่เหลี่ยมจัตุรัสและเส้นทแยงมุม)

ค่าสองค่าที่มีปริมาณเท่ากันเรียกว่าสมส่วนหรือไม่สามารถเทียบเคียงกันได้ขึ้นอยู่กับว่ามีการวัดร่วมกันหรือไม่

184. แนวคิดของการวัดสมมติว่าคุณต้องการวัดความยาวของส่วน เอบี โดยใช้หน่วยความยาว ซีดี .

เมื่อต้องการทำเช่นนี้ เราจะหาได้ว่าหน่วยหนึ่งมีกี่ครั้ง ซีดี บรรจุใน เอบี . ปล่อยให้ปรากฎว่ามีอยู่ในนั้น เอบี 3 ครั้ง เหลืออีกนิดหน่อย อีวี เล็กลง ซีดี . จากนั้นเลข 3 จะเป็นผลการวัดโดยประมาณที่มีความแม่นยำ 1 และยิ่งไปกว่านั้นยังมีข้อเสียเนื่องจาก เอบี มากกว่า 3ซีดี แต่น้อยกว่า 4ซีดี (เลข 4 ยังสามารถเรียกได้ว่าเป็นผลลัพธ์การวัดโดยประมาณที่มีความแม่นยำ 1 แต่มีส่วนเกิน)

หากต้องการผลการวัดที่แม่นยำยิ่งขึ้น เราจะหาจำนวนที่เหลือ อีวี ประกอบด้วยเศษส่วนบางส่วนของหน่วย ซีดี , เช่น. 1/10 ซีดี . ให้เราถือว่าเศษส่วนนี้มีอยู่ใน อีวี มากกว่า 8 แต่น้อยกว่า 9 ครั้ง จากนั้นตัวเลข 3.8 และ 3.9 จะเป็นผลลัพธ์โดยประมาณของการวัดส่วน เอบี แม่นถึง 1/10 ตัวแรกขาด ตัวที่สองเกิน

หากต้องการได้ผลลัพธ์การวัดที่แม่นยำยิ่งขึ้น เราจะหาจำนวนครั้งที่ 1/100 อยู่ในส่วนที่เหลือสุดท้าย ส่วนแบ่งหน่วย ซีดี . สมมติว่าเศษส่วนนี้มีอยู่ในเศษมากกว่า 5 ครั้ง แต่น้อยกว่า 6 ครั้ง จากนั้นตัวเลข 3.85 และ 3.86 จะเป็นผลลัพธ์โดยประมาณของการวัดส่วน เอบี แม่นยำถึง 1/100 ของหน่วย คุณสามารถวัดต่อไปเรื่อยๆ จนกว่าจะไม่มีเศษเหลือ หรือเศษเหลือน้อยจนสามารถละเลยได้ ในกรณีแรกเราจะได้รับผลการวัดที่แน่นอน ในกรณีที่สอง ซึ่งเป็นค่าโดยประมาณที่มีความแม่นยำเท่ากับเศษส่วนของหน่วยที่เราวัดครั้งล่าสุด

ถ้าเป็นเซ็กเมนต์ เอบี ไม่สมส่วนกับหน่วยความยาว ซีดี เราก็จะไม่มีทางได้ผลลัพธ์การวัดที่แม่นยำเลย จริงๆ แล้ว ถ้าเราสมมุติว่าผลลัพธ์ดังกล่าวจะเป็นเศษส่วนจำนวนหนึ่ง เป็นต้น 59/27 จากนั้น 1/27 แชร์ ซีดี จะทำหน้าที่เป็นมาตรการทั่วไปสำหรับ เอบี และ ซีดี และส่วนที่ไม่สามารถเทียบเคียงได้ก็ไม่มีมาตรการร่วมกัน

ถ้าเป็นเซ็กเมนต์ เอบีสมกับ ซีดี แล้วเราจะได้ผลลัพธ์การวัดที่แม่นยำหากเราพบการวัดทั่วไปในครั้งแรก เอบี และ ซีดี และพบว่าบรรจุอยู่กี่ครั้ง เอบี และ ซีดี . ถ้าให้เราถือว่าการวัดทั่วไปใน เอบี มีอยู่ 23 ครั้ง และใน ซีดี 11 ครั้งแล้ว เอบี = 23 / 11 ยูนิต ซีดี . แต่หากเราไม่ได้มองหาการวัดทั่วไป เราทำการวัดโดยใช้เศษส่วนของหน่วยที่สุ่มเลือกมาเอง ในกรณีนี้ เรามักจะไม่ได้ผลลัพธ์การวัดที่แม่นยำ

การวัดส่วนใหญ่มักทำในรูปแบบทศนิยมของหน่วย จากนั้นผลการวัดจะแสดงเป็นเศษส่วนทศนิยม เมื่อส่วนที่วัดได้สมส่วนกับหน่วยความยาว เศษส่วนทศนิยมอาจเป็นแบบจำกัด (หากการวัดทั่วไปเป็นเศษส่วนทศนิยมของหน่วย) หรือไม่มีที่สิ้นสุด (เมื่อการวัดทั่วไปเป็นเศษส่วนของหน่วยที่ไม่ ให้กลายเป็นเศษส่วนทศนิยมพอดี) หากส่วนที่วัดไม่สมส่วนกับหน่วยความยาว จะไม่สามารถให้ผลลัพธ์ที่แน่นอนของการวัดได้ ดังนั้นเศษส่วนทศนิยมจะต้องกลายเป็นอนันต์ (หากการวัดดำเนินต่อไปเรื่อยๆ โดยไม่มีที่สิ้นสุด)

ควรสังเกตว่ามีความแตกต่างอย่างมีนัยสำคัญระหว่างเศษส่วนทศนิยมอนันต์ที่สามารถได้รับจากการวัดส่วนที่สมส่วนกับส่วนที่มาจากการวัดส่วนที่ไม่สามารถเทียบเคียงได้ เศษส่วนแรกต้องเป็นแบบคาบ ส่วนที่สองไม่ใช่แบบคาบ

185. จำนวนอตรรกยะจำนวนเต็ม เศษส่วน ทศนิยมจำกัด และทศนิยมเป็นคาบ เรียกรวมกันว่าจำนวนตรรกยะ เศษส่วนทศนิยมที่ไม่ใช่คาบเรียกว่า ไม่มีเหตุผลตัวเลข แบบแรกทำหน้าที่เป็นหน่วยวัดปริมาณที่สมส่วนกับหนึ่ง ส่วนแบบหลังใช้เป็นหน่วยวัดปริมาณที่ไม่สามารถเทียบเคียงกับหนึ่งได้

จำนวนอตรรกยะจะถือว่าทราบ (หรือกำหนด) หากมีการระบุวิธีการซึ่งสามารถหาทศนิยมจำนวนเท่าใดก็ได้

จำนวนอตรรกยะสองตัว (เช่น จำนวนตรรกยะสองตัว) จะถือว่าเท่ากันหากมาจากการวัดปริมาณที่เท่ากันสองจำนวนด้วยหน่วยเดียวกัน จากจำนวนที่ไม่เท่ากันสองตัว จำนวนที่มากกว่านั้นถือเป็นจำนวนที่มาจากการวัดปริมาณที่มากขึ้น สอง ค่าที่เท่ากันแน่นอนว่าจะต้องมีจำนวนหน่วยทั้งหมดเท่ากัน จำนวนในสิบเท่ากัน จำนวนในร้อยเท่ากัน เป็นต้น ดังนั้น จำนวนอตรรกยะที่เท่ากันจึงต้องแสดงด้วยจำนวนเดียวกัน ค่าที่มากกว่าจะต้องมีจำนวนเต็มจำนวนมากกว่า หรือ - หากจำนวนเต็มเท่ากัน จำนวนในสิบที่มากกว่า หรือ - หากจำนวนเต็มและสิบเท่ากัน - จำนวนที่มากกว่าคือหนึ่งในร้อย เป็นต้น ตัวอย่างเช่น หมายเลข 2.745037 .. มากกว่าตัวเลข 2 ,745029... เนื่องจากในหลักที่ 6 แรกจะแสดงตัวเลขที่มากกว่าหลักที่ 6 ในวินาที ถ้าตัวเลขก่อนหน้าทั้งหมดเหมือนกัน

ตัวเลขที่ไม่ลงตัวอาจเป็นค่าบวกหรือลบก็ได้ ขึ้นอยู่กับว่าตัวเลขนั้นวัดปริมาณที่ถือว่าเป็นค่าบวกหรือปริมาณที่ถือว่าเป็นค่าลบ

186. ค่าประมาณของจำนวนอตรรกยะให้เราได้รับจำนวนอตรรกยะบ้าง α นั่นคือ ให้ระบุวิธีการที่เราสามารถรับตัวเลขได้มากเท่าที่เราต้องการ α (เช่น วิธีการนี้อาจเป็นกฎที่ใช้หาค่ารากที่สองโดยประมาณซึ่งมีความแม่นยำ 1/10 ถึง 1/100 ถึง 1/1000 เป็นต้น) สมมติว่าเราพบตัวเลข 5 หลักต่อไปนี้ α :

α = 1,4142...

ลองเอาตัวเลขสองสามตัวแรก เช่น ตัวเลข 1.41 แล้วทิ้งที่เหลือไป จากนั้นเราจะได้ค่าประมาณของตัวเลข α และค่านี้จะมีข้อเสียเนื่องจาก 1.41< α . หากเราเพิ่มตัวเลขสุดท้ายที่เราเก็บไว้ 1 เช่น แทนที่จะเป็น 1.41 เรารับ 1.42 เราก็จะได้ค่าโดยประมาณของตัวเลขด้วย α แต่เกินเลยไป. โดยปกติ จากค่าประมาณสองค่า โดยค่าหนึ่งขาดและอีกค่าเกิน ค่าที่ขาดจะถูกใช้หากหลักแรกที่ทิ้งน้อยกว่า 5 และค่าที่เกินหากหลักนี้มากกว่า 5

187. คำจำกัดความของการกระทำกับจำนวนอตรรกยะอนุญาต α และ β จะมีบางค่าที่ให้มาเป็นจำนวนอตรรกยะบวก หากระบุตัวเลขเหล่านี้แสดงว่าเราสามารถค้นหาค่าโดยประมาณได้อย่างแม่นยำ สมมุติว่าค่าโดยประมาณของตัวเลข α และ β โดยมีข้อเสียเปรียบจะเป็นดังนี้ (เราใช้ค่าประมาณ √3 และ √2):

(การประมาณที่สอดคล้องกันจะได้ส่วนที่เกินจากตัวเลขเหล่านี้โดยการเพิ่มทศนิยมตำแหน่งสุดท้ายขึ้น 1)

แล้ว: ก)พับ α และ β หมายถึงการหาตัวเลขที่จะเป็น

เช่น. การเพิ่มตัวเลข α และ β หมายถึงการค้นหาตัวเลขที่สามที่จะมากกว่าผลรวมของค่าประมาณใด ๆ ที่ถ่ายโดยมีข้อบกพร่อง แต่น้อยกว่าผลรวมของค่าประมาณใด ๆ ที่ถ่ายด้วยส่วนที่เกิน

ข)การหาตัวเลขโดยประมาณ α และ β ที่ระบุตอนนี้เราสามารถพูดได้ว่าผลิตภัณฑ์ α β มีตัวเลขอยู่จำนวนหนึ่ง

นั่นคือการคูณตัวเลข α และ β หมายถึงการค้นหาตัวเลขตัวที่สามที่จะมากกว่าผลคูณของค่าประมาณใดๆ ของมัน โดยถือว่ามีข้อบกพร่อง แต่น้อยกว่าผลคูณของค่าโดยประมาณใดๆ ของมัน โดยนำมาด้วย ส่วนเกิน.

วี) ในการเพิ่มจำนวนอตรรกยะ α ให้เป็นกำลังที่สอง สาม สี่ ฯลฯ หมายถึงการค้นหาผลคูณที่ประกอบด้วยตัวประกอบ 2, 3, 4 ฯลฯ ที่เท่ากับ α

d) การกระทำผกผันถูกกำหนดไว้สำหรับจำนวนอตรรกยะในลักษณะเดียวกับการกระทำที่มีเหตุผล ดังนั้นให้ลบออกจากตัวเลข α ตัวเลข β หมายถึงการหาตัวเลขดังกล่าว เอ็กซ์ เพื่อให้เป็นจำนวนเงิน β + เอ็กซ์ เท่าเทียมกัน α และอื่นๆ

ถ้าเป็นตัวเลขตัวใดตัวหนึ่ง α หรือ β จะเป็นเหตุผลจากนั้นในคำจำกัดความที่ระบุของการกระทำโดยตรงแทนที่จะใช้ค่าโดยประมาณของตัวเลขดังกล่าวเราสามารถใช้จำนวนที่แน่นอนได้

ผลคูณของจำนวนอตรรกยะและศูนย์จะถือว่าเท่ากับศูนย์สำหรับจำนวนตรรกยะ

การดำเนินการกับจำนวนอตรรกยะลบจะดำเนินการตามกฎที่กำหนดสำหรับจำนวนลบตรรกยะ

เมื่อตรวจสอบอย่างใกล้ชิดก็สรุปได้ว่า การกระทำกับจำนวนตรรกยะมีคุณสมบัติเหมือนกับการกระทำกับจำนวนตรรกยะ ; ตัวอย่างเช่น ผลรวมและผลิตภัณฑ์มีคุณสมบัติการสับเปลี่ยนและการเชื่อมโยง ผลิตภัณฑ์และการแบ่งส่วนยังมีคุณสมบัติการกระจายตัวอีกด้วย คุณสมบัติที่แสดงโดยอสมการจะถูกสงวนไว้สำหรับจำนวนอตรรกยะ แล้วถ้า α > β , ที่ α + γ > β, αγ > βγ (ถ้า γ > 0) และ αγ < βγ (ถ้า γ < 0) เป็นต้น

บทที่สอง

ความหมายที่ไม่ลงตัวของอนุมูล

188. รากโดยประมาณของระดับใดก็ได้เราได้กล่าวไปแล้ว (แผนก 7 บทที่ 2 §§ 175-177) รากที่สองโดยประมาณมีความแม่นยำสูงสุด 1, สูงสุด 1/10 เป็นต้น และรากเหล่านี้ตั้งอยู่อย่างไร สิ่งที่พูดไปแล้วเกี่ยวกับรากที่สองสามารถนำไปใช้กับรากของกำลังอื่นๆ ได้ เช่น ประมาณ 3 √2 ที่มีความแม่นยำ 1/100 เป็นเศษส่วนทศนิยมที่ประกอบด้วยจำนวนเต็ม ส่วนที่สิบ และส่วนร้อย ซึ่งกำลังสามมีค่าน้อยกว่า 2 แต่ถ้าเราเพิ่มขึ้น 1/100 แล้วเพิ่มเศษส่วนที่เพิ่มขึ้นนี้ให้เป็น ลูกบาศก์ เราได้เพิ่มอีก 2

เราจะไม่ใช้กฎเกณฑ์ในการค้นหารากของลูกบาศก์และกำลังที่สูงกว่าอื่นๆ ที่แน่นอนและโดยประมาณ ให้เราจำกัดตัวเองเพียงระบุวิธีการง่ายๆ ต่อไปนี้ในการค้นหารากดังกล่าว ให้คุณต้องหา 3 √2. รากโดยประมาณที่มีความแม่นยำ 1 จะเป็นตัวเลข 1 (มีข้อบกพร่อง) และ 2 (มีส่วนเกิน) อย่างชัดเจน หากต้องการค้นหาจำนวนหนึ่งในสิบของรากที่ต้องการ เราจะพบในชุด:

1; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2

ตัวเลขที่อยู่ติดกันสองตัวโดยที่ลูกบาศก์ของตัวเลขด้านซ้ายน้อยกว่า 2 และลูกบาศก์ของตัวเลขด้านขวามากกว่า 2 เมื่อต้องการทำสิ่งนี้ ให้นำค่าเฉลี่ย 1.5 จากตัวเลขในชุดข้อมูลของเราแล้วยกให้เป็นลูกบาศก์ เราจะพบว่า: 1.5 3 = 3.375 ซึ่งมากกว่า 2 เนื่องจากตัวเลขทางขวาของ 1.5 ให้มากกว่าเมื่อยกเป็นลูกบาศก์ เราจึงสามารถทิ้งครึ่งขวาทั้งหมดของอนุกรมและทดสอบเฉพาะตัวเลขเท่านั้น:

1; 1,1; 1,2; 1,3; 1,4.

ลองหาค่าเฉลี่ยของพวกเขา 1.2 แล้วยกให้เป็นลูกบาศก์ เราได้ 1.728 ซึ่งน้อยกว่า 2 ซึ่งหมายความว่าขณะนี้มีเพียงตัวเลข 1.3 และ 1.4 เท่านั้นที่ต้องถูกทดสอบ เมื่อยกเลข 1.3 ขึ้นมาเป็นลูกบาศก์ เราจะได้ 2.197 ซึ่งมากกว่า 2 เราจึงได้ตัวเลข 1.2 และ 1.3 สองตัวซึ่งต่างกัน 0.1 และระหว่างลูกบาศก์ที่มีเลข 2 อยู่ สิ่งเหล่านี้จะเป็น รากลูกบาศก์โดยประมาณของ 2 โดยมีความแม่นยำ 1/10 โดยมีข้อบกพร่องและส่วนเกิน หากเราต้องการหาหลักร้อยเราต้องลองใช้ตัวเลขต่อไปนี้:

1,21; 1,22; 1,23;.......1,29.

เมื่อนำค่าเฉลี่ย 1.25 ในชุดนี้มาบวกเป็นลูกบาศก์ เราจะพบว่า 1.25 3 = 1.953125 ซึ่งน้อยกว่า 2 ซึ่งหมายความว่าตอนนี้เราเพียงต้องทดสอบตัวเลข: 1.26; 1.27; 1.28; 1.29. เนื่องจาก 1.25 3 แตกต่างจาก 2 เพียงเล็กน้อย จึงมีโอกาสมากที่ 1.26 3 จะมากกว่า 2 และแน่นอนว่า เมื่อเพิ่ม 1.26 เข้าไปในลูกบาศก์ เราจะได้ 2.000376 ซึ่งหมายความว่ารากที่สามที่ต้องการของ 2 ซึ่งมีความแม่นยำ 1/100 จะเป็น 1.25 (มีข้อบกพร่อง) หรือ 1.26 (มีส่วนเกิน) หากเราต้องการหาจำนวนหนึ่งในพันเพิ่มเติม เราจะต้องทดสอบจำนวนอนุกรมด้วยวิธีที่คล้ายกัน:

1,251; 1,252; 1,253;.........1,259.

แน่นอนว่าเทคนิคนี้น่าเบื่อ (มีวิธีที่สะดวกกว่า) แต่ก็แสดงให้เห็นชัดเจนว่าเลขฐานสิบของรากโดยประมาณของกำลังใด ๆ สามารถพบได้ในจำนวนมาก

189. ความหมายที่ไม่ลงตัวของรากให้เราชี้แจงว่า √3 ซึ่งไม่ได้แสดงเป็นจำนวนเต็มหรืออย่างแน่นอน จำนวนเศษส่วนเท่ากับจำนวนอตรรกยะจำนวนหนึ่ง ในการทำเช่นนี้ เราคำนวณชุดค่าประมาณ √3 ด้วยความแม่นยำ 1/10 สูงถึง 1/100 สูงถึง 1/1000...

ค่าเหล่านี้จะเป็น:

1.7; 1.73; 1.732; 1.7320 (จากสัปดาห์) 1.8; 1.74; 1.733; 1.7321 (ไม่รวม)

ลองพลอตตัวเลขทั้งหมดนี้บนเส้นจำนวนกัน ในการทำเช่นนี้เราใช้จุด A บนเส้นบางเส้นเป็นจุดเริ่มต้นของส่วนต่างๆ และเลือกหน่วยความยาวใดก็ได้ พล็อตส่วนต่างๆ บนเส้นตรง: เเอบ 1 = 1,7 , เเอบ 2 = 1.73 เป็นต้น; จากนั้นส่วนต่างๆ: เเอบ 1 = 1,8, เเอบ 2 =1.74 เป็นต้น

เนื่องจากแต่ละรากโดยประมาณที่มีข้อบกพร่องน้อยกว่าแต่ละรากโดยประมาณที่มีส่วนเกิน (เนื่องจากกำลังสองของรากแรกน้อยกว่า 3 และกำลังสองของรากที่สองมากกว่า 3) ดังนั้นลูกสาวแต่ละคน ข ต้องนอนด้านซ้ายของแต่ละจุด ใน . ในทางกลับกัน ความแตกต่างระหว่างรากโดยประมาณที่มีส่วนเกินกับรากโดยประมาณที่สอดคล้องกันซึ่งมีข้อบกพร่องสามารถทำให้มีขนาดเล็กลงได้ตามต้องการ ดังนั้น ด้วยความแม่นยำที่เพิ่มขึ้นอย่างไม่จำกัด ซึ่งเราจะพบรากที่สองโดยประมาณของ 3 ซึ่งเป็นช่วงเวลาบนเส้นจำนวนที่แยกขอบเขตของจุด B ออกจากขอบเขตของจุด B (เช่น ช่วงเวลา ข 1 บี 1 , ข 2 บี 2 , ข 3 บี 3 ..) จะเล็กลงเรื่อยๆ และเล็กลงได้ตามต้องการ ภายใต้เงื่อนไขเหล่านี้ เราต้องถือว่ามีจุดใดจุดหนึ่งบนเส้น เอ็กซ์ (และมีเพียงอันเดียว) ซึ่งทำหน้าที่เป็นเขตแดนที่แยกส่วนของเส้นตรงที่จุดทั้งหมดอยู่ ข จากส่วนนั้นซึ่งมีจุดทั้งหมดอยู่ ใน .

เรามาแสดงด้วยตัวอักษรกัน α ตัวเลขที่วัดส่วน โอ้ . เนื่องจากตัวเลขนี้มากกว่าตัวเลขแต่ละตัวที่วัดส่วนต่างๆ เเอบ 1 ,เเอบ 2 ... และน้อยกว่าตัวเลขแต่ละตัวที่วัดส่วนต่างๆ เอบี 1 , เอบี 2 . . ., ที่ α 2 ต้องมากกว่ากำลังสองของแต่ละรากที่สองโดยประมาณของ 3 ที่นำมาด้วยส่วนที่ขาด และน้อยกว่ากำลังสองของแต่ละรากที่สองโดยประมาณของ 3 ที่นำมาด้วยส่วนที่เกิน ตามคำนิยามของรากที่สองโดยประมาณ จำนวนดังกล่าวคือ 3 ดังนั้น α 2 = 3 และดังนั้น α = √3

ทำซ้ำทุกอย่างที่พูด o √3 เกี่ยวกับรากของระดับใด ๆ ของจำนวนใด ๆ (แน่นอนว่าเป็นบวกเนื่องจากเรากำลังพูดถึง รากเลขคณิต) เราก็บอกได้ว่าจะเป็นเลขอะไรก็ตาม เอ, เสมอ m√ก มีจำนวนจำนวนหนึ่ง เป็นตรรกยะหรืออตรรกยะ ม กำลัง th เท่ากับก.

ดังนั้น คุณสมบัติทั้งหมดของอนุมูลตามคำจำกัดความของรากนี้ (มาตรา 6 บทที่ 6 § 168) ก็ใช้กับความหมายที่ไม่ลงตัวได้เช่นกัน ดังนั้น ไม่ว่าจำนวนบวกจะเป็นเท่าใด เราจะได้เสมอ:

บทที่สาม

แนวคิดของการคำนวณโดยประมาณ

190. บันทึกเบื้องต้น.เมื่อดำเนินการใด ๆ กับจำนวนอตรรกยะ (หรือจำนวนตรรกยะหากแสดงเป็นเศษส่วนทศนิยมที่มีจำนวนหลักมาก) เราจะต้องพอใจกับผลลัพธ์โดยประมาณของการกระทำ ในกรณีนี้ สิ่งสำคัญคือต้องทราบว่าผลลัพธ์โดยประมาณนี้มีความคลาดเคลื่อนมากเพียงใด ลองดูวิธีการนี้ในกรณีที่ง่ายที่สุด

191. การประมาณความขาดและส่วนเกินหากเราใช้ตัวเลขโดยประมาณแทนจำนวนที่แน่นอน เราจะเรียกค่าหลังนี้ เข้าใกล้ด้วยความเสียเปรียบหากน้อยกว่าจำนวนที่แน่นอน และหากเกินหากมากกว่านั้น ความแตกต่างระหว่างจำนวนที่แน่นอนและการประมาณนั้นเรียกว่าข้อผิดพลาดของการประมาณนี้ ตัวอย่างเช่น หากจำนวนที่แน่นอนคือ 3.826 และเราเอา 3.82 แทนตัวเลขนี้ นี่จะเป็นค่าประมาณที่มีข้อเสีย และข้อผิดพลาดคือ 0.006 หากเราใช้แทน 3.826 สมมติว่า 3.83 เราก็จะได้ค่าประมาณที่เกินมา และข้อผิดพลาดจะเป็น 0.004 โดยปกติแล้ว ยังไม่ทราบค่าที่แน่นอนของข้อผิดพลาด และทราบเพียงว่ามีค่าน้อยกว่าเศษส่วนที่กำหนด เช่น น้อยกว่า 1/100 แล้วเขาบอกว่าค่าประมาณสูงถึง 1/100 พอดี.

เช่น สมมุติว่า 2.85 เป็นการประมาณตัวเลข ก ด้วยความแม่นยำ 1/100 ซึ่งหมายความว่า 2.85 แปรผันจาก ก น้อยกว่า 1/100 ดังนั้นหาก 2.85 เป็นการประมาณที่มีข้อเสียแล้วเป็นจำนวนที่แน่นอน ก อยู่ระหว่าง 2.85 ถึง 2.86 และถ้า 2.85 เป็นการประมาณค่าที่เกินแล้ว ก อยู่ระหว่าง 2.85 ถึง 2.84 หากยังไม่รู้ว่าค่าประมาณ 2.85 จะขาดหรือเกิน และรู้เพียงว่าแม่นถึง 1/100 แล้วตัวเลขนั้น ก เราบอกได้แค่ว่ามันอยู่ระหว่าง 2.84 ถึง 2.86

ข้อผิดพลาดที่เราเพิ่งพูดถึงเรียกว่าข้อผิดพลาดสัมบูรณ์ ซึ่งตรงกันข้ามกับข้อผิดพลาดสัมพัทธ์ ซึ่งหมายถึงอัตราส่วนของข้อผิดพลาดสัมบูรณ์ต่อจำนวนที่แน่นอน ดังนั้น หากแทนที่จะเป็นเลข 3.826 ที่แน่นอน เราจะได้ค่าประมาณ 3.82 แทน ข้อผิดพลาดที่เกี่ยวข้องจะเป็น 0.006: 3.820 = 6:3826 = 0.001568... เช่น น้อยกว่า 0.002 ซึ่งหมายความว่าเมื่อหาค่าประมาณ 3.82 เราก็ลดลงไปน้อยกว่า 0.002 ของจำนวนที่แน่นอน

บางครั้งข้อผิดพลาดเชิงสัมพันธ์จะแสดงเป็นเปอร์เซ็นต์ของจำนวนที่แน่นอน กล่าวคือ ข้อผิดพลาดดังกล่าวระบุว่าข้อผิดพลาดนั้นน้อยกว่าหลายเปอร์เซ็นต์ของจำนวนที่แน่นอน ดังนั้น หากข้อผิดพลาดสัมพัทธ์น้อยกว่า 0.002 ของจำนวนที่แน่นอน แสดงว่ามีค่าน้อยกว่า 0.2% ของจำนวนนี้ เนื่องจาก

ในอนาคตเราจะพูดถึงเฉพาะข้อผิดพลาดที่สมบูรณ์เท่านั้น เรียกง่ายๆ ว่า "ข้อผิดพลาด"

192. การประมาณทศนิยมเมื่อต้องรับมือกับตัวเลขทศนิยม การประมาณค่าจะดำเนินการด้วยความแม่นยำสูงสุด 1/10, สูงสุด 1/100 ฯลฯ และถึงแม้จะมีความแม่นยำสูงสุด 1/2 ของหน่วยทศนิยมก็ตาม การประมาณดังกล่าวพบได้ตามกฎต่อไปนี้

ก)เพื่อให้ได้ค่าประมาณที่มีข้อเสียที่กำหนด เลขทศนิยม(ด้วยจำนวนตำแหน่งทศนิยมที่ จำกัด หรืออนันต์) ด้วยความแม่นยำของหน่วยทศนิยมหนึ่งหน่วยของหลักใด ๆ ก็เพียงพอที่จะทิ้งตัวเลขทั้งหมดทางด้านขวาของหน่วยที่แสดงหน่วยของหลักนี้

ดังนั้น ค่าประมาณที่มีข้อเสียของเลข 3.14159... ด้วยความแม่นยำ 1/100 คือ 3.14 เพราะเลขนี้น้อยกว่าค่าที่กำหนดและมีข้อผิดพลาดเท่ากับ 0.159... หนึ่งร้อย น้อยกว่าค่าหนึ่ง ทั้งร้อย

ข)หากต้องการรับการประมาณค่าที่เกินจากเลขทศนิยมที่กำหนดด้วยความแม่นยำของหน่วยทศนิยมหนึ่งหน่วยของหลักใด ๆ ก็เพียงพอที่จะทิ้งตัวเลขทั้งหมดในตัวเลขทางด้านขวาของตัวเลขที่แสดงหน่วยของหลักนี้และเพิ่มขึ้นด้วย 1 ตัวสุดท้ายของเลขท้ายที่เก็บไว้

ดังนั้น ค่าประมาณที่เกินจากตัวเลข 3.14159... ด้วยความแม่นยำ 0.001 คือ 3.142 เนื่องจากตัวเลขนี้มากกว่าค่านี้และมีข้อผิดพลาดน้อยกว่า 0.001

วี)เพื่อให้ได้ค่าประมาณของเลขทศนิยมที่กำหนดด้วยความแม่นยำ 1/2 ของหน่วยทศนิยมของหลักใดๆ ก็เพียงพอแล้ว โดยทำตามที่กล่าวไว้ในกฎข้อ 1 เพื่อเพิ่มจำนวนหลักสุดท้ายที่เก็บไว้อีก 1 หลัก ถ้า หลักแรกที่ถูกทิ้งคือ 5 หรือมากกว่า 5 (แล้วค่าประมาณจะเกิน) มิฉะนั้นก็ปล่อยไว้ไม่เปลี่ยนแปลง (แล้วค่าประมาณจะขาด)

ดังนั้นค่าประมาณ (ที่มีข้อเสีย) ของตัวเลข 3.14159... ด้วยความแม่นยำ 1/2 ในร้อยคือ 3.14 เนื่องจากข้อผิดพลาดน้อยกว่า 0.5 ในร้อย การประมาณตัวเลขเดียวกัน (ส่วนเกิน) ด้วยความแม่นยำ 1/2 พันคือ 3.142 เนื่องจากข้อผิดพลาดเท่ากับ (1-0.59) พันนั้นเห็นได้ชัดว่าน้อยกว่า 0.5 พัน

193. ข้อผิดพลาดในผลรวมโดยประมาณจากคุณสมบัติของการบวกเลขคณิต เรารู้ว่าถ้าเทอมใดลดลงหรือเพิ่มขึ้นตามจำนวนที่กำหนด ผลรวมก็จะลดลงหรือเพิ่มขึ้นตามจำนวนเดียวกัน ดังนั้นหากเงื่อนไขทั้งหมดถูกนำมาใช้โดยมีข้อบกพร่องหรือมีส่วนเกินทั้งหมดผลรวมในกรณีแรกจะเป็นไปตามข้อบกพร่องและในกรณีที่สอง - มีส่วนเกินและข้อผิดพลาดของผลรวมจะเท่ากับผลรวมของ ข้อผิดพลาดของข้อกำหนดทั้งหมด หากเกิดขึ้นว่าข้อกำหนดบางข้อมีข้อบกพร่องและข้อกำหนดอื่น ๆ มีส่วนเกิน ข้อผิดพลาดที่เกิดจากข้อกำหนดที่มีข้อบกพร่องจะครอบคลุมทั้งหมดหรือบางส่วนโดยข้อผิดพลาดตรงกันข้ามกับข้อกำหนดที่มีส่วนเกินและดังนั้นสุดท้าย ข้อผิดพลาดของผลรวมน้อยกว่าผลรวมของข้อผิดพลาดของข้อกำหนด นี่คือตัวอย่างบางส่วน:

ก)สมมติว่าเราต้องค้นหาผลรวม:

√2 + √3 + √5 = 1,4142 . . . + 1,7320 . . . + 2,2360 . . .

สมมติว่าในแต่ละเทอมเราจำกัดทศนิยมสามตำแหน่งหลังจุดทศนิยม:

เนื่องจากเราถือว่าเงื่อนไขทั้งหมดมีข้อเสีย ผลรวมก็จะมีข้อเสียเช่นกัน ข้อผิดพลาดของแต่ละเทอมน้อยกว่า 1/2 ในพัน ดังนั้นข้อผิดพลาดของผลรวม 5.382 จึงน้อยกว่า (1/2 + 1/2 + 1/2) ในพัน เช่น น้อยกว่า 1.5 พัน. หากเราละทิ้งเลข 2 ตัวสุดท้ายในจำนวน 5.382 เราจะลดผลรวมลงอีก 2 ในพัน และข้อผิดพลาดของหมายเลข 5.38 จะน้อยกว่าผลรวมของ 1.5 + 2 = 3.5 ในพัน ซึ่งในทางกลับกันจะน้อยกว่า 5 ในพัน เช่น น้อยกว่า 3/กรัมในร้อย ดังนั้น 5.38 จึงเป็นผลรวมโดยประมาณของคำศัพท์เหล่านี้ ถือว่ามีข้อบกพร่องและแม่นยำถึง 1/2 ในร้อย

จากนั้นข้อผิดพลาดของผลรวม 10.9005 จะน้อยกว่านี้ไม่ว่าในกรณีใด
1/2 + 1/2 + 1/2 + 1/2 + 1/2 = 2.5 หมื่น; ถ้าเราทิ้งเลขหลักสุดท้าย 5 ของผลรวมนี้ เราจะลดมันลง 5 หมื่น และข้อผิดพลาดจะน้อยกว่า 5 + 2.5 = 7.5 หมื่น ซึ่งน้อยกว่า 1 หมื่น นั่นคือ น้อยกว่าหนึ่งพัน. ดังนั้นจำนวน 10,900 จึงเป็นผลรวมโดยประมาณที่มีข้อเสีย (เนื่องจากการลดลง 5 หมื่นนั้นมากกว่าการเพิ่มขึ้นที่เป็นไปได้ 2.5 หมื่น) ซึ่งแม่นยำถึง 1 ในพัน

จากตัวอย่างเหล่านี้ เห็นได้ชัดเจนว่าหากเราต้องการหาผลรวมโดยประมาณที่แม่นยำถึงหนึ่งหน่วยของหลักบางหลัก เราก็ต้องใช้ทศนิยมในเทอมมากกว่าที่เราจำเป็นต้องมีในผลลัพธ์สุดท้าย (มากกว่า 1 หลักหากไม่มี มากกว่า 10 เทอม) ตัวอย่างเช่น คุณต้องหาผลรวมที่มีความแม่นยำเป็น 1 ในร้อย:

โปรดทราบว่าบางครั้งตัวเลขหลักสุดท้ายของผลรวมโดยประมาณควรเพิ่มขึ้น 1 ตัวอย่างเช่น สมมติว่าในตัวอย่างที่ให้ไว้ตอนนี้ ทศนิยมตำแหน่งที่สามของผลรวม 95.534 จะไม่ใช่ 4 แต่เป็น 9; แล้วทิ้งไปจะได้ผลรวม 95.53 เสียเปรียบ แม่นคือ 6+9 = 15 ในพัน ซึ่งเท่ากับ 1.5 ในร้อย หากเราเพิ่มทศนิยมตำแหน่งสุดท้ายขึ้น 1 คือเอาเลข 95.54 ออกมา ก็จะทำให้ค่าคลาดเคลื่อนลดลงไป 1 ร้อยอย่างเห็นได้ชัด ซึ่งตอนนี้จะน้อยกว่า 1 ร้อยแล้ว (แต่ยังไม่ทราบว่าผลรวมโดยประมาณจะเป็นอย่างไร) จะขาดหรือเกิน)

194. ข้อผิดพลาดของความแตกต่างโดยประมาณจากคุณสมบัติ การลบเลขคณิตเรารู้ว่าถ้าเราลดหรือเพิ่มค่า minuend ส่วนต่างก็จะลดลงหรือเพิ่มขึ้นด้วยจำนวนที่เท่ากัน ถ้าเราลดหรือเพิ่มสิ่งที่ถูกลบออกไป ผลต่างก็จะเพิ่มขึ้นหรือลดลงด้วยจำนวนที่เท่ากัน ซึ่งหมายความว่าหากข้อมูลทั้งสองสำหรับการลบตัวเลขมีข้อบกพร่องหรือทั้งสองอย่างมีมากเกินไป ความคลาดเคลื่อนของผลต่างจะเท่ากับผลต่างของข้อผิดพลาดของตัวเลขที่กำหนด ถ้าจำนวนที่กำหนดหนึ่งจำนวนมีข้อบกพร่องและอีกจำนวนหนึ่งมีส่วนเกิน ข้อผิดพลาดของความแตกต่างควรเท่ากับผลรวมของข้อผิดพลาดของตัวเลขที่กำหนด นี่คือตัวอย่างบางส่วน:

1) √3 - √2 = 1,73205 ... - 1,41421

สมมติว่าเราใช้ทศนิยมเพียง 3 ตำแหน่งหลังจุดทศนิยมในแต่ละตัวเลข:

เนื่องจากเราทำการประมาณทั้งสองด้วยความแม่นยำ 1/2 ในพัน ดังนั้นข้อผิดพลาดของตัวเลขคือ 0.318 เท่ากับความแตกต่างข้อผิดพลาดของตัวเลขเหล่านี้น้อยกว่า 1/2 ในพัน และยังไม่ทราบว่าความแตกต่างโดยประมาณจะเป็นข้อบกพร่องหรือส่วนเกิน (ไม่ทราบว่าการลดลงใดจะมากกว่า: อันที่ลดลงหรืออันที่ถูกลบ)

2) ให้ต้องหาผลต่างระหว่างเลขประมาณ 7.283-5.496 ตรงกับหลัก 1 ในพัน โดยไม่รู้ว่าขาดทั้งสองอย่างหรือเกินทั้งสองอย่าง หรือขาดทั้งสองอย่างและ อื่น ๆ ที่มีส่วนเกิน

ดังนั้นหากคุณต้องการค้นหาความแตกต่างระหว่างตัวเลขโดยประมาณที่กำหนดด้วยความแม่นยำหนึ่งหน่วยของหลักบางหลักจากนั้นในตัวเลขที่กำหนดคุณสามารถ จำกัด ตัวเองให้อยู่ในหน่วยของหลักนี้ได้โดยทิ้งตัวเลขที่ต่ำกว่าทั้งหมดหากรู้ว่าตัวเลขทั้งสองนั้น ขาดหรือทั้งสองอย่างเกิน; หากไม่ทราบจำนวนเหล่านี้คุณจะต้องใช้ตัวเลขมากกว่าที่คุณต้องการในผลลัพธ์หนึ่งหลักและทิ้งหลักสุดท้ายของผลลัพธ์

195. ข้อผิดพลาดของผลิตภัณฑ์โดยประมาณจากคุณสมบัติของการคูณเลขคณิต เรารู้ว่าถ้าตัวประกอบตัวใดตัวหนึ่งลดลงหรือเพิ่มขึ้นตามจำนวนใดๆ ผลคูณจะลดลงหรือเพิ่มขึ้นตามจำนวนนี้คูณด้วยตัวประกอบอื่น ดังนั้น ถ้าตัวประกอบตัวใดตัวหนึ่งเป็นจำนวนที่แน่นอน และอีกตัวเป็นจำนวนโดยประมาณแล้ว ข้อผิดพลาดของผลิตภัณฑ์เท่ากับข้อผิดพลาดของปัจจัยโดยประมาณคูณด้วยปัจจัยที่แน่นอน .

ตัวอย่าง. คำนวณ 2πR, ที่ไหน π = 3.1415926... และ ร= 2.4 ม.

การจำกัดตัวเองให้มีค่าประมาณของตัวเลข π ด้วยความแม่นยำสูงสุด 1/2 พัน (ส่วนเกิน) เราจะได้รับ:

2πR = 3,142 4,8 = 15,0816.

ข้อผิดพลาดน้อยกว่า 1/2 4.8 = 2.4 ในพัน และการประมาณจะมากเกินพอ โดยการทิ้งตัวเลขสองตัวสุดท้ายออกไป เช่น 16 หมื่น = 1.6 พัน เราจะลดผลลัพธ์ด้วยจำนวนที่เท่ากัน ซึ่งหมายความว่าผลลัพธ์ของตัวเลข 15.08 จะสูงถึง 2.4-1.6 = 0.8 ในพันซึ่งน้อยกว่า 1 ในพัน (ดังนั้นผลลัพธ์ของ 15.08 จึงแสดงได้ดีกว่าดังนี้: 15.080) อย่างไรก็ตาม ยังไม่ทราบว่าค่าประมาณ 15.08 จะเป็นส่วนเกินหรือขาด

เมื่อปัจจัยทั้งสองเป็นตัวเลขโดยประมาณ ข้อผิดพลาดของผลิตภัณฑ์สามารถกำหนดได้ดังนี้ อนุญาต ก และ ข จะมีการประมาณทั้งที่เอาเสียเปรียบและผิดพลาดอย่างแรกคือ α และอย่างที่สอง β .
จากนั้นตัวเลขที่แน่นอนจะเป็น + α และ ข + β . ลองหาความแตกต่างระหว่างผลิตภัณฑ์ที่แน่นอน ( + α ) (ข + β ) และปิด เกี่ยวกับ :

(+ α ) (ข +β ) - เกี่ยวกับ = เกี่ยวกับ + α ข + ก β + αβ - เกี่ยวกับ = α ข + ก β + αβ

ตั้งแต่ตัวเลข α และ β เล็กแล้วสินค้า αβ เล็กมากจนสามารถละเลยได้ (เช่น ถ้า α <0,001 и β < 0,001, то αβ < 0,000001). Тогда можно сказать, что погрешность приближенного произведения เกี่ยวกับ เท่ากับ α ข + ก β นั่นคือมันเท่ากัน ผลรวมของผลคูณของข้อผิดพลาดของแต่ละปัจจัยโดยประมาณด้วยอีกปัจจัยหนึ่ง หากนำทั้งสองปัจจัยมาเกิน ก็จะได้ตัวเลขที่แน่นอน เอ - α และ ข - β แล้ว

เกี่ยวกับ - (เอ - α ) (ข - β ) = เกี่ยวกับ - เกี่ยวกับ + α ข + ก β - αβ = α ข + β ก - αβ ,

หรือยังละเลยตัวเลข αβ ,

เกี่ยวกับ - (เอ - α ) (ข - β ) = α ข + β ก ,

นั่นคือข้อผิดพลาดของผลรวมโดยประมาณจะแสดงด้วยผลรวมเดียวกันกับที่เราพบก่อนหน้านี้

ลองใช้สิ่งนี้กับตัวอย่างต่อไปนี้:

√3 √2 = 1,73205 ... 1,41422 ...

จำกัดตัวเองให้มีทศนิยมสี่ตำแหน่ง ให้เราคูณการประมาณด้วยข้อเสีย ซึ่งมีความแม่นยำ 0.0001:

1,7320 1,4142 = 2,44939440.

เนื่องจากการประมาณแต่ละครั้งน้อยกว่า 2 ดังนั้นข้อผิดพลาดของผลิตภัณฑ์โดยประมาณที่พบจึงน้อยกว่า 0.0001 2 + 0.0001 2 เช่น น้อยกว่า 4 หมื่นและจะมีข้อเสีย หากในผลิตภัณฑ์นี้เราทิ้งตัวเลข 39440 เราจะลดจำนวนผลิตภัณฑ์ลงอีกให้น้อยกว่าสี่หมื่น จากนั้นเราจะได้ผลคูณ 2.449 ซึ่งตรงกับ 4 + 4 = 8 หมื่น ซึ่งน้อยกว่า 10 หมื่น = 1 ในพัน ซึ่งหมายความว่าผลคูณโดยประมาณของ 2.449 จะขาดและแม่นยำถึง 0.001

ในกรณีเฉพาะเจาะจง เมื่อเราพูดถึงตัวอย่างของเราเกี่ยวกับการคูณรากที่สอง เราจะสามารถหาผลคูณได้ง่ายขึ้น เช่นนี้: โดยที่ √3 √2 = √6 เราจะแยกรากที่สองโดยประมาณออกจาก 6 ด้วยความแม่นยำที่ต้องการ เมื่อหยั่งรากถึงหนึ่งในพัน เราจะได้ตัวเลข 2.419 เดิม ซึ่งเราได้รับข้างต้นด้วยวิธีที่ต่างออกไป

196. การคูณแบบย่อให้เราระบุวิธีการคูณแบบย่อดังต่อไปนี้ซึ่งช่วยให้คุณสามารถค้นหาผลิตภัณฑ์ได้อย่างรวดเร็วด้วยความแม่นยำที่กำหนดไว้ล่วงหน้า สมมติว่าเราต้องค้นหาผลิตภัณฑ์ที่มีความแม่นยำ 0.001:

314,159265358... 74,632543926 ...

ก่อนอื่นเราจะระบุว่าการคูณแบบย่อดำเนินการอย่างไร จากนั้นจึงอธิบายว่าเหตุใด

เราเซ็นชื่อหลักของตัวคูณใต้ตัวคูณเข้า ลำดับย้อนกลับจากขวาไปซ้ายเพื่อให้ตัวเลขของหน่วยอย่างง่ายอยู่ใต้ตัวเลขของตัวคูณซึ่งแสดงหน่วยที่เล็กกว่าหน่วยของตัวเลข 100 เท่าซึ่งแสดงความแม่นยำที่กำหนดคือในกรณีของเราภายใต้ตัวเลข 6 แสนส่วน : :

จากนั้นเราคูณตัวคูณด้วยแต่ละหลักของตัวคูณ โดยไม่สนใจตัวเลขของตัวคูณที่อยู่ทางด้านขวาของหลักของตัวคูณที่เราคูณอยู่ เราเซ็นชื่องานบางส่วนเหล่านี้ไว้ข้างใต้เพื่อให้ตัวเลขแรกทางด้านขวาอยู่ในคอลัมน์แนวตั้งเดียวกัน หลังจากนั้นเราจะรวมเข้าด้วยกัน ในตัวเลขผลลัพธ์เราจะละทิ้งตัวเลขสองตัวสุดท้ายและเพิ่มตัวเลขสุดท้ายของตัวเลขที่เหลืออีก 1 สุดท้าย เราใส่ลูกน้ำเพื่อให้หลักสุดท้ายแสดงหน่วยของหลักที่ต้องการ เช่น ในกรณีของเรา หนึ่งในพัน ผลลัพธ์หมายเลข 23446.505 จะมีความแม่นยำถึง 0.001 (ยังไม่ทราบแน่ชัด ต่ำกว่าหรือสูงกว่า)

ทีนี้มาอธิบายเทคนิคการคูณแบบย่อนี้กัน

ก่อนอื่น ให้เราตรวจสอบให้แน่ใจว่าผลิตภัณฑ์บางส่วนทั้งหมดแสดงหน่วยของหมวดหมู่เดียวกัน กล่าวคือหน่วยที่เล็กกว่า 100 เท่าของหมวดหมู่ที่กำหนด (ในตัวอย่างของเรา หนึ่งในแสนส่วน) ที่จริงแล้ว เมื่อคูณตัวเลข 314159265 ด้วยเลข 7 ตัวแรก เราจะคูณส่วนในล้านด้วยหลักสิบ ซึ่งหมายความว่าเราได้ส่วนหลักแสนในผลคูณ ต่อไป เมื่อคูณตัวเลข 31415926 ด้วย 4 เราก็คูณแสนด้วยหน่วยง่ายๆ ซึ่งหมายความว่าเราได้รับหนึ่งแสนในผลิตภัณฑ์อีกครั้ง ฯลฯ จากนี้ผลรวม 2344650499 แสดงถึงแสนคือหมายเลข 23446.50499 ให้เราแสดงว่าข้อผิดพลาดในผลลัพธ์สุดท้ายน้อยกว่า 0.001

เนื่องจากส่วนของตัวคูณที่เขียนทางด้านขวาของหมายเลข 7 ของตัวคูณนั้นน้อยกว่า 1 ในล้าน ดังนั้นหากละเลยผลคูณของส่วนนี้ด้วย 70 เราจึงลดผลลัพธ์ลงด้วยจำนวนที่น้อยกว่า 7 แสนส่วน นอกจากนี้เนื่องจากส่วนของตัวคูณที่เขียนทางด้านขวาของหมายเลข 4 ของตัวคูณนั้นน้อยกว่า 1 แสนส่วน ดังนั้นหากละเลยผลคูณของส่วนนี้ด้วย 4 หน่วยอย่างง่าย เราจึงลดผลลัพธ์ลงด้วยจำนวนที่น้อยกว่า 4 ร้อย หนึ่งในพัน การให้เหตุผลในลักษณะเดียวกันเกี่ยวกับตัวเลขอื่นๆ ทั้งหมดของตัวประกอบที่เราต้องคูณ เราสังเกตว่าเราลดผลลัพธ์ลงเป็นจำนวนที่น้อยกว่า 7 + 4 + 6 + + 3 + 2 + 5 + 4 + 3 + 9 ร้อย หนึ่งในพัน สุดท้าย เนื่องจากตัวคูณน้อยกว่า 1 พัน และส่วนของตัวประกอบที่เขียนทางด้านซ้ายของตัวคูณ (ซึ่งไม่จำเป็นต้องคูณเลย) จึงน้อยกว่า 2 + 1 ร้อยล้าน แล้วละเลย ผลคูณของตัวคูณด้วยปัจจัยส่วนนี้ เราจะลดผลลัพธ์ลงอีกเป็นจำนวนที่น้อยกว่า 2 + 1 แสนส่วน ดังนั้นการใช้หมายเลข 23446.50499 แทนที่จะเป็นผลิตภัณฑ์ที่แน่นอนเราจะลดจำนวนแรกลงด้วยจำนวนที่น้อยกว่า (7 + 4 + 6 + 3 + 2 + 5 + 4 + 3 + 9) + 2 +1 แสนส่วนนั่นคือ โดยทั่วไปจะน้อยกว่า กว่า 101 หนึ่งแสน เว้นแต่ผลรวมของหลักตัวคูณที่ต้องคูณเพิ่มขึ้นด้วยหลักแรกของหลักที่ทิ้งไปนั้นต้องไม่เกิน 100 (กรณีนี้กรณีจำนวนผลคูณบางส่วนไม่เกิน 101) 10) อีกทั้งทิ้งเลขท้ายสองตัวของผลลัพธ์เราก็ลดสินค้าลงอีกไม่เกิน 99 แสนส่วน ดังนั้นการลดลงทั้งหมดจะน้อยกว่า 101 + 99 แสนหรือน้อยกว่า 2 ในพัน ถ้าเราเพิ่มเลขหลักสุดท้ายขึ้น 1 คือ 1 ในพัน ผลลัพธ์ 23446.505 จะแตกต่างจากผลคูณที่แน่นอนน้อยกว่า 2-1 ในพัน นั่นคือ น้อยกว่าหนึ่งพัน (และยังไม่รู้ว่าจะเกินหรือขาด) .

โปรดทราบว่าไม่จำเป็นเสมอไปที่จะต้องเพิ่มหลักสุดท้ายของผลิตภัณฑ์ที่ถูกระงับไว้ 1 จะต้องดำเนินการตามตัวอย่างที่พิจารณา เนื่องจากมีข้อผิดพลาดของผลิตภัณฑ์ (ก่อนบวกเลขหลักสุดท้ายด้วย 1) น้อยกว่าผลรวม

(7 + 4 + 6 +3 + 2 + 5 + 4 + 3+ 9) + 2 + 1 + 99 แสน = 145 แสน

ซึ่งอยู่ระหว่าง 100 ถึง 200 แสนส่วน แต่หากทิ้ง 2 หลักไม่ใช่ 99 แต่ยกตัวอย่าง 25 แล้วข้อผิดพลาดของผลิตภัณฑ์จะน้อยกว่าผลรวม

(7 + 4 + 6 +3 + 2 + 5 + 4 + 3+ 9) + 2 + 1 + 25 แสน = 71 แสน

ซึ่งก็น้อยกว่าหนึ่งแสนหรือน้อยกว่าหนึ่งพันด้วย หมายความว่าไม่ต้องเพิ่มเลขท้าย 1 ในกรณีนี้สินค้าก็จะมีข้อเสีย

ความคิดเห็น ในการใช้กฎการคูณแบบย่อ เราไม่ได้สนใจตัวเลขของตัวคูณที่อยู่ทางขวาของตัวคูณ และไม่สนใจตัวเลขของตัวคูณที่อยู่ทางด้านซ้ายของตัวคูณ เราสามารถละทิ้งทั้งสองอย่างได้อย่างสมบูรณ์ ดังนั้นตัวคูณและตัวคูณของหลักที่ต้องการจะต้องมีจำนวนเท่ากัน การกำหนดล่วงหน้าได้ไม่ยากว่าต้องมีตัวเลขกี่หลักเพื่อให้สินค้ามีความแม่นยำตามที่กำหนด ลองอธิบายเรื่องนี้ด้วยตัวอย่าง สมมติว่าเราต้องคำนวณได้มากถึง 1/100 ผลิตภัณฑ์

1000π (√5 - 1),

ที่ไหน π คืออัตราส่วนของเส้นรอบวงต่อเส้นผ่านศูนย์กลาง เท่ากับ 3.1415926535... เมื่อให้ความสนใจกับการคูณครั้งล่าสุด เราให้เหตุผลดังนี้: ต้องคำนวณผลคูณที่ต้องการเป็นหนึ่งร้อย ซึ่งหมายความว่าตัวเลขหลักหน่วยของตัวคูณ (เช่น √5 - 1) จะต้องปรากฏใต้ทศนิยมตำแหน่งที่สี่ของตัวคูณ ในทางกลับกันในตัวคูณ (√5 - 1) ไม่มีหลักใดที่สูงกว่าหลักธรรมดา จากนี้เราสรุปได้ว่ามีทศนิยมมากกว่า 4 ตำแหน่งในตัวคูณ เช่น ใน 1,000 π มันไม่มีประโยชน์ที่จะคำนวณ แปลว่า 1,000 π ควรจะเท่ากับ 3141.5926; ดังนั้นในตัวคูณเช่นใน √5 - 1 จำเป็นต้องคำนวณ 8 หลัก โดยการสกัดเราจะพบว่า √5 =2.2360679 และด้วยเหตุนี้ √5 -1 = 1.2360679 การดำเนินการจะดำเนินการดังนี้:

197. ข้อผิดพลาดของผลหารโดยประมาณหากเงินปันผลเป็นตัวเลขโดยประมาณและตัวหารเป็นจำนวนที่แน่นอนแล้ว ความคลาดเคลื่อนของผลหารเท่ากับผลหารของความคลาดเคลื่อนของค่าประมาณหารด้วยตัวหารที่แน่นอน และผลหารโดยประมาณจะอยู่ที่ขาดหรือเกิน ขึ้นอยู่กับว่าเงินปันผลโดยประมาณจะถือว่าขาดหรือเกิน

ตัวอย่างเช่น ลองคำนวณผลหาร:

เราจำกัดการจ่ายเงินปันผลให้เป็นทศนิยมสามตำแหน่ง โดยคูณ:

0,538 7 = 3,766.

เราได้รับสินค้าที่มีข้อเสียที่แม่นยำถึง 1/2 7 = 3 1/2 ในพัน ดังนั้นผลหาร 3.766: 3 = 1.25533... ก็จะมีข้อเสียเช่นกัน และข้อผิดพลาดควรน้อยกว่า 3 1/2: 3 = 1 1/2 ในพัน หากผลหารผลลัพธ์เราทิ้งตัวเลขตามจำนวนหนึ่งในร้อยนั่นคือเราใช้เวลาเพียง 1.25 เราก็จะลดผลหารลงอีกอีกจำนวนน้อยกว่าหกในพัน ซึ่งหมายความว่าข้อผิดพลาดของหมายเลข 1.25 จะน้อยกว่า 6 +1 1/6 = 7 1/6 ในพัน ซึ่งน้อยกว่า 10 ในพัน นั่นคือ น้อยกว่า 1 ในร้อย

198. การหารแบบย่อ.เมื่อตัวหารเป็นตัวเลขโดยประมาณ และเงินปันผลเป็นค่าที่แน่นอนหรือประมาณการด้วย เป็นการยากที่จะระบุส่วนต่างของค่าคลาดเคลื่อนของผลหาร ในกรณีนี้ วิธีที่ดีที่สุดคือใช้วิธีการหารแบบย่อ ซึ่งช่วยให้คุณสามารถค้นหาผลหารได้อย่างรวดเร็วด้วยความแม่นยำที่กำหนดไว้ล่วงหน้า

เพื่อทำความเข้าใจทางลัดนี้ ก่อนอื่นเราต้องพิสูจน์ความจริงเสริมต่อไปนี้: ถ้าตัวหารเป็นจำนวนเต็มที่มีเศษส่วนและเราลบเศษส่วนนี้ออกจากตัวนั้น ผลหารจะเพิ่มขึ้นเป็นจำนวนที่น้อยกว่าผลหารนี้หารด้วยส่วนจำนวนเต็มของตัวหาร

ปล่อยให้เงินปันผลเป็น ก , ตัวแบ่ง ใน และเศษส่วนของตัวหาร α . แล้วส่วนจำนวนเต็มของตัวหารจะเท่ากับ ใน - α และผลหารที่แน่นอน = ก / บี , ผลหารโดยประมาณ = ก / บี-อัลฟ่า ความฉลาดเพิ่มขึ้น =

เพราะ α < 1, то อาฟ < ก ; จึงมีการเพิ่มขึ้นของเอกชน< ก / บี : (ใน - α ) กล่าวคือ น้อยกว่าผลหารหารด้วยส่วนจำนวนเต็มของตัวหาร สมมติว่าเราจำเป็นต้องค้นหาผลหารด้วยความแม่นยำ 0.01:

31 415,92653... : 432,639...

ก่อนอื่นเราจะระบุว่าการหารแบบย่อดำเนินการอย่างไร จากนั้นจึงอธิบายว่าทำไม

เรามาดูกันว่าผลหารโดยประมาณควรมีกี่หลัก เนื่องจากเงินปันผลมากกว่าตัวหารคูณด้วย 10 แต่น้อยกว่าตัวหารคูณด้วย 100 ดังนั้นส่วนจำนวนเต็มของผลหารจะต้องมี 2 หลัก เนื่องจากต้องคำนวณผลหารเป็นร้อย ตัวเลขทั้งหมดในผลหารโดยประมาณจึงต้องเป็น 4

ตอนนี้ให้เรานำเลข 4 นี้มาบวกเลขศูนย์ให้มากที่สุดเท่าที่จะเป็นไปได้ เราได้ 40,000. ทีนี้ลองแยกตัวเลขหลายๆ หลักในตัวหารทางด้านซ้าย (ไม่ต้องสนใจเครื่องหมายจุลภาค) เพื่อให้ได้ตัวเลขที่มากกว่า (หรือเท่ากับ) 40,000; แล้วตัวหารจะกลายเป็น 43,263. เราทิ้งหลักที่เหลือของตัวหาร. ในการจ่ายเงินปันผล เราใช้ตัวเลขทางซ้ายหลายหลัก (ไม่ต้องสนใจเครื่องหมายจุลภาค) เพื่อที่จะมีตัวหารที่สั้นลงในตัวเลขที่สร้างโดยพวกมัน (ไม่เกิน 9 ครั้ง) แล้วเงินปันผลจะเป็น 314,159 เราทิ้งหลักที่เหลือของเงินปันผล

เมื่อหารเงินปันผลนี้ด้วยตัวหาร เราจะพบตัวเลขตัวแรกของผลหาร 7 และส่วนที่เหลือตัวแรก 11,318 หลังจากนั้น เราขีดฆ่าตัวเลขหลักขวา 3 ตัวในตัวหาร และหารส่วนที่เหลือ 11318 ด้วยตัวเลขที่เหลือของตัวหาร 4326 เรา ได้หลักที่สองของผลหาร 2 และเศษที่สอง 2666 เราขีดฆ่าตัวหารอีกหนึ่งหลักทางขวาคือ 6 และหารเศษที่สองด้วย 432 เราได้หลักที่สามของผลหาร 6 และที่สาม เศษ 74 เราทำต่อไปต่อไป (ขีดฆ่าหนึ่งหลักทางขวาในตัวหารสำหรับแต่ละผลหาร) จนกว่าเราจะได้ตัวเลขทั้งหมดเป็นส่วนตัว ในที่สุด ในผลหารผลลัพธ์ เราวางลูกน้ำเพื่อให้ตัวเลขหลักสุดท้ายทางด้านขวาแสดงหน่วยของหลักที่ต้องการ (ในตัวอย่างของเรา หนึ่งในร้อย)

ให้เราอธิบายกระบวนการแบ่งแบบย่อนี้ ก่อนอื่น ให้เรานำคำถามในการหาผลหารไม่แม่นยำเท่ากับ 0.01 ตามความต้องการ แต่ต้องแม่นยำถึงทั้งหน่วย และตัวหารจะเป็นตัวเลขไม่น้อยกว่า 40,000 (กล่าวคือ จำนวนที่ หลักแรกและจำนวนศูนย์เท่ากับจำนวนหลักในผลหาร) ในการทำเช่นนี้ก็เพียงพอแล้ว: 1) เพิ่มเงินปันผล 100 เท่าซึ่งจะเพิ่มความฉลาดด้วยจำนวนเท่ากันและด้วยเหตุนี้จึงเกิดข้อผิดพลาด; 2) ย้ายเครื่องหมายจุลภาคในเงินปันผลและในตัวหารไปทางขวาด้วยจำนวนหลักเท่ากัน (ซึ่งจะไม่เปลี่ยนผลหาร) เพียงเท่านี้พอให้ตัวหารไม่ต่ำกว่า 40,000 ทีนี้คำถามก็ลดลงเหลือเพียงการหาว่า ผลหารที่แม่นยำถึงหนึ่ง:

314 159 265,3... : 43 203,9...

ลองทิ้งเศษส่วนในตัวหารออกไป จากนี้ ตามที่พิสูจน์แล้วข้างต้น เราจะเพิ่มผลหารด้วยจำนวนที่น้อยกว่าผลหารนี้หารด้วยส่วนจำนวนเต็มของตัวหาร แต่ผลหารที่มีทั้งหมด 4 หลัก น้อยกว่า 10,000 เราเอาตัวหารทั้งส่วนมากกว่า 40,000 แล้ว หมายความว่าเราจะเพิ่มความฉลาดขึ้นเป็นจำนวนน้อยกว่า 10,000: 40,000 เช่น น้อยกว่า 1/4 เมื่อคำนึงถึงสิ่งนี้ เราจะพบผลหาร:

314 159 265,3. . . : 43 263.

หากต้องการค้นหาหลักแรกของผลหาร ซึ่งก็คือ หลักพัน เราต้องหารจำนวนหลักพันของเงินปันผล (314159) ด้วยตัวหาร นี่คือสิ่งที่เราทำในการหารแบบย่อของเรา โดยได้หมายเลข 7 ส่วนที่เหลือของเงินปันผลที่แน่นอนจะเป็น 11,318,265.3... ส่วนที่เหลือนี้ต้องหารด้วย 43,263 เมื่อหารทั้งสองตัวเลขนี้ด้วย 10 เราจะนำคำถามมาสู่การหาร จาก 1131826.53. .. ที่ 4326.3 ผลหารนี้มีส่วนจำนวนเต็มเพียง 3 หลัก นี่หมายความว่ามันน้อยกว่า 1,000 หากทิ้งเศษส่วนในตัวหาร เราจะเพิ่มความฉลาดขึ้นอีกเป็นจำนวนที่น้อยกว่า 1,000: 4000 เช่น น้อยกว่า 1/4; เมื่อคำนึงถึงสิ่งนี้ เราจะหาผลหารได้
1,131,826.53...: 4326 หากต้องการหาหลักแรกของผลหารนี้ เช่น ร้อย คุณต้องหารจำนวนหลายร้อยของเงินปันผล (11,318) ด้วยตัวหาร (4320) นี่คือสิ่งที่เราทำในการหารแบบย่อ โดยได้เลขตัวที่สองเป็น 2 ในตัวหาร

เนื่องจากผลหารมี 4 หลัก เราจึงเพิ่มความฉลาดขึ้นน้อยกว่า 1 ในทางกลับกัน หากไม่หาร 31 ที่เหลือ... ด้วยตัวหาร 43 ตัวสุดท้าย เราจะลดผลหารลงน้อยกว่า 1 . ซึ่งหมายความว่าเราได้เพิ่มขึ้นน้อยกว่า 1 และลดลงน้อยกว่า 1; ดังนั้นผลลัพธ์จึงแม่นยำถึง 1 ไม่ว่าในกรณีใด

สิ่งที่เหลืออยู่ตอนนี้คือใส่ลูกน้ำในตำแหน่งที่เหมาะสม เราได้ 72.61 โดยมีความแม่นยำ 0.01

199. หมายเหตุกฎข้างต้นและคำอธิบายไม่จำเป็นต้องมีการเปลี่ยนแปลงใดๆ ในบางกรณี เมื่อเงินปันผลบางตัวมีตัวหารที่ตรงกัน 10 เท่า จากนั้นเราใส่เลข 10 ลงในผลหาร (ในวงเล็บ) จากการหารต่อไป เราจะเห็นว่าตัวเลขต่อไปนี้ทั้งหมดของผลหารต้องเป็นศูนย์ ตัวอย่างเช่น คุณต้องการหาผลหาร

485 172,923...: 78,254342...

แม่นยำถึง 1. ใช้กฎที่เราพบ

เงินปันผลครั้งที่สาม (7823) มีตัวหารที่สอดคล้องกัน (782) สิบครั้ง เราเขียนเลข 10 ในผลหาร ตัวเลขถัดไปในผลหารกลายเป็น 0 ผลหารที่ต้องการคือหมายเลข 61(10)0 เช่น 6200

ในกรณีนี้ ผลหารโดยประมาณจะมากกว่าผลหารที่แน่นอน อันที่จริง จำนวนผลหารที่พบก่อนโอกาสนี้จะต้องไม่น้อยกว่าที่ควรจะเป็น เนื่องจากในแต่ละผลหาร เราได้ตัวหารที่น้อยกว่าตัวหารที่แน่นอน ซึ่งหมายความว่าตัวเลขสองตัวแรกของผลหารที่แน่นอนจะต้องแสดงตัวเลขไม่เกิน 01 ดังนั้นจึงน้อยกว่า 6200

ตัวอย่างการใช้กฎก่อนหน้านี้คือปัญหาต่อไปนี้

200. ปัญหาคำนวณนิพจน์ต่อไปนี้ด้วยความแม่นยำ 1/100:

สำนวนนี้มีความเฉพาะเจาะจง ดังนั้นก่อนอื่น เราจะพิจารณาว่าควรมีตัวเลขจำนวนเท่าใดในผลหารนี้ และด้วยเหตุนี้ เราจำเป็นต้องรู้ตัวเลขสูงสุดของมัน
เมื่อเริ่มแยก √348 และ √127 เราจะเห็นว่ารูทแรกในส่วนทั้งหมดมี 18 และ 11 ตัวที่สอง ดังนั้นตัวเศษจะอยู่ที่ประมาณ 7 ตัวส่วนจะอยู่ที่ประมาณ 2 ซึ่งหมายความว่าอันดับสูงสุดของผลหารคือหน่วยเฉพาะ เนื่องจากต้องคำนวณผลหารเป็นร้อย จึงต้องมี 3 หลัก ดังนั้นเราจึงต้องคำนวณตัวส่วนอย่างแม่นยำจนเป็นไปได้ (ตามกฎของการหารแบบย่อ) เพื่อสร้างตัวเลขที่มากกว่า 3,000 ซึ่งเพียงพอที่จะคำนวณตัวเลข 5 หลักและด้วยเหตุนี้จึงจำเป็น (ตามกฎ ของการบวกแบบย่อ) เพื่อหารากของตัวส่วนที่มี 6 หลัก หลังจากแยกออกแล้วเราจะพบว่า:

√2 =1.41421; √3 = 1.73205; √5 =2.23606; √12 =3.46410 แล้ว:

√2 + √3 + √5 - √12 =1.9183 (สูงสุด 1/10000)

ตอนนี้เราต้องคำนวณตัวเศษด้วยความแม่นยำจนสามารถสร้างตัวเลขที่มากกว่า 19183 จากหลักแรกได้ เนื่องจากตัวเศษมีค่าประมาณ 7 ดังนั้นนอกเหนือจากจำนวนเต็มจึงจำเป็นต้องคำนวณทศนิยมอีก 4 ตำแหน่ง และเนื่องจากตัวเศษมีความแตกต่างกัน ดังนั้นค่า minuend และ subtrahend จึงต้องคำนวณเป็นทศนิยมตำแหน่งที่สี่ด้วย โดยการสกัดเราจะพบว่า:

√348 =18,6547; √127 = 11,2694; √348 - √127 = 7,3853.

ยังคงแบ่งตามกฎของการหารแบบย่อ 73,853 p.1 19,183 หลังจากนั้นเราจะได้รับ:

x = 3.85 (มากถึง 1/100)

บทที่สี่

การเปลี่ยนแปลงการแสดงออกที่ไม่ลงตัว

201. นิพจน์พีชคณิตที่มีเหตุผลและไม่มีเหตุผลนิพจน์พีชคณิตเรียกว่าเหตุผลโดยคำนึงถึงตัวอักษรใดๆ ที่รวมอยู่ในนิพจน์นี้ หากตัวอักษรนี้ไม่ปรากฏใต้เครื่องหมายกรณฑ์ มิฉะนั้นสำนวนนี้เรียกว่าไม่มีเหตุผลด้วยความเคารพต่อจดหมายฉบับนี้ ตัวอย่างเช่น การแสดงออก 3a +2 √x มีบางอย่างที่สมเหตุสมผลเกี่ยวกับ ก และค่อนข้างไร้เหตุผล เอ็กซ์ .

หากพวกเขาพูดว่า: "การแสดงออกทางพีชคณิตที่มีเหตุผล (หรือไม่มีเหตุผล)" โดยไม่เพิ่มสัมพันธ์กับตัวอักษรใด จะถือว่ามันเป็นเหตุผล (หรือไม่มีเหตุผล) ที่เกี่ยวข้องกับตัวอักษรทั้งหมดที่รวมอยู่ในการแสดงออก

202. คุณสมบัติหลักของหัวรุนแรงโปรดทราบว่าราก (ราก) ที่เราจะพูดถึงในบทนี้แน่นอนว่าเป็นเพียงเลขคณิตเท่านั้น ลองใช้คำที่ต่างไปจากเดิมอย่างสิ้นเชิง 3 √ ก และเพิ่มจำนวนรากให้ยกกำลังบางอย่าง เช่น ยกกำลังสอง ในเวลาเดียวกัน ลองคูณเลขชี้กำลังของรากด้วยเลขชี้กำลังของระดับที่เรายกจำนวนรากขึ้นไป เช่น ในกรณีของเรา ให้คูณด้วย 2 จากนั้นเราจะได้รากใหม่: 6 √ ก 2 . ขอให้เราพิสูจน์ว่าการดำเนินการทั้งสองนี้ไม่ได้เปลี่ยนค่าของราก

สมมติว่าเราคำนวณ 3 √ แล้ว ก และได้จำนวนหนึ่ง เอ็กซ์ . จากนั้นเราสามารถเขียนความเท่าเทียมกันได้:

เอ็กซ์ = 3 √ก และ x 3 = ก .

โดยการยกกำลังสองทั้งสองด้านของความเสมอภาคสุดท้าย เราจะได้:

(x3 ) 2 = ก 2 , เช่น. x6 = ก 2 .

จากความเท่าเทียมครั้งล่าสุดก็ชัดเจนว่า เอ็กซ์ = 6 √ก 2 .

ดังนั้นจำนวนเดียวกัน เอ็กซ์ เท่ากับ 3 √ ก และ 6 √ ก 2 เพราะฉะนั้น:

3 √ก = 6 √ก 2 .

ในทำนองเดียวกัน คุณสามารถตรวจสอบได้ว่า:

เลย ค่าของรากจะไม่เปลี่ยนแปลงถ้าเราเพิ่มนิพจน์ที่รุนแรงขึ้นในระดับหนึ่งและในเวลาเดียวกันก็คูณเลขชี้กำลังของรากด้วยดัชนีของระดับที่นิพจน์ที่รุนแรงถูกยกขึ้น

203. การเปลี่ยนแปลงบางประการของอนุมูล

ก) ค่ารากขององศาที่ต่างกันสามารถลดให้เหลือตัวชี้วัดเดียวกันได้ (เช่นเดียวกับเศษส่วนที่มีตัวส่วนต่างกันสามารถลดให้เหลือตัวส่วนเท่ากันได้) ในการทำเช่นนี้ ก็เพียงพอที่จะค้นหาตัวคูณร่วม (ควรเป็นค่าที่น้อยที่สุด) ของเลขชี้กำลังของอนุมูลทั้งหมด และคูณเลขชี้กำลังของอนุมูลแต่ละตัวด้วยปัจจัยเพิ่มเติมที่เกี่ยวข้อง ขณะเดียวกันก็เพิ่มนิพจน์รากแต่ละตัวให้อยู่ในระดับที่เหมาะสม

ตัวอย่าง.

√ขวาน ; 3 √ก 2 ; 6 √x

ผลคูณที่เล็กที่สุดของอนุมูลคือ 6; ปัจจัยเพิ่มเติมจะเป็น: สำหรับราก 3 แรก, สำหรับ 2 ที่สองและสำหรับ 1 ที่สาม จากนั้น

ข) ถ้านิพจน์รากเป็นกำลังที่เลขชี้กำลังมีตัวประกอบร่วมกับเลขชี้กำลังของราก เลขยกกำลังทั้งสองก็สามารถลดลงได้ด้วยตัวประกอบนี้

ตัวอย่าง.

วี)ถ้า นิพจน์รากเป็นผลคูณของกำลังหลายตัว โดยเลขชี้กำลังมีตัวประกอบร่วมเดียวกันกับเลขชี้กำลังของราก ดังนั้น เลขยกกำลังทั้งหมดสามารถลดลงได้ด้วยตัวประกอบนี้

ตัวอย่าง.

204. อนุมูลที่คล้ายกันรากที่คล้ายกันคือรากที่มีนิพจน์รากเหมือนกันและมีเลขชี้กำลังรากเหมือนกัน ตัวอย่างเช่น นิพจน์:

+3ก 3 √เอ็กซ์ซี และ -5b 3 √เอ็กซ์ซี

หากต้องการทราบว่าอนุมูลเหล่านี้คล้ายกันหรือไม่ คุณควรจัดรูปให้ง่ายขึ้นก่อน กล่าวคือ ถ้าเป็นไปได้:

1) ลบปัจจัยที่สามารถแยกรากออกจากภายใต้เครื่องหมายของราก (ส่วนที่ 6, บทที่ 6, § 169, a)

2) จะเป็นอิสระจากตัวส่วนของเศษส่วนภายใต้ราก (มาตรา 6 บทที่ 6, § 169, c)

3) ลดระดับของรากโดยลดตัวบ่งชี้ของรากและรากด้วยปัจจัยร่วมหากมี

ตัวอย่าง.

1) อนุมูล 3 √ 8ขวาน 3 และ 6 √ 64ก 2 ย 12 จะคล้ายกันถ้าเราทำให้มันง่ายขึ้น:

3 √8ขวาน 3 = 2x 3 √ก ; 6 √64ก 2 ปี 12 = 2ย 2 6 √ก 2 = 2ย 2 3 √ก

2) สามอนุมูล จะออกมาคล้ายกันถ้าเราปลดปล่อยตัวเองจากตัวส่วนภายใต้ราก:

205. การดำเนินการกับ monomials ที่ไม่มีเหตุผล

ก) การบวกและการลบหากต้องการบวกหรือลบ monomials ที่ไม่ลงตัว ให้เชื่อมต่อเครื่องหมายบวกหรือลบและตัดคำที่คล้ายกันออกหากปรากฏ

ตัวอย่าง.

ข) การคูณ เราเห็นมาก่อน (มาตรา 6 บทที่ 6, § 168) ว่าการดึงรากของผลิตภัณฑ์นั้นเพียงพอที่จะแยกออกจากแต่ละปัจจัยแยกกัน นั่นหมายความว่าตรงกันข้าม หากต้องการคูณรากหลายตัวในระดับเดียวกัน ก็เพียงพอที่จะคูณจำนวนรากนั้น ดังนั้น:

√ก √ข √c = √abc ; 3 √x 3 √ย = 3 √เอ็กซ์ซี

หากให้ค่ารากที่มีเลขชี้กำลังต่างกันสำหรับการคูณ ขั้นแรกให้ลดให้เหลือเลขชี้กำลังหนึ่งตัวก่อน

หากมีค่าสัมประสิทธิ์อยู่หน้าราก แสดงว่าคูณกัน

ตัวอย่าง.

วี)แผนก. เรารู้ว่าการแยกรากออกจาก drbby ก็เพียงพอที่จะแยกมันออกจากตัวเศษและตัวส่วนแยกกัน (ส่วนที่ 6 บทที่ 6, § 168, c) นั่นหมายถึงในทางกลับกัน:

เช่น., หากต้องการแยกรากด้วยเลขชี้กำลังเดียวกัน ก็เพียงพอที่จะหารจำนวนรากของพวกมัน

จากนี้ก็ชัดเจนว่า x = 6 √ก , และดังนั้นจึง

ตัวอย่าง.

สรุปปัจจัย 2x ภายใต้เครื่องหมายรากของระดับที่ 3 เราจะได้:

206 การดำเนินการกับพหุนามที่ไม่ลงตัวถูกสร้างขึ้นตามกฎเดียวกันกับที่ได้มาจากพหุนามเชิงตรรกยะ เช่น:

207. การปลดปล่อยตัวส่วนของเศษส่วนจากรากเมื่อคำนวณนิพจน์เศษส่วนที่ตัวส่วนมีราก การแปลงเศษส่วนก่อนจะเป็นประโยชน์เพื่อให้ตัวส่วนไม่มีราก ตัวอย่างเช่นคุณต้องคำนวณ:

เราสามารถคำนวณได้โดยตรงโดยใช้สูตรนี้หรือสร้างเหตุผลของตัวส่วนก่อนซึ่งเพียงพอที่จะคูณทั้งสองเทอมของเศษส่วนนี้ด้วยผลรวม √3 + √2:

สูตร (2) สะดวกในการคำนวณมากกว่าสูตร (1) อย่างแรกเพราะมันมีเพียง 3 การกระทำเท่านั้น ไม่ใช่ 4 เช่นเดียวกับสูตร (1) และอย่างที่สองเพราะเมื่อ ในการคำนวณ ซึ่งโดยความจำเป็นเท่านั้นที่สามารถทำได้ โดยประมาณ ข้อผิดพลาดของผลลัพธ์นั้นค่อนข้างง่ายโดยกำหนดโดยสูตร (2) ดังนั้น เมื่อหา √3 และ √2 ได้แม่นยำจนถึงครึ่งพัน เราจะได้:

x = 1,732 + 1,414 = 3,146.

ผลลัพธ์นี้แม่นยำถึง 1/2 + 1/2 พัน เช่น สูงถึง 1/1000

เราจะยกตัวอย่างง่ายๆ ของการปลดปล่อยตัวส่วนจากรากที่สองกัน

1) . คูณทั้งสองพจน์ของเศษส่วนด้วย √5

หากมีจำนวนประกอบทั้งหมดอยู่ใต้เครื่องหมายกรณฑ์ บางครั้งอาจเป็นประโยชน์ที่จะแยกย่อยให้เป็นตัวประกอบเฉพาะ เพื่อพิจารณาว่าขาดตัวประกอบใดจึงจะเป็นกำลังสองสมบูรณ์ จากนั้น ก็เพียงพอที่จะคูณทั้งสองเทอมของเศษส่วนด้วยรากที่สองของผลคูณของตัวประกอบที่หายไปเท่านั้น เช่น:

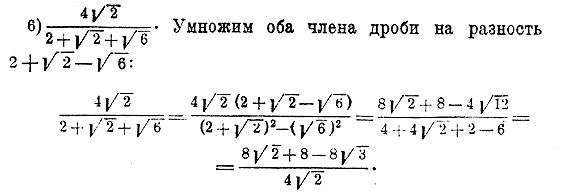
จากนั้นคูณทั้งสองพจน์ของเศษส่วนด้วย √2 เราจะได้:

______________