วิธีค้นหารากที่สองทางคณิตศาสตร์ของตัวเลข แยกรากออกจากเลขเศษส่วน

คณิตศาสตร์เกิดขึ้นเมื่อมนุษย์ตระหนักถึงตนเองและเริ่มวางตำแหน่งตนเองเป็นหน่วยอิสระของโลก ความปรารถนาที่จะวัด เปรียบเทียบ นับสิ่งที่อยู่รอบตัวคุณคือสิ่งที่เป็นรากฐานของวิทยาศาสตร์พื้นฐานประการหนึ่งในยุคของเรา ในตอนแรกสิ่งเหล่านี้เป็นอนุภาคของคณิตศาสตร์ระดับประถมศึกษาซึ่งทำให้สามารถเชื่อมโยงตัวเลขกับการแสดงออกทางกายภาพได้ต่อมาข้อสรุปเริ่มถูกนำเสนอในทางทฤษฎีเท่านั้น (เนื่องจากนามธรรม) แต่หลังจากนั้นไม่นานตามที่นักวิทยาศาสตร์คนหนึ่งกล่าวไว้ " คณิตศาสตร์ถึงจุดสูงสุดของความซับซ้อนเมื่อมันหายไปจากมัน” ตัวเลขทั้งหมด” แนวคิด " รากที่สอง“ปรากฏขึ้นในช่วงเวลาที่ข้อมูลเชิงประจักษ์สามารถรองรับได้อย่างง่ายดาย ซึ่งอยู่นอกเหนือระนาบของการคำนวณ

ที่ซึ่งทุกอย่างเริ่มต้นขึ้น

การกล่าวถึงรากครั้งแรกซึ่งก็คือ ช่วงเวลานี้แสดงว่า √ ได้รับการบันทึกไว้ในงานของนักคณิตศาสตร์ชาวบาบิโลนซึ่งเป็นผู้วางรากฐานสำหรับเลขคณิตสมัยใหม่ แน่นอนว่าพวกเขามีความคล้ายคลึงเล็กน้อยกับรูปแบบปัจจุบัน - นักวิทยาศาสตร์ในช่วงหลายปีที่ผ่านมาใช้แท็บเล็ตขนาดใหญ่เป็นครั้งแรก แต่ในสหัสวรรษที่สองก่อนคริสต์ศักราช จ. พวกเขาได้รับสูตรการคำนวณโดยประมาณที่แสดงวิธีแยกรากที่สอง ภาพด้านล่างแสดงหินที่นักวิทยาศาสตร์ชาวบาบิโลนแกะสลักกระบวนการอนุมาน √2 และปรากฏว่าถูกต้องมากจนพบความคลาดเคลื่อนในคำตอบในทศนิยมตำแหน่งที่สิบเท่านั้น

นอกจากนี้ รากยังถูกใช้หากจำเป็นต้องค้นหาด้านของสามเหลี่ยม โดยที่รู้อีกสองอัน เมื่อแก้สมการกำลังสอง ไม่มีทางหนีจากการแตกรากได้

นอกเหนือจากงานของชาวบาบิโลนแล้ว วัตถุประสงค์ของบทความนี้ยังได้รับการศึกษาในงานจีนเรื่อง "คณิตศาสตร์ในหนังสือเก้าเล่ม" และชาวกรีกโบราณได้ข้อสรุปว่าจำนวนใดก็ตามที่ไม่สามารถแยกรากออกมาได้โดยไม่มีเศษเหลือให้ผลลัพธ์ที่ไม่มีเหตุผล .

ต้นกำเนิดของคำนี้เกี่ยวข้องกับการแทนตัวเลขในภาษาอาหรับ: นักวิทยาศาสตร์โบราณเชื่อว่ากำลังสองของจำนวนตามใจชอบนั้นเติบโตจากรากเหมือนพืช ในภาษาละติน คำนี้ฟังดูเหมือน Radix (คุณสามารถติดตามรูปแบบได้ - ทุกสิ่งที่มีความหมายว่า "ราก" นั้นเป็นพยัญชนะ ไม่ว่าจะเป็นหัวไชเท้าหรือหัวไชเท้าอักเสบ)

นักวิทยาศาสตร์รุ่นต่อๆ มาหยิบยกแนวคิดนี้ขึ้นมา โดยกำหนดให้เป็น Rx ตัวอย่างเช่น ในศตวรรษที่ 15 เพื่อระบุว่ามีการใช้รากที่สองของจำนวนใดๆ a พวกเขาจึงเขียน R 2 a นิสัย มุมมองที่ทันสมัย"ติ๊ก" √ ปรากฏเฉพาะในศตวรรษที่ 17 ต้องขอบคุณ Rene Descartes

วันของเรา

ในแง่คณิตศาสตร์ รากที่สองของตัวเลข y คือตัวเลข z ซึ่งกำลังสองเท่ากับ y กล่าวอีกนัยหนึ่ง z 2 =y เทียบเท่ากับ √y=z อย่างไรก็ตาม คำจำกัดความนี้ที่เกี่ยวข้องเท่านั้นสำหรับ รากเลขคณิตเนื่องจากมันแสดงถึงค่าที่ไม่เป็นลบของนิพจน์ กล่าวอีกนัยหนึ่ง √y=z โดยที่ z มากกว่าหรือเท่ากับ 0

โดยทั่วไป ซึ่งใช้กับการหารากพีชคณิต ค่าของนิพจน์อาจเป็นค่าบวกหรือลบก็ได้ ดังนั้น เนื่องจากข้อเท็จจริงที่ว่า z 2 =y และ (-z) 2 =y เรามี: √y=±z หรือ √y=|z|

เนื่องจากความจริงที่ว่าความรักในคณิตศาสตร์เพิ่มขึ้นเมื่อมีการพัฒนาทางวิทยาศาสตร์เท่านั้นจึงมีอาการแสดงความรักต่อคณิตศาสตร์หลายอย่างที่ไม่ได้แสดงออกด้วยการคำนวณแบบแห้ง ตัวอย่างเช่น นอกเหนือจากปรากฏการณ์ที่น่าสนใจเช่นวันพายแล้ว ก็มีการเฉลิมฉลองวันหยุดรากที่สองด้วย มีการเฉลิมฉลองเก้าครั้งทุกๆ ร้อยปี และถูกกำหนดตามหลักการต่อไปนี้ ตัวเลขที่ระบุตามลำดับวันและเดือนจะต้องเป็นรากที่สองของปี ดังนั้นครั้งต่อไปที่เราจะเฉลิมฉลองวันหยุดนี้คือวันที่ 4 เมษายน 2016

คุณสมบัติของรากที่สองบนสนาม R

นิพจน์ทางคณิตศาสตร์เกือบทั้งหมดมีพื้นฐานทางเรขาคณิต และ √y ซึ่งถูกกำหนดให้เป็นด้านของสี่เหลี่ยมจัตุรัสที่มีพื้นที่ y ก็ไม่สามารถรอดพ้นชะตากรรมนี้ได้

จะหารากของตัวเลขได้อย่างไร?

มีอัลกอริธึมการคำนวณหลายอย่าง วิธีที่ง่ายที่สุด แต่ในขณะเดียวกันก็ค่อนข้างยุ่งยากคือการคำนวณทางคณิตศาสตร์ตามปกติซึ่งมีดังต่อไปนี้:

1) จากจำนวนที่เราต้องการรูท เลขคี่จะถูกลบออกตามลำดับ - จนกว่าส่วนที่เหลือที่เอาต์พุตจะน้อยกว่าจำนวนที่ถูกลบออกหรือแม้กระทั่งเท่ากับศูนย์ จำนวนการเคลื่อนไหวจะกลายเป็นจำนวนที่ต้องการในที่สุด เช่น คำนวณรากที่สองของ 25:

เลขคี่ถัดไปคือ 11 ส่วนที่เหลือคือ 1<11. Количество ходов - 5, так что корень из 25 равен 5. Вроде все легко и просто, но представьте, что придется вычислять из 18769?

ในกรณีเช่นนี้ จะมีการขยายซีรีส์ Taylor:

√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n โดยที่ n รับค่าตั้งแต่ 0 ถึง

+∞ และ |y|≤1

การแสดงกราฟของฟังก์ชัน z=√y

ลองพิจารณาฟังก์ชันพื้นฐาน z=√y บนสนามของจำนวนจริง R โดยที่ y มากกว่าหรือเท่ากับศูนย์ กำหนดการมีลักษณะดังนี้:

เส้นโค้งขยายจากจุดกำเนิดและจำเป็นต้องตัดกันจุด (1; 1)

คุณสมบัติของฟังก์ชัน z=√y บนสนามของจำนวนจริง R

1. ขอบเขตของคำจำกัดความของฟังก์ชันที่พิจารณาคือช่วงจากศูนย์ถึงบวกอนันต์ (รวมศูนย์ด้วย)

2. ช่วงของค่าของฟังก์ชันที่พิจารณาคือช่วงจากศูนย์ถึงบวกอนันต์ (รวมศูนย์อีกครั้ง)

3. ฟังก์ชันรับค่าต่ำสุด (0) ที่จุด (0; 0) เท่านั้น ไม่มีมูลค่าสูงสุด

4. ฟังก์ชัน z=√y ไม่เป็นคู่หรือคี่

5. ฟังก์ชัน z=√y ไม่ใช่คาบ

6. มีจุดตัดกันเพียงจุดเดียวของกราฟของฟังก์ชัน z=√y ที่มีแกนพิกัด: (0; 0)

7. จุดตัดของกราฟของฟังก์ชัน z=√y จะเป็นศูนย์ของฟังก์ชันนี้ด้วย

8. ฟังก์ชัน z=√y มีการเติบโตอย่างต่อเนื่อง

9. ฟังก์ชัน z=√y รับเฉพาะค่าบวก ดังนั้นกราฟจึงครองมุมพิกัดแรก

ตัวเลือกสำหรับการแสดงฟังก์ชัน z=√y

ในทางคณิตศาสตร์ เพื่ออำนวยความสะดวกในการคำนวณนิพจน์ที่ซับซ้อน บางครั้งจึงใช้รูปแบบกำลังของการเขียนรากที่สอง: √y=y 1/2 ตัวเลือกนี้สะดวก เช่น ในการเพิ่มฟังก์ชันเป็นกำลัง: (√y) 4 =(y 1/2) 4 =y 2 วิธีนี้ยังเป็นตัวแทนที่ดีในการหาอนุพันธ์ด้วยการอินทิเกรต เนื่องจากวิธีนี้ทำให้รากที่สองจึงแสดงเป็นฟังก์ชันยกกำลังธรรมดาได้

และในการเขียนโปรแกรม การแทนที่สัญลักษณ์ √ คือการรวมกันของตัวอักษร sqrt

เป็นที่น่าสังเกตว่าในพื้นที่นี้รากที่สองเป็นที่ต้องการอย่างมากเนื่องจากเป็นส่วนหนึ่งของสูตรเรขาคณิตส่วนใหญ่ที่จำเป็นสำหรับการคำนวณ อัลกอริธึมการนับนั้นค่อนข้างซับซ้อนและขึ้นอยู่กับการเรียกซ้ำ (ฟังก์ชันที่เรียกตัวเอง)

รากที่สองในสนามเชิงซ้อน C

โดยทั่วไปแล้ว มันเป็นหัวข้อของบทความนี้ที่กระตุ้นการค้นพบสนามของจำนวนเชิงซ้อน C เนื่องจากนักคณิตศาสตร์ถูกหลอกหลอนด้วยคำถามของการได้รากคู่ของจำนวนลบ นี่คือวิธีที่หน่วยจินตภาพที่ฉันปรากฏ ซึ่งมีคุณสมบัติที่น่าสนใจมาก นั่นคือกำลังสองของมันคือ -1 ด้วยเหตุนี้ สมการกำลังสองจึงถูกแก้ไขแม้จะมีการแบ่งแยกเชิงลบก็ตาม ใน C คุณสมบัติเดียวกันนี้เกี่ยวข้องกับรากที่สองเช่นเดียวกับใน R สิ่งเดียวคือข้อจำกัดเกี่ยวกับนิพจน์รากจะถูกลบออก

สรุปตัวเลข

รากที่สองที่ไม่เป็นลบของจำนวนบวกเรียกว่า รากที่สองทางคณิตศาสตร์และแสดงด้วยเครื่องหมายกรณฑ์

จำนวนเชิงซ้อน

ในสนามของจำนวนเชิงซ้อน มักจะมีคำตอบสองข้อเสมอ โดยต่างกันแค่เครื่องหมายเท่านั้น (ยกเว้นรากที่สองของศูนย์) รากของจำนวนเชิงซ้อนมักเขียนแทนด้วย แต่ต้องใช้สัญกรณ์นี้อย่างระมัดระวัง ข้อผิดพลาดทั่วไป:

หากต้องการแยกรากที่สองของจำนวนเชิงซ้อน จะสะดวกในการใช้รูปแบบเลขชี้กำลังในการเขียนจำนวนเชิงซ้อน: ถ้า

, ,

โดยที่เข้าใจรากของโมดูลัสในแง่ของค่าเลขคณิตและ k สามารถรับค่า k=0 และ k=1 ดังนั้นคำตอบจึงลงเอยด้วยผลลัพธ์ที่แตกต่างกันสองแบบ

ลักษณะทั่วไป

รากที่สองถูกนำมาใช้เป็นคำตอบของสมการของรูปแบบสำหรับวัตถุอื่น ๆ เช่น เมทริกซ์ ฟังก์ชัน ตัวดำเนินการ ฯลฯ การดำเนินการคูณแบบค่อนข้างอิสระสามารถใช้เป็นการดำเนินการได้ เช่น การซ้อน

สแควร์รูทในวิทยาการคอมพิวเตอร์

ในภาษาการเขียนโปรแกรมระดับฟังก์ชันหลายๆ ภาษา (เช่นเดียวกับภาษามาร์กอัป เช่น LaTeX) ฟังก์ชันรากที่สองจะถูกเขียนเป็น ตารางวา(จากอังกฤษ รากที่สอง"รากที่สอง").

อัลกอริทึมสำหรับการค้นหารากที่สอง

การค้นหาหรือการคำนวณรากที่สองของจำนวนที่กำหนดเรียกว่า การสกัด(รากที่สอง.

การขยายซีรีส์เทย์เลอร์

ที่ .

รากที่สองทางคณิตศาสตร์

สำหรับกำลังสองของตัวเลข ความเท่าเทียมกันต่อไปนี้จะเป็นจริง:

นั่นคือ คุณสามารถค้นหาส่วนจำนวนเต็มของรากที่สองของตัวเลขได้โดยการลบเลขคี่ทั้งหมดตามลำดับจนกระทั่งส่วนที่เหลือน้อยกว่าจำนวนที่ลบถัดไปหรือเท่ากับศูนย์ แล้วนับจำนวนการกระทำที่ทำ ตัวอย่างเช่นเช่นนี้:

เสร็จสิ้น 3 ขั้นตอน รากที่สองของ 9 คือ 3

ข้อเสียของวิธีนี้คือหากรากที่ถูกแยกออกมาไม่ใช่จำนวนเต็ม คุณจะสามารถค้นหาได้เฉพาะส่วนทั้งหมดเท่านั้น แต่ไม่แม่นยำกว่านี้ ในขณะเดียวกัน เด็ก ๆ ก็สามารถเข้าถึงวิธีนี้ได้ค่อนข้างมากซึ่งแก้ปัญหาทางคณิตศาสตร์ง่ายๆ ที่ต้องแยกรากที่สองออก

การประมาณคร่าวๆ

อัลกอริทึมมากมายสำหรับการคำนวณรากที่สองของจำนวนจริงบวก สต้องการค่าเริ่มต้นบางอย่าง หากค่าเริ่มต้นอยู่ไกลจากมูลค่าที่แท้จริงของรูทมากเกินไป การคำนวณจะช้าลง ดังนั้นจึงมีประโยชน์ในการประมาณค่าคร่าวๆ ซึ่งอาจไม่แม่นยำมากนัก แต่คำนวณได้ง่าย ถ้า ส≥ 1, เอาล่ะ ดีจะเป็นจำนวนหลัก สทางด้านซ้ายของจุดทศนิยม ถ้า ส < 1, пусть ดีจะเป็นจำนวนศูนย์ที่อยู่ติดกันทางด้านขวาของจุดทศนิยมโดยมีเครื่องหมายลบ จากนั้นการประมาณคร่าวๆ จะเป็นดังนี้:

ถ้า ดีแปลก, ดี = 2n+1 แล้วใช้ ถ้า ดีสม่ำเสมอ, ดี = 2n+2 แล้วใช้

มีการใช้สองและหกเพราะว่า และ

เมื่อทำงานในระบบไบนารี่ (เช่นเดียวกับภายในคอมพิวเตอร์) ควรใช้การประเมินที่แตกต่างออกไป (ที่นี่ ดีคือจำนวนเลขฐานสอง)

รากที่สองของเรขาคณิต

หากต้องการแตกรากด้วยตนเอง จะใช้สัญลักษณ์ที่คล้ายกับการหารยาว หมายเลขที่รากที่เรากำลังมองหาถูกเขียนลงไป ทางด้านขวาเราจะค่อยๆ ได้จำนวนรูทที่ต้องการ ลองหารากของตัวเลขที่มีทศนิยมจำนวนจำกัดกัน เริ่มต้นด้วยการแบ่งตัวเลข N ออกเป็นกลุ่มๆ ละ 2 หลักทางด้านซ้ายและทางขวาของจุดทศนิยม ไม่ว่าจะทางจิตใจหรือด้วยเครื่องหมายก็ตาม หากจำเป็น กลุ่มจะถูกเติมด้วยศูนย์ - ส่วนจำนวนเต็มจะถูกเติมทางด้านซ้าย และส่วนที่เป็นเศษส่วนทางด้านขวา ดังนั้น 31234.567 สามารถแสดงเป็น 03 12 34 ได้ 56 70. การรื้อถอนดำเนินการในกลุ่มตัวเลข 2 หลักซึ่งแตกต่างจากการแบ่ง

คำอธิบายภาพของอัลกอริทึม:

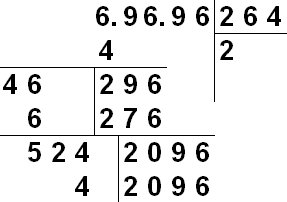
พื้นที่ที่ดินแปลงสี่เหลี่ยมคือ 81 dm² ค้นหาด้านของเขา สมมติว่าความยาวด้านของสี่เหลี่ยมจัตุรัสเท่ากับ เอ็กซ์เดซิเมตร จากนั้นพื้นที่ของแปลงคือ เอ็กซ์² ตารางเดซิเมตร เนื่องจากตามเงื่อนไข พื้นที่นี้เท่ากับ 81 dm² ดังนั้น เอ็กซ์² = 81 ความยาวของด้านของสี่เหลี่ยมจัตุรัสเป็นจำนวนบวก จำนวนบวกที่มีกำลังสองคือ 81 คือหมายเลข 9 เมื่อแก้ปัญหาจำเป็นต้องค้นหาตัวเลข x ซึ่งมีกำลังสองคือ 81 เช่น แก้สมการ เอ็กซ์² = 81 สมการนี้มีสองราก: x 1 = 9 และ x 2 = - 9 เนื่องจาก 9² = 81 และ (- 9)² = 81 ทั้งเลข 9 และ - 9 เรียกว่ารากที่สองของ 81

โปรดทราบว่ารากที่สองตัวใดตัวหนึ่ง เอ็กซ์= 9 เป็นจำนวนบวก มันถูกเรียกว่ารากที่สองทางคณิตศาสตร์ของ 81 และเขียนแทน √81 ดังนั้น √81 = 9

รากที่สองทางคณิตศาสตร์ของตัวเลข กเป็นจำนวนที่ไม่เป็นลบซึ่งมีกำลังสองเท่ากับ ก.

ตัวอย่างเช่น ตัวเลข 6 และ - 6 เป็นรากที่สองของตัวเลข 36 อย่างไรก็ตาม ตัวเลข 6 เป็นรากที่สองทางคณิตศาสตร์ของ 36 เนื่องจาก 6 เป็นจำนวนที่ไม่เป็นลบ และ 6² = 36 ตัวเลข - 6 ไม่ใช่ รากเลขคณิต

รากที่สองทางคณิตศาสตร์ของตัวเลข กแสดงดังต่อไปนี้: √ ก.

เครื่องหมายนี้เรียกว่าเครื่องหมายรากที่สองทางคณิตศาสตร์ ก- เรียกว่า สำนวนที่รุนแรง. นิพจน์ √ กอ่าน เช่นนี้: รากที่สองทางคณิตศาสตร์ของตัวเลข ก.ตัวอย่างเช่น √36 = 6, √0 = 0, √0.49 = 0.7 ในกรณีที่ชัดเจนว่าเรากำลังพูดถึงรากเลขคณิต พวกเขาพูดสั้น ๆ ว่า: "รากที่สองของ ก«.

การค้นหารากที่สองของตัวเลขเรียกว่าการรูทกำลังสอง การกระทำนี้จะตรงกันข้ามกับการยกกำลังสอง

คุณสามารถยกกำลังสองจำนวนใดก็ได้ แต่คุณไม่สามารถแยกรากที่สองออกจากจำนวนใดๆ ได้ ตัวอย่างเช่นเป็นไปไม่ได้ที่จะแยกรากที่สองของตัวเลข - 4 หากมีรากดังกล่าวอยู่ให้แสดงด้วยตัวอักษร เอ็กซ์เราจะได้ค่าเท่ากันที่ไม่ถูกต้อง x² = - 4 เนื่องจากมีจำนวนที่ไม่เป็นลบทางด้านซ้ายและจำนวนลบทางด้านขวา

นิพจน์ √ กมันสมเหตุสมผลก็ต่อเมื่อเท่านั้น ≥ 0. คำจำกัดความของรากที่สองสามารถเขียนสั้นๆ ได้ดังนี้: √ ≥ 0, (√ก)² = ก. ความเท่าเทียมกัน (√ ก)² = กถูกต้องสำหรับ ≥ 0. ดังนั้นเพื่อให้แน่ใจว่ารากที่สองของจำนวนที่ไม่เป็นลบ กเท่ากับ ขนั่นคือในความเป็นจริงแล้ว √ ก =ขคุณต้องตรวจสอบว่าตรงตามเงื่อนไขสองประการต่อไปนี้: ข ≥ 0, ข² = ก.

รากที่สองของเศษส่วน

มาคำนวณกัน โปรดทราบว่า √25 = 5, √36 = 6 และมาตรวจสอบว่ามีความเท่าเทียมกันหรือไม่

เพราะ และ แล้วความเท่าเทียมกันก็เป็นจริง ดังนั้น, .

ทฤษฎีบท:ถ้า ก≥ 0 และ ข> 0 นั่นคือรากของเศษส่วนเท่ากับรากของตัวเศษหารด้วยรากของตัวส่วน จำเป็นต้องพิสูจน์ว่า: และ .

ตั้งแต่ √ ก≥0 และ √ ข> 0 แล้ว

เรื่องคุณสมบัติของการยกเศษส่วนเป็นกำลังและนิยามของรากที่สอง ทฤษฎีบทได้รับการพิสูจน์แล้ว ลองดูตัวอย่างบางส่วน

คำนวณโดยใช้ทฤษฎีบทที่พิสูจน์แล้ว .

ตัวอย่างที่สอง: พิสูจน์สิ่งนั้น , ถ้า ก ≤ 0, ข < 0. .

อีกตัวอย่างหนึ่ง: คำนวณ .

.

การแปลงรากที่สอง

การลบตัวคูณออกจากใต้เครื่องหมายรูท ให้การแสดงออกได้รับ ถ้า ก≥ 0 และ ข≥ 0 จากนั้นใช้ทฤษฎีบทรากของผลิตภัณฑ์ที่เราสามารถเขียนได้:

การแปลงนี้เรียกว่าการลบตัวประกอบออกจากเครื่องหมายรูท ลองดูตัวอย่าง;

คำนวณได้ที่ เอ็กซ์= 2. การทดแทนโดยตรง เอ็กซ์= 2 ในนิพจน์รากทำให้เกิดการคำนวณที่ซับซ้อน การคำนวณเหล่านี้สามารถทำให้ง่ายขึ้นได้หากคุณลบปัจจัยออกจากใต้เครื่องหมายรากก่อน: เมื่อแทนค่า x = 2 เราจะได้:

ดังนั้น เมื่อลบตัวประกอบออกจากใต้เครื่องหมายราก นิพจน์รากจะแสดงในรูปแบบของผลคูณโดยที่ตัวประกอบตั้งแต่หนึ่งตัวขึ้นไปเป็นกำลังสองของจำนวนที่ไม่เป็นลบ จากนั้นใช้ทฤษฎีบทรากของผลิตภัณฑ์และหารากของแต่ละตัวประกอบ ลองพิจารณาตัวอย่าง: ลดความซับซ้อนของนิพจน์ A = √8 + √18 - 4√2 โดยการนำตัวประกอบในสองเทอมแรกออกจากใต้เครื่องหมายราก เราจะได้: ให้เราเน้นย้ำถึงความเท่าเทียมกันนั้น ใช้ได้เฉพาะเมื่อเท่านั้น ก≥ 0 และ ข≥ 0. ถ้า ก < 0, то .

นักเรียนมักจะถามเสมอว่า “ทำไมฉันไม่สามารถใช้เครื่องคิดเลขในการสอบคณิตศาสตร์ได้? วิธีแยกรากที่สองของตัวเลขโดยไม่ต้องใช้เครื่องคิดเลข? ลองตอบคำถามนี้กัน

จะแยกรากที่สองของตัวเลขโดยไม่ต้องใช้เครื่องคิดเลขได้อย่างไร?

การกระทำ รากที่สองผกผันกับการกระทำของกำลังสอง

√81= 9 9 2 =81

หากคุณหารากที่สองของจำนวนบวกแล้วยกกำลังสองผลลัพธ์ คุณจะได้จำนวนเดียวกัน

จากจำนวนเล็กๆ ที่เป็นกำลังสองของจำนวนธรรมชาติ เช่น 1, 4, 9, 16, 25, ..., 100 สามารถแยกรากที่สองออกมาทางวาจาได้ โดยปกติที่โรงเรียนพวกเขาจะสอนตารางกำลังสองของจำนวนธรรมชาติมากถึงยี่สิบ เมื่อรู้ตารางนี้แล้ว มันเป็นเรื่องง่ายที่จะแยกรากที่สองออกจากตัวเลข 121,144, 169, 196, 225, 256, 289, 324, 361, 400 จากตัวเลขที่มากกว่า 400 คุณสามารถแยกมันออกมาได้โดยใช้วิธีการเลือกโดยใช้เคล็ดลับบางประการ ลองมาดูวิธีนี้พร้อมตัวอย่าง

ตัวอย่าง: แยกรากของหมายเลข 676.

เราสังเกตว่า 20 2 = 400 และ 30 2 = 900 ซึ่งหมายถึง 20< √676 < 900.

กำลังสองที่แน่นอนของจำนวนธรรมชาติลงท้ายด้วย 0; 1; 4; 5; 6; 9.
หมายเลข 6 ถูกกำหนดโดย 4 2 และ 6 2
ซึ่งหมายความว่าหากรากถูกนำมาจาก 676 จะเป็น 24 หรือ 26

ยังคงต้องตรวจสอบ: 24 2 = 576, 26 2 = 676

คำตอบ: √676 = 26 .

มากกว่า ตัวอย่าง: √6889 .

ตั้งแต่ 80 2 = 6400 และ 90 2 = 8100 จากนั้น 80< √6889 < 90.
หมายเลข 9 กำหนดโดย 3 2 และ 7 2 จากนั้น √6889 จะเท่ากับ 83 หรือ 87

ตรวจสอบกัน: 83 2 = 6889

คำตอบ: √6889 = 83 .

หากคุณพบว่าการแก้ปัญหาโดยใช้วิธีการเลือกนั้นทำได้ยาก คุณสามารถแยกตัวประกอบนิพจน์รากได้

ตัวอย่างเช่น, หา √893025.

ลองแยกตัวประกอบตัวเลข 893025 จำไว้ว่าคุณทำตอนเกรด 6

เราได้: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945

มากกว่า ตัวอย่าง: √20736. ลองแยกตัวประกอบจำนวน 20736:

เราได้ √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144

แน่นอนว่าการแยกตัวประกอบต้องอาศัยความรู้เกี่ยวกับเครื่องหมายการหารลงตัวและทักษะการแยกตัวประกอบ

และสุดท้ายก็มี กฎการแยกรากที่สอง. มาทำความคุ้นเคยกับกฎนี้พร้อมตัวอย่าง

คำนวณ √279841.

หากต้องการแยกรากของจำนวนเต็มหลายหลัก ให้หารจากขวาไปซ้ายเป็นหน้าที่มี 2 หลัก (ขอบซ้ายสุดอาจมีหนึ่งหลัก) เราเขียนแบบนี้: 27'98'41

ในการหาเลขตัวแรกของราก (5) เราจะหารากที่สองของกำลังสองสมบูรณ์ที่ใหญ่ที่สุดที่อยู่ในหน้าแรกทางซ้าย (27)
จากนั้นกำลังสองของหลักแรกของราก (25) จะถูกลบออกจากหน้าแรกและหน้าถัดไป (98) จะถูกบวกเข้ากับผลต่าง (ลบออก)
ทางด้านซ้ายของผลลัพธ์ 298 เขียนเลขสองหลักของรูท (10) หารด้วยจำนวนสิบทั้งหมดของตัวเลขที่ได้รับก่อนหน้านี้ (29/2 data 2) ทดสอบผลหาร (102 ∙ 2 = 204 ไม่ควรเกิน 298) และเขียน (2) หลังหลักแรกของราก
จากนั้นผลหารผลลัพธ์ 204 จะถูกลบออกจาก 298 และขอบถัดไป (41) จะถูกบวกเข้ากับผลต่าง (94)
ทางด้านซ้ายของผลลัพธ์หมายเลข 9441 เขียนผลคูณสองเท่าของหลักราก (52 ∙2 = 104) หารจำนวนสิบทั้งหมดของตัวเลข 9441 (944/104 กลับไปยัง 9) ด้วยผลิตภัณฑ์นี้ ทดสอบ ผลหาร (1,049 ∙9 = 9441) ควรเป็น 9441 และจดไว้ (9) หลังหลักที่สองของราก

เราได้รับคำตอบ √279841 = 529

สกัดในลักษณะเดียวกัน รากของเศษส่วนทศนิยม. เฉพาะจำนวนรากเท่านั้นที่ต้องแบ่งออกเป็นหน้าเพื่อให้ลูกน้ำอยู่ระหว่างหน้า

ตัวอย่าง. ค้นหาค่า √0.00956484

คุณเพียงแค่ต้องจำไว้ว่าถ้า ทศนิยมมีทศนิยมเป็นจำนวนคี่ จึงไม่สามารถแยกรากที่สองออกมาได้แน่ชัด

ตอนนี้คุณได้เห็นสามวิธีในการแยกรากแล้ว เลือกอันที่เหมาะกับคุณที่สุดแล้วฝึกฝน หากต้องการเรียนรู้ที่จะแก้ปัญหา คุณต้องแก้ปัญหาเหล่านั้น และหากคุณมีคำถามใดๆ ลงทะเบียนบทเรียนของฉันได้เลย

เว็บไซต์ เมื่อคัดลอกเนื้อหาทั้งหมดหรือบางส่วน จำเป็นต้องมีลิงก์ไปยังแหล่งที่มา

บ่อยครั้งเมื่อแก้ไขปัญหาเราต้องเผชิญกับปัญหาจำนวนมากซึ่งเราต้องแยกออกมา รากที่สอง. นักเรียนหลายคนตัดสินใจว่านี่เป็นข้อผิดพลาดและเริ่มแก้ไขตัวอย่างทั้งหมดใหม่ ไม่ควรทำเช่นนี้ไม่ว่าในกรณีใด! มีสองเหตุผลสำหรับสิ่งนี้:

1. รากจำนวนมากมักปรากฏอยู่ในปัญหา โดยเฉพาะในข้อความ
2. มีอัลกอริธึมที่ใช้คำนวณรากเหล่านี้เกือบจะเป็นปากเปล่า

เราจะพิจารณาอัลกอริทึมนี้ในวันนี้ บางทีบางสิ่งอาจดูไม่เข้าใจสำหรับคุณ แต่ถ้าคุณใส่ใจกับบทเรียนนี้ คุณจะได้ อาวุธที่ทรงพลังที่สุดขัดต่อ รากที่สอง.

ดังนั้นอัลกอริทึม:

1. จำกัดรากที่ต้องการด้านบนและด้านล่างให้เป็นตัวเลขที่ทวีคูณของ 10 ดังนั้น เราจะลดช่วงการค้นหาลงเหลือ 10 หมายเลข
2. จากตัวเลขทั้ง 10 นี้ ให้กำจัดสิ่งที่ไม่สามารถหยั่งรากได้อย่างแน่นอน เป็นผลให้ตัวเลข 1-2 จะยังคงอยู่
3. ยกกำลังสองตัวเลข 1-2 นี้ ผู้ที่มีกำลังสองเท่ากับตัวเลขเดิมจะเป็นราก

ก่อนที่จะนำอัลกอริทึมนี้ไปปฏิบัติ มาดูแต่ละขั้นตอนกันก่อน

ข้อจำกัดของรูท

ก่อนอื่น เราต้องค้นหาก่อนว่ารูทของเราอยู่ระหว่างเลขใด เป็นที่พึงปรารถนาอย่างยิ่งที่ตัวเลขจะเป็นทวีคูณของสิบ:

10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.

เราได้รับชุดตัวเลข:

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

ตัวเลขเหล่านี้บอกอะไรเรา? ง่ายมาก: เรามีขอบเขต ตัวอย่างเช่น หมายเลข 1296 อยู่ระหว่าง 900 ถึง 1600 ดังนั้นรากของมันต้องไม่น้อยกว่า 30 และมากกว่า 40:

[คำบรรยายภาพ]

เช่นเดียวกับตัวเลขอื่นๆ ที่ใช้หารากที่สองได้ ตัวอย่างเช่น 3364:

[คำบรรยายภาพ]

ดังนั้น แทนที่จะเป็นตัวเลขที่ไม่สามารถเข้าใจได้ เราจะได้ช่วงที่เฉพาะเจาะจงมากซึ่งมีรากดั้งเดิมอยู่ หากต้องการจำกัดพื้นที่การค้นหาให้แคบลง ให้ไปยังขั้นตอนที่สอง

กำจัดตัวเลขที่ไม่จำเป็นอย่างเห็นได้ชัด

เรามีตัวเลข 10 ตัว - ตัวเลือกสำหรับรูท เราได้มันมาเร็วมาก โดยไม่ต้องคิดที่ซับซ้อนและการคูณในคอลัมน์เดียว ได้เวลาไปต่อแล้ว.

เชื่อหรือไม่ว่า ตอนนี้เราจะลดจำนวนผู้สมัครลงเหลือ 2 คน - อีกครั้งโดยไม่มีการคำนวณที่ซับซ้อนใดๆ! ก็เพียงพอที่จะรู้กฎพิเศษ นี่คือ:

หลักสุดท้ายของสี่เหลี่ยมจะขึ้นอยู่กับหลักสุดท้ายเท่านั้น หมายเลขเดิม.

กล่าวอีกนัยหนึ่ง เพียงดูที่หลักสุดท้ายของสี่เหลี่ยมแล้วเราจะเข้าใจทันทีว่าตัวเลขเดิมสิ้นสุดที่ใด

มีเพียง 10 หลักเท่านั้นที่จะมาอยู่อันดับสุดท้ายได้ ลองหาดูว่าพวกมันกลายเป็นอะไรเมื่อยกกำลังสอง ลองดูที่ตาราง:

1	2	3	4	5	6	7	8	9	0
1	4	9	6	5	6	9	4	1	0

ตารางนี้เป็นอีกขั้นตอนหนึ่งในการคำนวณรูท อย่างที่คุณเห็น ตัวเลขในบรรทัดที่สองกลายเป็นสมมาตรสัมพันธ์กับทั้งห้า ตัวอย่างเช่น:

2 2 = 4;
8 2 = 64 → 4.

อย่างที่คุณเห็นตัวเลขหลักสุดท้ายจะเหมือนกันในทั้งสองกรณี ซึ่งหมายความว่า ตัวอย่างเช่น รากของ 3364 จะต้องลงท้ายด้วย 2 หรือ 8 ในทางกลับกัน เราจำข้อจำกัดจากย่อหน้าก่อนหน้าได้ เราได้รับ:

[คำบรรยายภาพ]

สี่เหลี่ยมสีแดงแสดงว่าเรายังไม่ทราบตัวเลขนี้ แต่รากอยู่ในช่วง 50 ถึง 60 ซึ่งมีเพียงตัวเลขสองตัวที่ลงท้ายด้วย 2 และ 8:

[คำบรรยายภาพ]

นั่นคือทั้งหมด! จากรากที่เป็นไปได้ทั้งหมด เราเหลือเพียงสองทางเลือกเท่านั้น! และนี่คือในกรณีที่ยากที่สุด เพราะหลักสุดท้ายอาจเป็น 5 หรือ 0 แล้วจะมีผู้สมัครเพียงคนเดียวเท่านั้นที่จะเป็นราก!

การคำนวณขั้นสุดท้าย

ดังนั้นเราจึงเหลือหมายเลขผู้สมัคร 2 ตัว. จะรู้ได้อย่างไรว่าอันไหนคือต้นตอ? คำตอบนั้นชัดเจน: ยกกำลังสองตัวเลขทั้งสอง ตัวที่ยกกำลังสองให้ตัวเลขเดิมจะเป็นราก

ตัวอย่างเช่น สำหรับหมายเลข 3364 เราพบหมายเลขที่เป็นตัวเลือกสองตัว: 52 และ 58 ลองยกกำลังสองกัน:

52 2 = (50 +2) 2 = 2500 + 2 50 2 + 4 = 2704;
58 2 = (60 - 2) 2 = 3600 - 2 60 2 + 4 = 3364

นั่นคือทั้งหมด! ปรากฎว่ารูตอยู่ที่ 58! ในเวลาเดียวกัน เพื่อให้การคำนวณง่ายขึ้น ฉันใช้สูตรกำลังสองของผลรวมและผลต่าง ด้วยเหตุนี้ ฉันจึงไม่ต้องคูณตัวเลขลงในคอลัมน์ด้วยซ้ำ! นี่เป็นอีกระดับของการเพิ่มประสิทธิภาพการคำนวณ แต่แน่นอนว่านี่เป็นทางเลือกโดยสมบูรณ์ :)

ตัวอย่างการคำนวณราก

แน่นอนว่าทฤษฎีก็ดี แต่ลองตรวจสอบในทางปฏิบัติ

[คำบรรยายภาพ]

ก่อนอื่นเรามาดูกันว่าหมายเลข 576 อยู่ระหว่างหมายเลขใด:

400 < 576 < 900
20 2 < 576 < 30 2

ทีนี้มาดูตัวเลขสุดท้ายกัน เท่ากับ 6. สิ่งนี้เกิดขึ้นเมื่อใด? เฉพาะในกรณีที่รากลงท้ายด้วย 4 หรือ 6 เราได้ตัวเลขสองตัว:

สิ่งที่เหลืออยู่คือการยกกำลังสองแต่ละหมายเลขแล้วเปรียบเทียบกับตัวเลขดั้งเดิม:

24 2 = (20 + 4) 2 = 576

ยอดเยี่ยม! สี่เหลี่ยมแรกกลายเป็นเลขเดิม นี่คือราก

งาน. คำนวณรากที่สอง:

[คำบรรยายภาพ]

900 < 1369 < 1600;
30 2 < 1369 < 40 2;

ลองดูที่หลักสุดท้าย:

1369 → 9;
33; 37.

ยกกำลังสอง:

33 2 = (30 + 3) 2 = 900 + 2 30 3 + 9 = 1,089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 40 3 + 9 = 1369

นี่คือคำตอบ: 37.

งาน. คำนวณรากที่สอง:

[คำบรรยายภาพ]

เราจำกัดจำนวน:

2500 < 2704 < 3600;
50 2 < 2704 < 60 2;

ลองดูที่หลักสุดท้าย:

2704 → 4;
52; 58.

ยกกำลังสอง:

52 2 = (50 + 2) 2 = 2500 + 2 50 2 + 4 = 2704;

เราได้รับคำตอบ: 52 ไม่จำเป็นต้องยกกำลังสองอีกต่อไป

งาน. คำนวณรากที่สอง:

[คำบรรยายภาพ]

เราจำกัดจำนวน:

3600 < 4225 < 4900;
60 2 < 4225 < 70 2;

ลองดูที่หลักสุดท้าย:

4225 → 5;
65.

อย่างที่คุณเห็นหลังจากขั้นตอนที่สองเหลือเพียงตัวเลือกเดียว: 65 นี่คือรูทที่ต้องการ แต่เรายังคงยกกำลังสองและตรวจสอบ:

65 2 = (60 + 5) 2 = 3600 + 2 60 5 + 25 = 4225;

ทุกอย่างถูกต้อง เราเขียนคำตอบ

บทสรุป

อนิจจาไม่ดีกว่า มาดูสาเหตุกัน มีสองคน:

• ในการสอบคณิตศาสตร์ทั่วไป ไม่ว่าจะเป็นการสอบ State หรือ Unified State Exam ห้ามใช้เครื่องคิดเลข และถ้าคุณนำเครื่องคิดเลขมาเรียน คุณจะถูกไล่ออกจากข้อสอบได้ง่ายๆ
• อย่าเป็นเหมือนคนอเมริกันโง่ ๆ ซึ่งไม่ใช่แค่ราก - มีสองอย่าง จำนวนเฉพาะพวกเขาไม่สามารถพับมันได้ และเมื่อพวกเขาเห็นเศษส่วน พวกเขามักจะมีอาการวิตกกังวล